在上一篇文章中,我們討論了失調誤差如何影響單極性 ADC 的傳遞函數(shù)。考慮到這一點,單極 ADC 的輸入只能接受正電壓。相比之下,雙極 ADC 的輸入可以處理正電壓和負電壓。在本文中,我們將探討雙極性和差分 ADC 中的失調和增益誤差規(guī)范;并了解失調誤差的單點校準。
傳遞函數(shù)——雙極 ADC 理想特性曲線
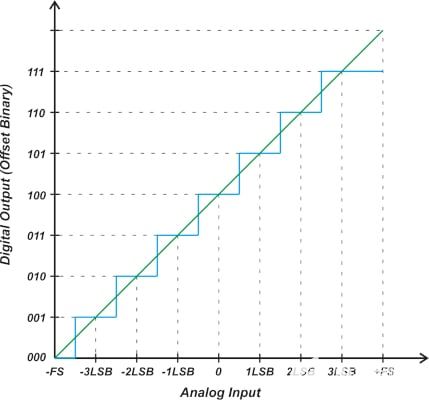
具有偏移二進制輸出編碼方案的理想三位 ADC 的傳遞函數(shù)如圖 1 所示。
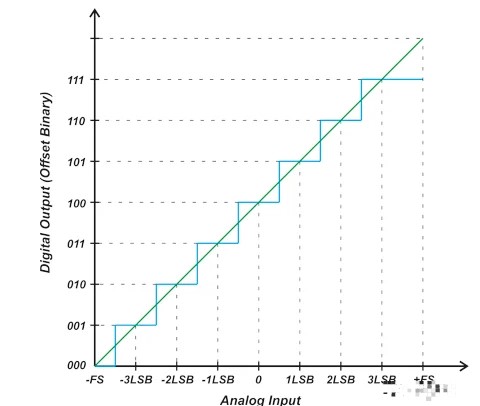
圖 1. 具有偏移二進制輸出編碼的理想三位 ADC 的傳遞函數(shù),
作為復習,對于偏移二進制系統(tǒng),中間刻度代碼的中心(在我們的示例中為 100)對應于 0 V 輸入。低于 100 的代碼表示負輸入電壓,高于 100 的數(shù)字值對應于正模擬輸入。但請注意,縱軸上的代碼順序與單極 ADC 的代碼順序完全相同。穿過臺階中點的直線為我們提供了 ADC 階梯響應的線性模型。
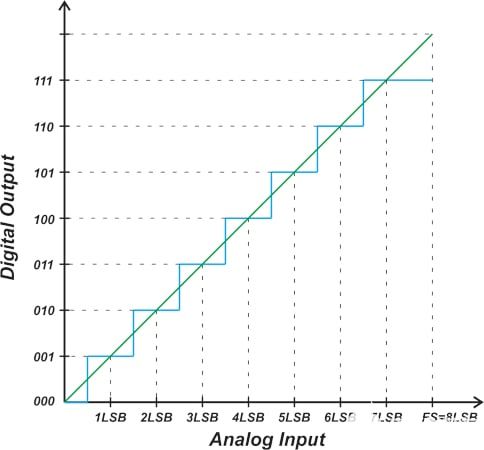
要注意的另一件事是,上述特性曲線也可以表示具有差分輸入的單極 ADC。由于低于 100 的輸出代碼表示負值,因此繪制上述傳遞函數(shù)很有幫助,如圖 2 所示。
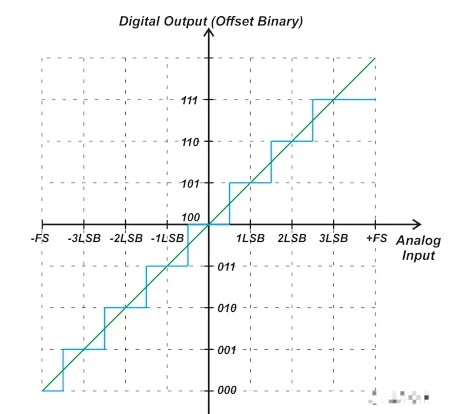
圖 2. 顯示低于 100 的輸出代碼的傳遞函數(shù)。
雙極 ADC 失調誤差
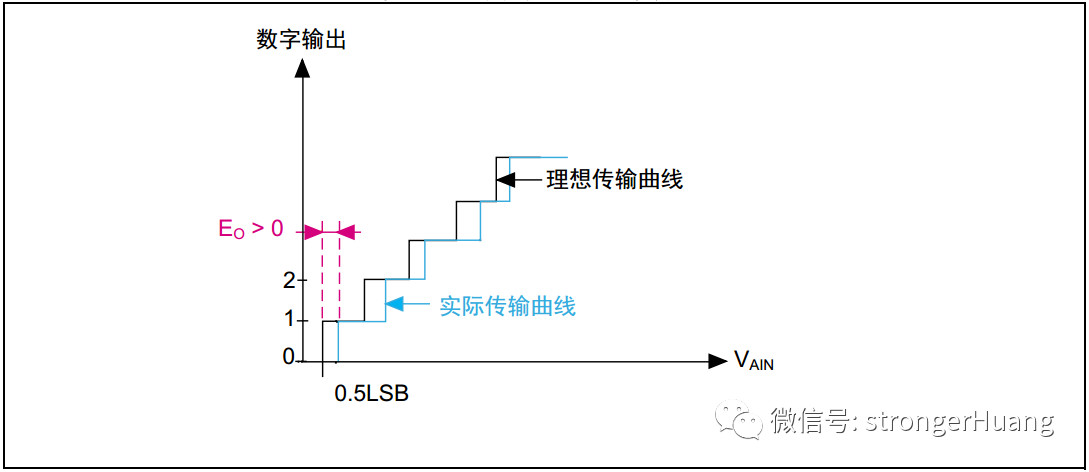
對于具有偏移二進制編碼方案的 ADC,偏移誤差可以通過比較從 100…00 到 100…01 的實際中間量程轉換與理想 ADC 中的相應轉換來找到。如圖 2 所示,這種轉換在理想情況下應該發(fā)生在 +0.5 LSB。圖 3 顯示了一個偏移值為 -1 LSB 的三位雙極性 ADC。
請注意,從 100 到 101 的中檔轉換發(fā)生在 +1.5 LSB 而不是 +0.5 LSB。
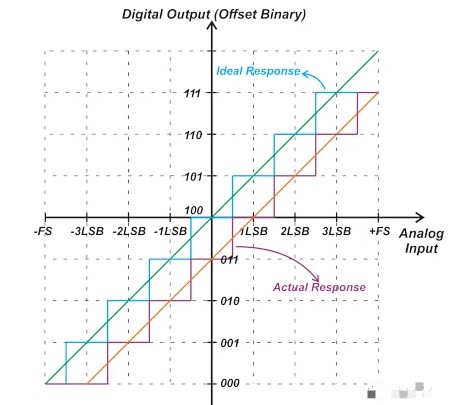
圖 3.偏移值為 -1 LSB 的三位雙極 ADC 的傳遞函數(shù)。
圖 4 顯示了具有正偏移的三位雙極性 ADC。
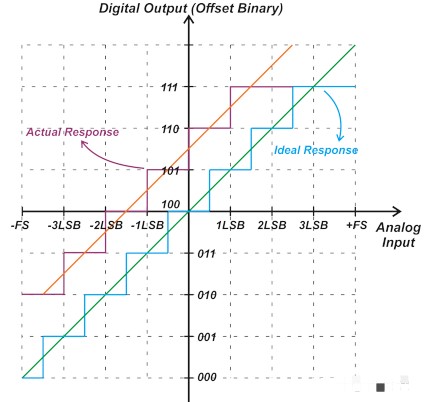
圖 4. 具有正偏移的三位雙極性 ADC。
在這種情況下,正輸入的第一次轉換發(fā)生在從 110 到 111 的 +1 LSB 處。對于理想的 ADC,該轉換應該發(fā)生在 +2.5 LSB 處。因此,實際傳遞函數(shù)的偏移量為 +1.5 LSB。您還可以通過檢查圖 4 中橙色直線所示的實際傳遞曲線的線性模型來獲得相同的結果。
雙極 ADC 增益誤差
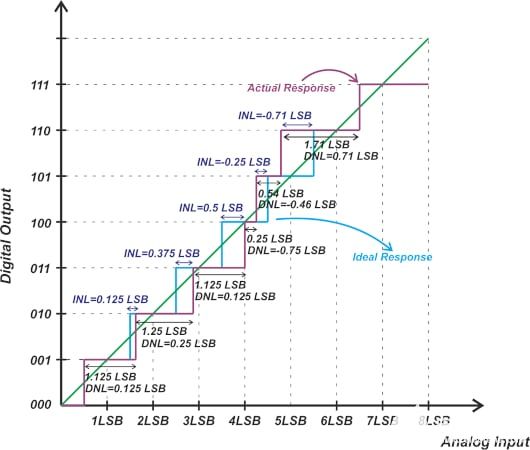
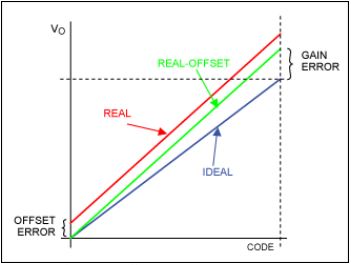
與單極 ADC 類似,雙極 ADC 的增益誤差可以定義為在消除失調誤差后實際最后一次轉換與理想最后一次轉換的偏差。增益誤差也可以定義為實際線性模型的斜率與理想直線模型的斜率的偏差。
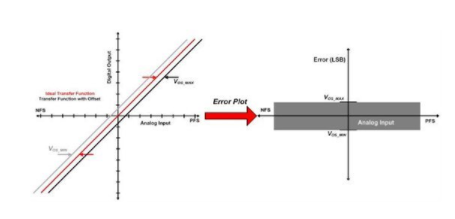
例如,考慮圖 5 所示的特性曲線。
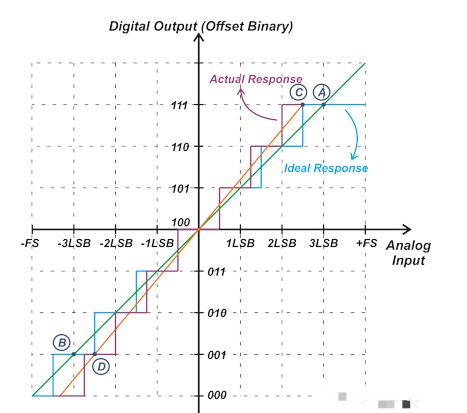
圖 5. 特性曲線示例
在本例中,點 A 和 C 分別比理想響應和實際響應的最后一個轉換高 0.5 LSB。類似地,在理想和實際傳輸曲線上分別選擇接近負滿量程(0.5 LSB 低于 010 到 001 過渡)的點 B 和 D。通過 A 和 B 的線是理想響應,而通過 C 和 D 的線是系統(tǒng)的實際響應。可以將實際斜率與理想斜率進行比較,以確定增益誤差。
在上面的示例中,理想斜率由下式給出:
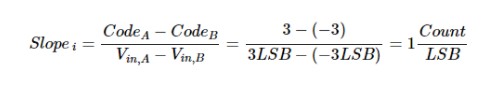
在此等式中,使用了輸出代碼的十進制等效值。另外,請注意代碼的符號。正如預期的那樣,理想的斜率是 1。可以通過類似的方式找到測量的斜率:
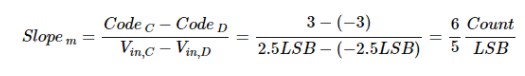
增益誤差可由以下等式定義:
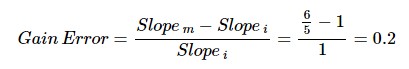
這意味著測得的響應有 20% 的增益誤差。使用高性能 ADC,增益誤差可能小到可以用 ppm 表示。
請記住,在實踐中,我們選擇找到響應斜率的點不一定是傳遞函數(shù)的端點。根據(jù)系統(tǒng)中可用的測試信號和系統(tǒng)線性的輸入范圍,我們可以選擇適當?shù)狞c來確定傳遞函數(shù)的斜率。例如,在確定滿量程值為 3 V 的 ADC 的斜率時,系統(tǒng)中已有的準確 1.5 V 輸入可能被認為足夠接近正滿量程值。
偏移和增益誤差導致未使用的輸入和輸出值
對于單極性和雙極性 ADC,失調誤差會導致未使用的輸入范圍和未使用的輸出代碼。圖 6 顯示了負偏移如何將輸入范圍的下限限制為高于 -FS 的值。對于負偏移,可能也不會使用低于標稱最大代碼的輸出代碼范圍。
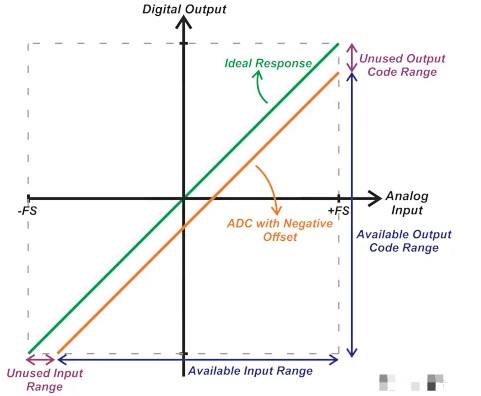
圖 6. 顯示負偏移如何將輸入范圍的下限限制為高于 -FS 的值的圖表。
正如您可能想象的那樣,失調誤差將以類似的方式影響單極 ADC 的范圍。例如,考慮一個單極 12 位 ADC,其滿量程電壓為 2.5 V,偏移為 -8 mV。這對應于大約 -13 LSB 的偏移量。理想的直線響應向下移動了 13 LSB。因此,如圖 7 所示,輸入模擬范圍減少了 13 LSB(或 8 mV),并且不使用最后 13 個輸出代碼。
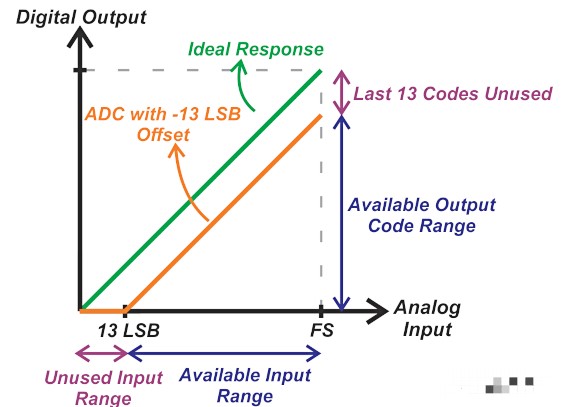
圖 7. 顯示輸入模擬范圍減少 13 LSB 的圖表。
重要的是要記住,更高分辨率 ADC 中的相同偏移電壓會導致更大的未使用代碼范圍。例如,F(xiàn)S = 2.5 V 的 16 位 ADC 中相同的 -8 mV 偏移對應于大約 -210 LSB。在這種情況下,不使用最后的 210 個輸出代碼。圖 8 顯示了正偏移對 ADC 輸入和輸出范圍的影響。
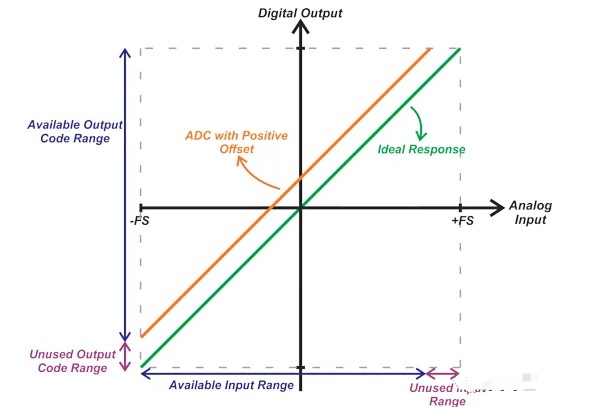
圖 8. 正偏移對 ADC 輸入和輸出范圍的影響。
在這種情況下,不使用來自輸出代碼范圍低端的一些代碼,并且在小于 +FS 的輸入電平處達到最大 ADC 輸出。正增益誤差會限制兩端的輸入范圍,如圖 9 所示。
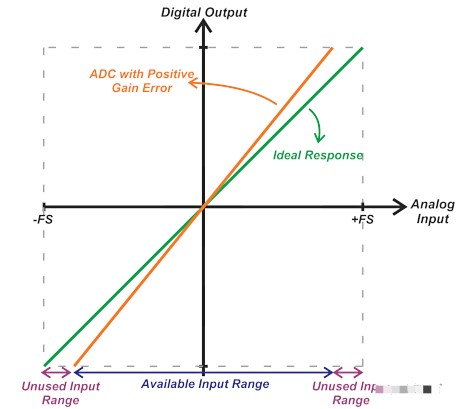
圖 9. 顯示正增益誤差如何限制兩端輸入范圍的圖表。
同樣,負增益誤差可能導致標稱范圍兩端的未使用輸出代碼(圖 10)。
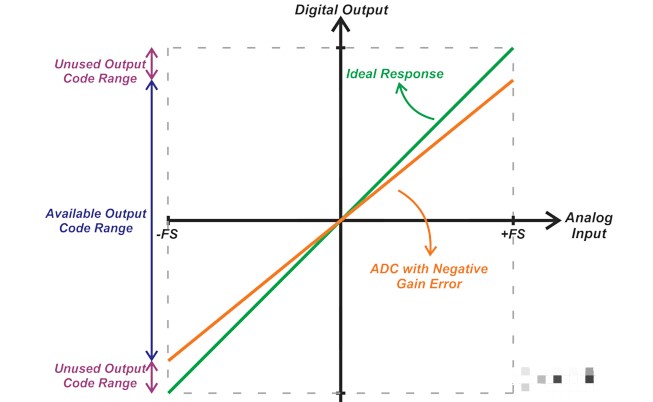
圖 10. 負增益誤差如何導致標稱范圍兩端未使用的輸出代碼。
現(xiàn)在我們已經(jīng)熟悉了 ADC 中的失調和增益誤差概念,我們可以深入討論這兩個誤差項的校準。
ADC 增益和偏移校準
偏移和增益誤差可以在數(shù)字域中輕松校準。為此,應將準確的模擬輸入應用于 ADC 以確定實際響應。在已知實際響應的情況下,可以在數(shù)字域中校正 ADC 輸出代碼以匹配理想響應。
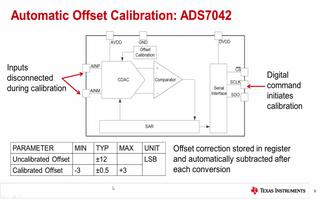
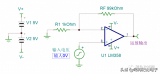
由于給定的 ADC 代碼不對應于單個模擬輸入值,因此只能通過測量代碼轉換來確定實際的 ADC 響應。這需要一個可以產(chǎn)生不同電壓電平的精密電源。圖 11 顯示了可用于確定代碼轉換的測試設置。
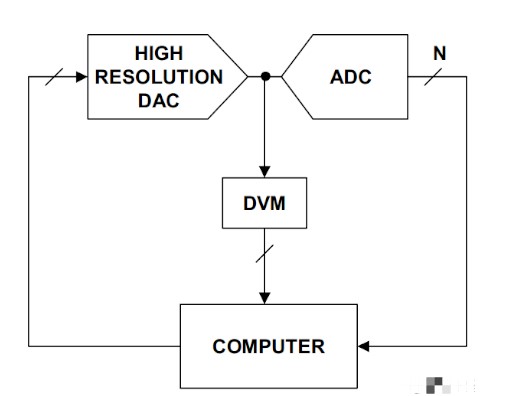
圖 11. 用于確定代碼轉換的示例測試設置 圖片由Analog Devices提供。
在這種情況下,高分辨率數(shù)模轉換器 (DAC)用于在 ADC 輸入端生成不同的電壓電平。DAC 應提供明顯高于被測 ADC 的精度。此外,DAC 輸出端的電壓表可準確測量發(fā)生代碼轉換的電壓電平。處理電壓表和 ADC 的輸出以確定偏移和增益誤差,以及 ADC 的非線性。這種基于 PC 的方法可以使用信號平均等數(shù)字信號處理 (DSP)技術來降低 ADC 噪聲對測量的影響。
在許多應用中,例如傳感器測量系統(tǒng),不可能使用上述設置來測量代碼轉換。在這些情況下,系統(tǒng)中可能只有一個或兩個精確電壓電平可用,從而實現(xiàn)單點或兩點測量。這些測試只能近似實際響應,不能完全消除失調和增益誤差。但是,它們仍然是可以顯著降低偏移和增益誤差的有效方法。
偏移校準——單點校準
單點校準測量傳遞函數(shù)上單點的 ADC 響應,并使用結果來降低偏移誤差。接地電位是用于單點校準的準確、常用的測試輸入,因為它已經(jīng)在系統(tǒng)中可用。作為應用此方法的示例,請考慮圖 3 中所示的響應,為方便起見,下面將其重復,如圖 12 所示。
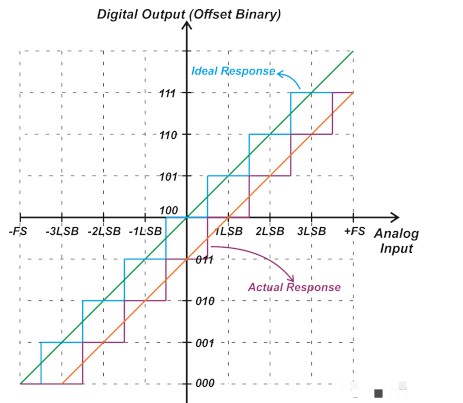
圖 12. 圖 3 的重復顯示了偏移值為 -1 LSB 的三位雙極性 ADC 的傳遞函數(shù)。
如果我們對該 ADC 施加零電壓,則輸出為 011。將其與理想值 100 進行比較,我們可以確定 ADC 的偏移為 -1 LSB。另一個示例如下圖 13 所示。
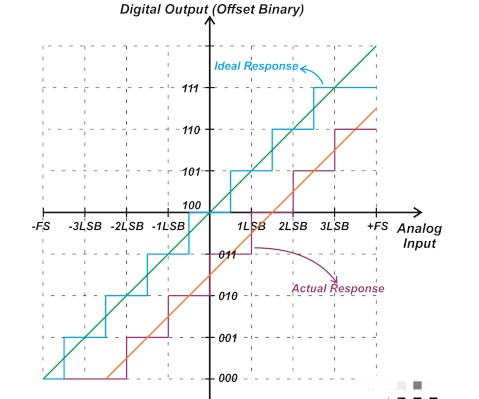
圖 13. 顯示在 ADC 上施加零電壓后 ADC 偏移為 -1 LSB 的示例。
在這種情況下,從 010 到 011 的轉變發(fā)生在零伏以下。再次將輸入短接到地會產(chǎn)生 011。基于此單點測量,ADC 偏移為 -1 LSB。然而,考慮到代碼轉換,我們觀察到實際偏移量為 -1.5 LSB。如您所見,通過單點測量,確定偏移的誤差可能高達 ±0.5 LSB。盡管如此,這種錯誤在大多數(shù)應用中是可以接受的,特別是考慮到這種方法具有最低的成本和復雜性這一事實。單點測量無法確定增益誤差。
一旦確定了偏移,我們可以通過從每個 ADC 讀數(shù)中減去偏移來補償它。通過地電位的單點校準只能用于雙極性或差分輸入 ADC。對于單極性 ADC,負偏移會導致未使用的輸入值位于標稱輸入范圍的下限。下面描述的示例(圖 14)進一步闡明了這個問題。
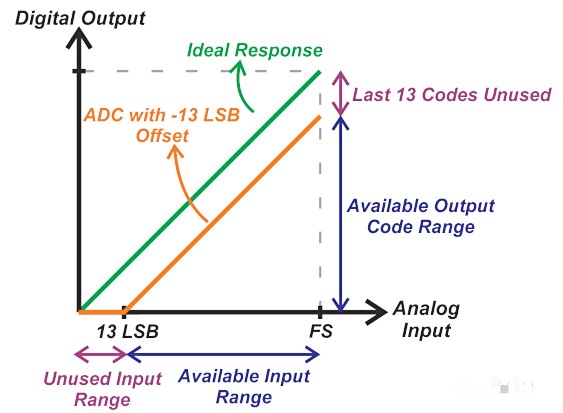
圖 14. 顯示負偏移的示例導致未使用的輸入值處于標稱輸入范圍的下限。
在這種情況下,ADC 的偏移為 -13 LSB。但是,對輸入施加零電壓會產(chǎn)生全零輸出代碼,從而導致零電壓的偏移測量不正確。這就是為什么對于單極性 ADC,我們需要 ADC 可用輸入范圍內的精密電壓來測量和校準偏移誤差。
 電子發(fā)燒友App
電子發(fā)燒友App











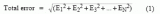











評論