回顧 2015,DFinity 項目提出了令整個社區都為之興奮的隨機信標方案 —— 使用 BLS 門限簽名產生隨機輸出,同時保證輸出的無偏性及不可預測性。然而,時至 2020 年的今天,構建無偏且不可預測的隨機信標仍然困難重重,還在研究的項目少之又少。
其實門限簽名只是構建隨機信標的可行方法之一,我們前面發表過一篇概覽文章,介紹其他可能的解決方法,其中包含本文要重點提到的一種。其他細節 —— 隨機信標是什么?什么是無偏性及不可預測性?除了門限簽名還有什么方法 —— 這些問題都能在上述概覽中得到解答。
經過了多次設計迭代,我們最終提出類似 DFinity 的方案,這也是我們進一步深入理解隨機信標的大好契機。
本文將以淺顯的形式,講述門限簽名生成隨機數的一系列協議。
密碼學基礎知識
為了更好地了解本文中提到的隨機信標,我們需要掌握一些基礎密碼學知識。首先,我們必須區分兩個概念:1. 在本文中以小寫字母(例如 x、y)表示標量,或者說普通常量;2. 用大寫字母表示橢圓曲線上的點(elliptic curve point)。
我們不需要對橢圓曲線點了解得很透徹,只要掌握下面兩點:
1. 橢圓曲線點可以相加,也可以跟標量相乘(本文里用 xG 表示,用 Gx 表示也很常見),然后得到另一個橢圓曲線點。
2. 即使知道 G 和 xG 的值,也不可能計算出 x 的值。
在本文中,我們還將用到 k-1 階多項式 p(x) ;關于 p(x),你不用想太多,只要把它當成一個方程就好,而且:只要你知道在 k 個不同的 x 下 p(x) 的值,你就能推導出所有 x 的 p(x) 值。
以此類推,對于同一個函數 p(x) 和基點 G,如果你知道 p(x)G 代入 k 個不同的 x 值后的值,就可以推導出所有 x 所對應的 p(x)G 值。
只要明白了有關橢圓曲線點的這些屬性,就能深度理解隨機信標的工作原理了。
隨機信標
假設 1:系統中有 n 個參與者,至少需要其中的 k 位才能產生隨機數。就算控制其中的 k-1 人,你也不能預知隨機信標的輸出結果、無法操縱結果。
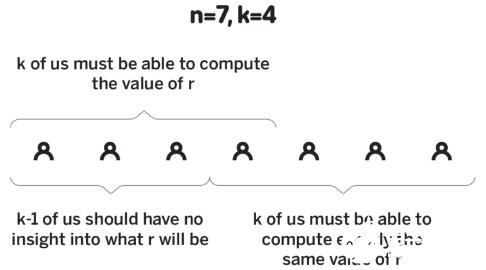
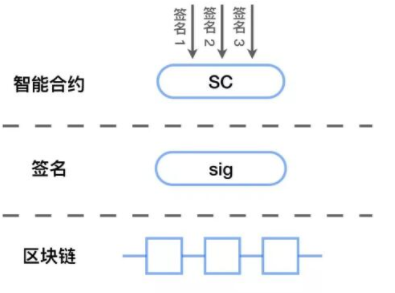
假設 2:現在有個 k-1 階多項式 p(x),參與者 1 知道 p(1) 的值、參與者 2 知道 p(2) 的值、…… 、參與者 n 知道 p(n) 的值;大家約好使用 G 作為橢圓曲線基點,所有參與者都知道 p(x)G 代入所有 x 的值。我們將 p(i) 視為參與者 i 的 “私人份額(不公開,只有參與者自己知道)” ,而 p(i)G 是其 “公開份額”(所有參與者都能知道這個值)(回想一下前文,我們說過無法從 p(i)G 倒推出 p(i),所以只有參與者 i 知道 p(i) 的值)
要設計好的隨機信標,最困難的部分,就是要找到這么一個多項式,使得每個參與者都能知道自己的私人份額,但是無法知道他人的私人份額——這也被稱為分布式密鑰生成(DKG,Distributed Key Generation)。DKG 會放在下個章節討論,現在就先假設存在這么個多項式,而所有人都知道各自的私人份額。
我們接著討論,如何使用這套假設在區塊鏈協議中產生一個隨機信標?假設網絡產生一個區塊,區塊哈希為 h。現在參與者們想用 h 作為種子以生成隨機數,首先用約定好的函數,將 h 轉換為某條橢圓曲線上的一個點:
H = scalarToPoint(h)
對于參與者 i 來說,因為他知道 p(i) 和 H,所以可以自行計算出 H_i = p(i)H。對外公布 H_i 并不會導致參與者 i 的私人份額 p(i) 暴露,因此在每個區塊中都能重用同樣的私人份額,因此 DKG 只需要進行一次。
根據前面提到的第三點特性,當至少有 k 位參與者公布他們各自的 H_i = p(i)H 之后,其他人就能知道代入任何一個 x 之后,H_x = p(x)H 是什么。然后所有參與者都可以在自己本地計算 H_0 = p(0)H,并以這個結果的哈希值作為隨機信標的輸出;請注意,因為沒有參與者知道 p(0),所以唯一能得到 p(0)H 的方法就是對p(x)H 進行內插法(intepolate)計算,要完成內插計算需要知道至少 k 個p(i)H 的值。如果公布的人不足 k 位,則其他人無法推出 p(0)H 的值。
基于此技術構建的信標延續了這些我們所需的特性:如果攻擊者只掌控了少于 k-1 位參與者,則他無法操控隨機信標的輸出;其他 k 位參與者才能計算出最終輸出,他們的子集或其他更多的參與者,都能得出相同的輸出。
我們還忽略了一件事。為了使用插值法計算 p(0)H,必須保證參與者 i 所公開的 H_i 真的等于 p(i)H。但是因為除了參與者 i,其他參與者都不知道 p(i) 是什么,所以沒法直接驗證參與者 i 公布的 H_i 是否的確等于 p(i)H;如果不要求為 H_i 附上密碼學證明,攻擊者可以直接聲稱某個 H_i 的值,而其他人沒有辦法辨別真偽。
有至少兩種密碼學證明辦法,可以用來判別 H_i 的真偽。我們會在聊完 DKG 之后介紹。
分布式密鑰生成(DKG)
根據前面章節對隨機信標的介紹,我們需要 n 位參與者共同使用某個 k-1 階多項式 p(x),使得每個參與者 i 知道自己的 p(i),而其他人無法得知。下一步,需要所有參與者都知道:給定 G 時,所有的 x 所對應的 p(x)g 值。
在本章節,我們假設每個人都有自己的私鑰 x_i,而且其他人都知道 x_i 對應的公鑰 X_i。
那么運行 DKG 的一種方式如下:
1. 每個參與者 i 在本地運行 k-1 階多項式 p_i(x) 的計算。接著用公鑰 X_j 將每個 p_i(j) 加密( j≠i ), 并發送給對應的參與者 j 。如此一來,只有參與者 j 能解密出 p_i(j);參與者 i 還要公布所有 p_i(j)G ,j∈1~k。
2. 所有參與者要對一個至少由 k 個多項式組成的集合達成共識。因為有些參與者可能掉線,所以他們不可能等到 n 個驗證者都作出如此承諾再進行下一步;只要至少 k 個驗證者都作出 “收到至少 k 個這樣的多項式” 的承諾之后,他們就可以使用某種形式的共識算法(如,Tendermint)對他們所收到多項式的子集 Z 達成共識(Z 包含至少 k 個多項式)。
3. 所有參與者共同驗證加密的 p_i(j) 與公開的 p_i(j)G 是否對應,并從 Z 中移除不合格的多項式。
4. 對于集合 Z 中的每個多項式 p_i(x) ,每個參與者 j 自行計算 p_i(j) 的總和作為私人份額 p(j) ;同樣的,對于集合 Z 中的每個 p_i(x)G ,參與者可以計算 p_i(x)G 的總和作為公開份額 p(x)G。
因為 p(x) 是每個獨立的 p_i(x) 的總和,每個 p_i(x) 都是 k-1 階多項式,所以要觀察 p(x) 是否也是 k-1 階多項式。其次要注意,每個參與者 j 只知道 p(j) 的值,但不知道其他 p(x) (x ≠ j )的值。實際上,為了知道 p(x)的值,TA 需要知道所有的 p_i(x),只要至少一個被承諾多項式的值屬于未知,TA 就不可能知道 p(x)。
上述步驟組成了完整的 DKG 過程。步驟 1、2、4 相對直觀,但第 3 步就比較復雜了。
具體來解釋第三步 —— 我們需要找個方法,證明每個加密的 p_i(j) 與公開的 p_i(j)G 存在對應關系。如果沒有這種驗證,攻擊者 i 可以向參與者 j 胡亂發送消息,而不是發送正確的加密 p_i(j),導致參與者 j 無法進一步計算自己的私人份額。
雖然有辦法可以制作出加密份額的形式正確性密碼學證明。但是,這樣的證明數據過大,并且要向全網公布這樣的證明,時間復雜度可能高達 O(nk),證明的 size 是嚴重的瓶頸。
在 NEAR 協議中,我們不去證明 p_i(j) 與公開的 p_i(j)G 的關系,而是在 DKG 過程中給予每個參與者充分的時間(也就是對多項式集合 Z 取得共識、到最終聚合出私有份額,兩個事件之間的時間間隔),去證明“他們收到的 p_i(j) 與公開廣播的 p_i(j)G 對不上”。協議中假設每個參與者在窗口期內(大約半天)至少會上線一次,而他們提交的挑戰就能進入區塊鏈。對于區塊生產者來說,這兩個假設都很合理,因為要做區塊生產者,一般來說在整個 epoch 中都要在線;如果大多數區塊生產者密謀不接收這條消息,其實整個系統就已經不安全,攻擊者其實有更好的方式攻擊整個系統(而不僅僅是拒收挑戰消息)。

假如某個區塊生產者收到無效的公開份額,而且沒有及時在 DKG 過程中提出挑戰,則該礦工也無法在該時段中參與隨機數生成。請注意,只要其他 k 個誠實的參與者都能正確計算出份額(通過不接收任何無效份額,或及時挑戰所有無效份額),協議仍將正常運作。
證明
還剩下最后一個問題:我們如何以不透露 p(i) 為前提,證明自己公布的 H_i 等于 p(i)H?
回想一下,每個參與者都知道 H、G 、p(i)G 的值。在給定 p(i)G 和 G 的情況下回推 p(i) 的運算被稱為離散對數問題,又簡稱為 dlog 。那么每個參與者想做的都是:既能向他人證明 dlog(p(i)G, G) = dlog(H_i, H),又不會透露 p(i)。的確存在這么一種方法構建上述證明,其中之一就是 —— Schnorr 協議;通過 Schnorr 協議,參與者能在發布 H_i 時附上 H_i 的正確性證明。
回想一下,隨機信標連的輸出是 H_0 的內插值(interpolated value)。對于沒有參與生成隨機信標輸出的人來說,除了 H_0,還需要哪些信息來驗證這個值的正確性?因為每個人都能自行在本地計算中加入 G_0,所以只要證明 dlog(G_0, G) = dlog(H_0, H) 就行了。但因為信標的特性,我們無法得知 p(0),也就無法通過 Schnorr 協議生成這樣的證明。所以如果你要向其他人證明 H_0 的正確性,就必須保留所有 H_i 的值及其相應的證明。
不過,好消息是,如果有些計算類似于橢圓曲線點乘法,則只需驗證 H_0 × G = G_0 × H 即可證明 H_0 的計算正確無誤。
如果所選的橢圓曲線支持橢圓曲線配對運算(elliptic curve pairings),則這種證明是可行的。在這種情況下,任何知道 G,H 和 G_0 的人都可以核實 H_0(隨機信標的輸出);而且 H_0 也可視作一個集體的多重簽名,證明區塊 n 的正確性得到至少 k 位參與者的檢查認證。
目前我們還未在 NEAR 中使用橢圓曲線配對運算,但未來我們可能會使用,然后利用上文討論的小技巧取代我們當前使用的單一簽名方法。另一方面,DFinity 使用 BLS 簽名,可以利用配對運算來實現上述簽名。
責任編輯;zl
 電子發燒友App
電子發燒友App


























評論