1 hilbert變換
希爾伯特變換是以著名數學家大衛·希爾伯特(David Hilbert)來命名。在數學與信號處理的領域中,一個實值函數的希爾伯特變換(Hilbert transform)——在此標示為H——是將信號g(t)與1/(πt)做卷積,以得到g‘(t)。因此,希爾伯特變換結果g’(t)可以被解讀為輸入是g(t)的線性時不變系統(linear time invariant system)的輸出,而此系統的脈沖響應為1/(πt)。
希爾伯特變換公式:
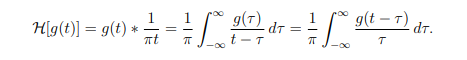
g(t) 的希爾伯特變換是 g(t) 與信號 1/πt 的卷積。 它是脈沖響應為 1/πt 的線性時不變濾波器(稱為希爾伯特變換器)對 g(t) 的響應。 希爾伯特變換 H[g(t)] 通常表示為 ?g(t) 或 [g(t)]∧。
傅立葉變換的相互作用
信號 1/(πt) 進行傅立葉變換:
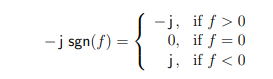
如果 g(t) 有傅里葉變換 G(f),那么,從傅里葉變換的卷積性質,可知 ?g(t) 有傅里葉變換
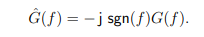
2 希爾伯特變換意義
首先,將實數信號變換成解析信號的結果就是,把一個一維的信號變成了二維復平面上的信號,復數的模和幅角代表了信號的幅度和相位。
這樣看來,似乎復數信號才是完整的,而實信號只是在復平面的實軸上的一個投影。我們知道,解析信號可以計算包絡(瞬時振幅)和瞬時相位。實際上我們計算的包絡就是黑色的線圍成的立體圖形的邊界在實部的投影。
而計算這個邊的投影也很簡單,就是在復平面上的螺旋線中的每一個點的模值,也就是A(t) = sqrt(x^2(t) + Hilbert(x(t))^2),而瞬時相位就是虛部(Hilbert變換后的)和實部(原始信號)在某一時間點的比值的arctan,瞬時頻率就是它的導數。
3 matlab 希爾伯特變換
Hilbert 變換可用于形成解析信號。解析信號在通信領域中很有用,尤其是在帶通信號處理中。工具箱函數 hilbert 計算實數輸入序列 x 的 Hilbert 變換,并返回相同長度的復數結果,即 y = hilbert(x),其中 y 的實部是原始實數數據,虛部是實際 Hilbert 變換。在涉及到連續時間解析信號時,y 有時被稱為解析信號。離散時間解析信號的關鍵屬性是它的 Z 變換在單位圓的下半部分為 0。解析信號的許多應用都與此屬性相關;例如,用解析信號避免帶通采樣操作的混疊效應。解析信號的幅值是原始信號的復包絡。
Hilbert 變換對實際數據作 90 度相移;正弦變為余弦,反之亦然。
close allclear allclc Fs =44100;%44.1khz fc =1000; %1khzN=8192;t=0:(100/Fs):10; x=sin(2*pi*t);y=hilbert(x); figure(1),hold onplot(t,real(y),‘red’);plot(t,imag(y));hold offaxis([0 10 -1.1 1.1])legend(‘Real’,‘imaginary’)
編輯:jq
-
濾波器
+關注
關注
161文章
7860瀏覽量
178926 -
信號處理
+關注
關注
48文章
1042瀏覽量
103401 -
Hilbert
+關注
關注
0文章
9瀏覽量
9004
原文標題:hilbert變換簡介
文章出處:【微信號:leezym0317,微信公眾號:FPGA開源工作室】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
耐能與沙特阿拉伯國家半導體中心達成戰略合作
如何使用傅立葉變換進行頻譜分析
傅立葉變換與拉普拉斯變換的區別
傅立葉變換的基本概念 傅立葉變換在信號處理中的應用
2024羅森伯格全球汽車戰略與銷售會議成功舉辦
經典傅里葉變換與快速傅里葉變換的區別
【AWTK使用經驗】如何在AWTK顯示阿拉伯文本

MATLAB(6)--特殊矩陣
求問MATLAB仿真KK接收器出現的問題?
拉普拉斯變換的作用及意義
開關變換器與諧振變換器的區別
海伯森出席VisionChina上海機器視覺展
【《計算》閱讀體驗】開卷有益,全書與導論
格雷希爾C9對接板總成新能源車測試應用說明—電連接器





 淺析希爾伯特變換簡介以及希爾伯特變換意義
淺析希爾伯特變換簡介以及希爾伯特變換意義










評論