什么是AVL樹
大家好,我是bigsai,好久不見,甚是想念,今天給大家講講AVL樹。
對于樹這種數據結構,想必大家也已經不再陌生,我們簡單回顧一下。
在樹的種類中,通常分成二叉樹和多叉樹,我們熟悉的二叉樹種類有二叉搜索(排序、查找)樹、二叉平衡樹、伸展樹、紅黑樹等等。而熟悉的多叉樹像B樹、字典樹都是經典多叉樹。
普通的二叉樹,我們研究其遍歷方式,因為其沒啥規則約束查找和插入都很隨意所以很少有研究價值。
但是二叉樹結構上很有特點:左孩子和右孩子,兩個不同方向的孩子對應二進制的01,判斷的對錯,比較的大小,所以根據這個結構所有樹左側節點比父節點小,右側節點比父節點大,這時候就誕生了二叉搜索(排序)樹。二叉搜索(排序)樹的一大特點就是查找效率提高了,因為查找一個元素位置或者查看元素是否存在通過每遇到一個節點直接進行比較就可以一步步逼近結果的位置。
但二叉搜索(排序樹)有個很大的問題就是當插入節點很有序,很可能成為一棵斜樹或者深度很高,那么這樣的一個查找效率還是趨近于線性O(n)級別,所以這種情況二叉搜索(排序)樹的效率是比較低的。
所以,人們有個期望:對一棵樹來說插入節點,小的還在左面,大的還在右面方便查找,但是能不能不要出現那么斜的情況?
這不,平衡二叉搜索(AVL)樹就是這么干的,AVL在插入的時候每次都會旋轉自平衡,讓整個樹一直處于平衡狀態,讓整個樹的查詢更加穩定(logN)。我們首先來看一下什么是AVL樹:
-
AVL樹是帶有平衡條件的二叉搜索樹,這個平衡條件必須要容易保持,而且要保證它的深度是O(logN)。
-
AVL的左右子樹的高度差(平衡因子)不大于1,并且它的每個子樹也都是平衡二叉樹。
-
對于平衡二叉樹的最小個數,
n0=0;n1=1;nk=n(k-1)+n(k-2)+1;(求法可以類比斐波那契)
難點:AVL是一顆二叉排序樹,用什么樣的規則或者規律讓它能夠在復雜度不太高的情況下實現動態平衡呢?
不平衡情況
如果從簡單情況模型看,其實四種不平衡情況很簡單,分別是RR,LL,RL,LR四種不平衡情況。
然后將其平衡的結果也很容易(不考慮其附帶節點只看結果),將中間大小數值移動最上方,其他相對位置不變即可:
當然,這個僅僅是針對三個節點情況太過于理想化了,很多時候讓你找不平衡的點,或者我們在解決不平衡的時候,我們需要的就是找到第一個不平衡(從底往上)的點將其平衡即可,下面列舉兩個不平衡的例子:
上述四種不平衡條件情況,可能出現在底部,也可能出現在頭,也可能出現在某個中間節點導致不平衡,而我們只需要研究其首次不平衡點,解決之后整棵樹即繼續平衡,在具體的處理上我們使用遞歸的方式解決問題。
四種不平衡情況處理
針對四種不平衡的情況,這里對每種情況進行詳細的講解。
RR平衡旋轉(左單旋轉)
這里的RR指的是節點模型的樣子,其含義是需要左單旋轉(記憶時候需要注意一下RR不是右旋轉)!
出現這種情況的原因是節點的右側的右側較深這時候不平衡節點需要左旋,再細看過程。
-
在左旋的過程中,
root(oldroot)節點下沉,中間節點(newroot)上浮.而其中中間節點(newroot)的右側依然不變。 -
它上浮左側所以需要指向
根節點(oldroot)(畢竟一棵樹)。但是這樣newroot原來左側節點H空缺。而我們需要仍然讓整個樹完整并且滿足二叉排序樹的規則。 -
而剛好本來oldroot右側指向newroot現在結構改變oldroot右側空缺,剛好這個位置滿足在oldroot的右側,在newroot的左側,所以我們將H插入在這個位置。
-
其中H可能為
NULL,不過不影響操作!
其更詳細流程為:
而左旋的代碼可以表示為:
privatenodegetRRbanlance(nodeoldroot){//右右深,需要左旋
//TODOAuto-generatedmethodstub
nodenewroot=oldroot.right;
oldroot.right=newroot.left;
newroot.left=oldroot;
oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;
newroot.height=Math.max(getHeight(newroot.left),getHeight(newroot.right))+1;//原來的root的高度需要從新計算
returnnewroot;
}
LL平衡旋轉(右單旋轉)
而右旋和左旋相反,但是思路相同,根據上述進行替換即可!
代碼:
privatenodegetLLbanlance(nodeoldroot){//LL小,需要右旋轉
//TODOAuto-generatedmethodstub
nodenewroot=oldroot.left;
oldroot.left=newroot.right;
newroot.right=oldroot;
oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;
newroot.height=Math.max(getHeight(newroot.left),getHeight(newroot.right))+1;//原來的root的高度需要從新金酸
returnnewroot;
}
RL平衡旋轉(先右后左雙旋轉)
這個RL你可能有點懵圈,為啥RR叫左旋,LL叫右旋,這個RL怎么就叫先右后左旋轉了?
別急別急,這個之所以先后后左,是因為具體需要中間節點右旋一次,然后上面節點左旋一次才能平衡,具體可以下面慢慢看。
首先產生這種不平衡的條件原因是:ROOT節點右側左側節點的深度高些,使得與左側的差大于1,這個與我們前面看到的左旋右旋不同因為旋轉一次無法達到平衡!
對于右左結構,中間(R)的最大,兩側(ROOT,R.L)的最小,但是下面(R.L)的比上面(ROOT)大(R.L在ROOT右側)所以如果平衡的話,那么R.L應該在中間,而R應該在右側,原來的ROOT在左側。
這個過程節點的變化浮動比較大,需要妥善處理各個子節點的移動使其滿足二叉排序樹的性質!
這種雙旋轉具體實現其實也不難,不要被外表唬住,這里面雙旋轉我提供兩種解答方法。
思路(標準答案)1:兩次旋轉RR,LL
這個處理起來非常容易,因為前面已經解決RR(左旋),LL(右旋)的問題,所以這里面在上面基礎上可以直接解決,首先對R節點進行一次LL右旋,旋轉一次之后R在最右側,這就轉化成RR不平衡旋轉的問題了,所以這個時候以ROOT開始一次RR左旋即可完成平衡,具體流程可以參考下面這張圖。
思路(個人方法)2:直接分析
根據初始和結果的狀態,然后分析各個節點變化順序=,手動操作這些節點即可。其實不管你怎么操作,只要能滿足最后結構一致就行啦!
首先根據ROOT,R,R.L三個節點變化,R.L肯定要在最頂層,左右分別指向ROOT和R,那么這其中R.left,ROOT.right發生變化(原來分別是R.L和R)暫時為空。而剛好根據左右大小關系可以補上R.L原來的孩子節點A,B。
代碼為:(注釋部分為方案1)
privatenodegetRLbanlance(nodeoldroot){//右左深
//nodenewroot=oldroot.right.left;
//oldroot.right.left=newroot.right;
//newroot.right=oldroot.right;
//oldroot.right=newroot.left;
//newroot.left=oldroot;
//oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;
//newroot.right.height=Math.max(getHeight(newroot.right.left),getHeight(newroot.right.right))+1;
//newroot.height=Math.max(getHeight(oldroot.left),getHeight(newroot.right))+1;//原來的root的高度需要從新金酸
oldroot.right=getLLbanlance(oldroot.right);
oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;
returngetRRbanlance(oldroot);
}
LR平衡旋轉(先左后右雙旋轉)
這個情況和RL情況相似,采取相同操作即可。
根據上述RL修改即可
這部分代碼為
privatenodegetLRbanlance(nodeoldroot){
oldroot.left=getRRbanlance(oldroot.left);
oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;
returngetLLbanlance(oldroot);
}
代碼實現
首先對于節點多個height屬性。用于計算高度(平衡因子)
插入是遞歸插入,遞歸是一個來回的過程,去的過程進行插入,回的過程進行高度更新,和檢查是否平衡。推薦不要寫全局遞歸計算高度,效率太低下,事實上高度變化只和插入和平衡有關,仔細考慮即不會有疏漏!
代碼寫的比較早,如有命名不規范的情況,還請勿噴,如果有疏漏還請指出!
importjava.util.ArrayDeque;
importjava.util.Queue;
publicclassAVLTree{
classnode
{
intvalue;
nodeleft;
noderight;
intheight;
publicnode(){
}
publicnode(intvalue)
{
this.value=value;
this.height=0;
}
publicnode(intvalue,nodeleft,noderight)
{
this.value=value;
this.left=left;this.right=right;
this.height=0;
}
}
noderoot;//根
publicAVLTree(){
this.root=null;
}
publicbooleanisContains(intx)//是否存在
{
nodecurrent=root;
if(root==null){
returnfalse;
}
while(current.value!=x&¤t!=null){
if(xif(x>current.value){
current=current.right;
}
if(current==null){
returnfalse;
}//在里面判斷如果超直接返回
}
//如果在這個位置判斷是否為空會導致current.value不存在報錯
if(current.value==x){
returntrue;
}
returnfalse;
}
publicintgetHeight(nodet)
{
if(t==null){return-1;}//
returnt.height;
//return1+Math.max(getHeight(t.left),getHeight(t.right));這種效率太低
}
publicvoidcengxu(nodet){//層序遍歷
Queueq1=newArrayDeque();
if(t==null)
return;
if(t!=null){
q1.add(t);
}
while(!q1.isEmpty()){
nodet1=q1.poll();
if(t1.left!=null)
q1.add(t1.left);
if(t1.right!=null)
q1.add(t1.right);
System.out.print(t1.value+"");
}
System.out.println();
}
publicvoidzhongxu(nodet)//中序遍歷中序遍歷:左子樹--->根結點--->右子樹
{//為了測試改成中后都行
if(t!=null)
{
zhongxu(t.left);
System.out.print(t.value+"");//訪問完左節點訪問當前節點
zhongxu(t.right);
//System.out.print(t.value+"");//訪問完左節點訪問當前節點
}
}
publicvoidqianxu(nodet)//前序遞歸前序遍歷:根結點--->左子樹--->右子樹
{
if(t!=null){
System.out.print(t.value+"");//當前節點
qianxu(t.left);
qianxu(t.right);}
}
publicvoidinsert(intvalue){
root=insert(value,root);
}
publicnodeinsert(intx,nodet)//插入t是root的引用
{
nodea1=newnode(x);
//if(root==null){root=a1;returnroot;}
if(t==null){returna1;}
//插入操作。遞歸實現
elseif(t!=null)
{
if(xelse
{t.right=insert(x,t.right);}
}
/*
*更新當前節點的高度,因為整個插入只有被插入的一方有影響,
*所以遞歸會更新好最底層的,上層可直接調用
*/
t.height=Math.max(getHeight(t.left),getHeight(t.right))+1;//不要寫成遞歸,遞歸效率低
returnbanlance(t);//因為java對象傳參機制,需要克隆,不可直接t=xx否則變換
}
privatenodebanlance(nodet){
//TODOAuto-generatedmethodstub
//if(t==null)returnnull;
intlefthigh=getHeight(t.left);
intrighthigh=getHeight(t.right);
if(Math.abs(lefthigh-righthigh)<=1)//不需要平衡滴
{returnt;}
elseif(lefthigh//右側大
{
if(getHeight(t.right.left)//RR需要左旋
{
returngetRRbanlance(t);
}
else{
returngetRLbanlance(t);
}
}
else{
if(getHeight(t.left.left)>getHeight(t.left.right))//ll左左
{
returngetLLbanlance(t);
}
else{
returngetLRbanlance(t);
}
}
}
/*
*oldroot(平衡因子為2,不平衡)==>newroot
*//
*Bnewroot(平衡因子為1)oldrootD
*//
*CDBCE
*
*E
*/
privatenodegetRRbanlance(nodeoldroot){//右右深,需要左旋
//TODOAuto-generatedmethodstub
nodenewroot=oldroot.right;
oldroot.right=newroot.left;
newroot.left=oldroot;
oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;
newroot.height=Math.max(getHeight(newroot.left),getHeight(newroot.right))+1;//原來的root的高度需要從新計算
returnnewroot;
}
/*
*右旋同理
*/
privatenodegetLLbanlance(nodeoldroot){//LL小,需要右旋轉
//TODOAuto-generatedmethodstub
nodenewroot=oldroot.left;
oldroot.left=newroot.right;
newroot.right=oldroot;
oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;
newroot.height=Math.max(getHeight(newroot.left),getHeight(newroot.right))+1;//原來的root的高度需要從新金酸
returnnewroot;
}
privatenodegetLRbanlance(nodeoldroot){
oldroot.left=getRRbanlance(oldroot.left);
oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;
returngetLLbanlance(oldroot);
}
/*(不平衡出現在右左節點)
*oldroot==>newroot
*//
*ABoldrootB
*///
*newrootDAEFD
*/
*EF
*/
privatenodegetRLbanlance(nodeoldroot){//右左深
//nodenewroot=oldroot.right.left;
//oldroot.right.left=newroot.right;
//newroot.right=oldroot.right;
//oldroot.right=newroot.left;
//newroot.left=oldroot;
//oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;
//newroot.right.height=Math.max(getHeight(newroot.right.left),getHeight(newroot.right.right))+1;
//newroot.height=Math.max(getHeight(oldroot.left),getHeight(newroot.right))+1;//原來的root的高度需要從新金酸
oldroot.right=getLLbanlance(oldroot.right);
oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;
returngetRRbanlance(oldroot);
}
}
測試情況:
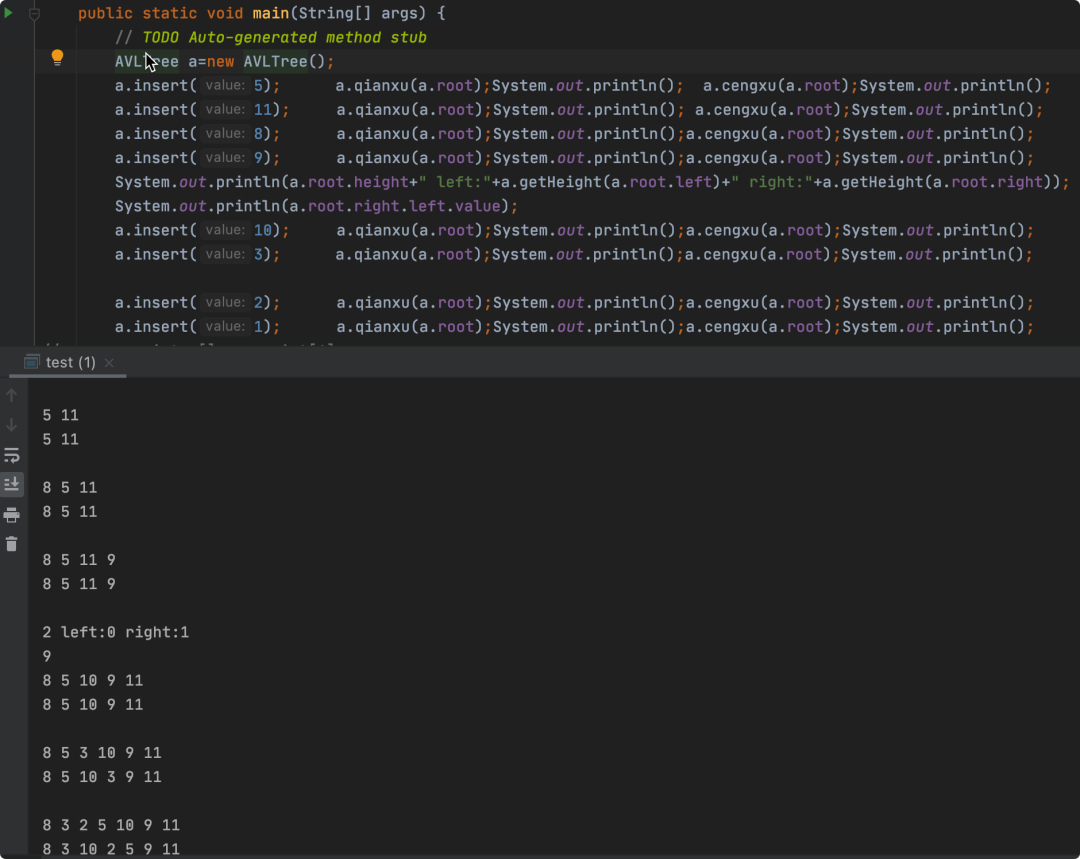
AVL的理解需要時間,當然筆者的AVL自己寫的可能有些疏漏,如果有問題還請各位一起探討!
當然,除了插入,AVL還有刪除等其他操作,(原理相似。刪除后平衡)有興趣可以一起研究。
-
AVL
+關注
關注
0文章
14瀏覽量
10062 -
二叉樹
+關注
關注
0文章
74瀏覽量
12373
原文標題:這個樹,怎么一下就平衡了?
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
平衡電阻器可以改為不平衡嗎
詳解Linux sort命令之掌握排序技巧與實用案例
飛凌嵌入式ElfBoard ELF 1板卡-初識設備樹之設備樹組成和結構
時間復雜度為 O(n^2) 的排序算法

什么是默克爾樹(Merkle Tree)?如何計算默克爾根?
多叉指MOSFET器件靜電防護魯棒性提升技巧
二極管的靜態特性和動態特性詳解
FPGA實現雙調排序算法的探索與實踐

想聽聽48和大對數光纜的排序?
什么是動態線程池?動態線程池的簡單實現思路
C語言實現經典排序算法概覽





 二叉排序樹AVL如何實現動態平衡
二叉排序樹AVL如何實現動態平衡













評論