數據科學家每天都在處理算法。然而，數據科學學科作為一個整體已經發展成為一個不涉及復雜算法實現的角色。盡管如此，從業者仍然可以從對算法的理解和掌握中獲益。

本文介紹、解釋、評估和實現了排序算法merge-sort 。本文的目的是為您提供有關合并排序算法的可靠背景信息，該算法是更復雜算法的基礎知識。

盡管合并排序不被認為是復雜的，但是理解該算法將有助于您認識到選擇最有效的算法來執行與數據相關的任務時需要考慮的因素。創建于 1945 年的 約翰·馮·諾依曼 使用分治方法開發了合并排序算法。

分而治之

要理解合并排序算法，您必須熟悉分治范式，以及遞歸的編程概念。計算機科學領域中的遞歸是指定義用于解決問題的方法在其實現體中調用自身。

換句話說，函數會反復調用自身。

圖 1 。遞歸的視覺圖解——作者的圖像 .

分治算法（合并排序是一種）在其方法中使用遞歸來解決特定問題。分治算法將復雜問題分解為更小的子部分，其中定義的解決方案遞歸地應用于每個子部分。然后分別求解每個子部分，并重新組合解決方案以解決原始問題。

分而治之的算法設計方法結合了三個主要元素：

將較大的問題分解為較小的子問題。（分開）

遞歸使用函數來解決每個較小的子問題。（征服）

最終的解決方案是對較大問題的較小子問題的解決方案的組合。（合并）

其他算法使用分治范式，如快速排序、二進制搜索和 Strassen 算法。

合并排序

在按升序對列表中的元素進行排序的上下文中， merge-sort 方法將列表分成兩半，然后迭代新的兩半，不斷地將它們進一步分成更小的部分。

隨后，對較小的一半進行比較，并將結果組合在一起，形成最終的排序列表。

步驟和實施

合并排序算法的實現分為三步。分而治之，然后結合。

分而治之方法的分而治之部分是第一步。這個初始步驟將整個列表分成兩個較小的部分。然后，列表被進一步分解，直到它們不能再被分割，在每個減半的列表中只留下一個元素項。

合并排序的第二階段中的遞歸循環與按特定順序排序的列表元素有關。在這種情況下，初始數組按升序排序。

在下圖中，您可以看到合并排序算法中涉及的分割、比較和組合步驟。

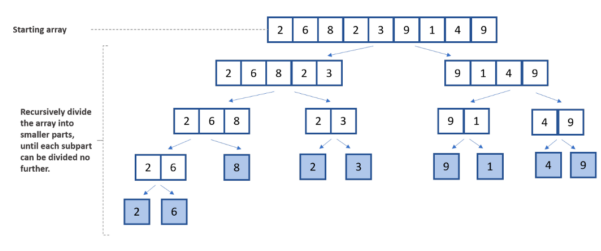
圖 2 。按作者劃分合并排序算法圖像的組件插圖。

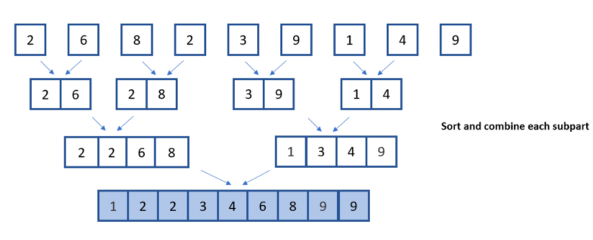
圖 3 。征服和結合的組成部分形象的作者。

要自己實現這一點：

創建一個名為 merge _ sort 的函數，該函數接受整數列表作為參數。以下所有說明均在此功能范圍內。

首先把清單分成兩半。記錄列表的初始長度。

檢查記錄的長度是否等于 1 。如果條件的計算結果為 true ，則返回列表，因為這意味著列表中只有一個元素。因此，不需要劃分清單。

獲取元素數大于 1 的列表的中點。使用 Python 語言時，//執行除法，不帶余數。它將除法結果四舍五入到最接近的整數。這也被稱為樓層劃分。

使用中點作為參考點，將列表拆分為兩半。這是分而治之算法范例的分而治之的一面。

Recursion is leveraged at this step to facilitate the division of lists into halved components. The variables ‘left_half’ and ‘right_half’ are assigned to the invocation of the ‘ merge_sort’ function, accepting the two halves of the initial list as parameters.

“ merge_sort ”函數返回對一個函數的調用，該函數將兩個列表合并，以返回一個組合的排序列表。

• 序列表。

def merge_sort(list: [int]): list_length = len(list) if list_length == 1: return list mid_point = list_length // 2 left_half = merge_sort(list[:mid_point]) right_half = merge_sort(list[mid_point:]) return merge(left_half, right_half)

• 創建一個‘merge’函數，該函數接受兩個整數列表作為其參數。此函數包含分治算法范例的征服和合并方面。以下所有步驟均在此函數體中執行。
• 為保存已排序整數的變量“ output ”分配一個空列表。
• 指針‘i’和‘j’分別用于為左列表和右列表編制索引。
• 在 while 循環中，對左列表和右列表的元素進行比較。每次比較后，輸出列表將填充在兩個比較的元素中。追加元素列表的指針遞增。
• 要添加到排序列表的其余元素是從當前指針值到相應列表末尾的元素。

def merge(left, right): output = [] i = j = 0 while (i < len(left) and j < len(right)): if left[i] < right[j]: output.append(left[i]) i +=1 else: output.append(right[j]) j +=1 output.extend(left[i:]) output.extend(right[j:]) return output unsorted_list = [2, 4, 1, 5, 7, 2, 6, 1, 1, 6, 4, 10, 33, 5, 7, 23]
sorted_list = merge_sort(unsorted_list)
print(unsorted_list)
print(sorted_list)

性能和復雜性

大 O 表示法是一種標準，用于定義和組織算法在空間需求和執行時間方面的性能。

合并排序算法在最佳、最差和平均情況下的時間復雜度相同。對于大小為 n 的列表，合并排序算法要完成的預期步驟數、最小步驟數和最大步驟數都是相同的。

正如本文前面提到的，合并排序算法分為三個步驟：劃分、征服和合并。“分割”步驟涉及到列表中點的計算，無論列表大小如何，它都只需要一個操作步驟。因此，該操作的符號表示為 O（1） 。

“征服”步驟包括劃分和遞歸求解子數組—— logn 表示這一點。“合并”步驟包括將結果合并到最終列表中；此操作執行時間取決于列表大小，并表示為 O（n） 。

平均、最佳和最差時間復雜度的合并排序表示法是 log n * n * O （ 1 ） 。在大 O 表示法中，低階項和常數可以忽略不計，這意味著合并排序算法的最終表示法是 O （ n 日志 n ） 。有關合并排序算法的詳細分析，請參閱 article 。

評價

合并排序在對大型列表進行排序時表現良好，但在較小列表上使用時，其操作時間比其他排序解決方案慢。合并排序的另一個缺點是，即使初始列表已經排序，它也會執行操作步驟。在鏈表排序的用例中，合并排序是最快的排序算法之一。合并排序可用于外部存儲系統（如硬盤）中的文件排序。

關鍵外賣

本文描述了合并排序技術，將其分解為組成操作和逐步過程。

合并排序算法是常用的，與其他排序算法相比，該算法背后的直覺和實現相當簡單。本文包括 Python 中合并排序算法的實現步驟。

您還應該知道，在不同情況下，合并排序方法的執行時間的時間復雜度在最佳、最差和平均情況下保持不變。建議在以下情況下使用合并排序算法：

處理較大的數據集時，請使用合并排序算法。與其他排序算法相比，合并排序在小數組上的性能較差。

鏈表中的元素引用了列表中的下一個元素。這意味著在合并排序算法操作中，指針是可修改的，使得元素的比較和插入具有恒定的時間和空間復雜性。

確定數組是未排序的。即使在排序的數組上， Merge-sort 也會執行其操作，這是對計算資源的浪費。

當考慮到數據的穩定性時，使用合并排序。穩定排序涉及保持數組中相同值的順序。與未排序的數據輸入相比，穩定排序中整個數組中相同值的順序在排序后的輸出中保持在相同的位置。

關于作者

Richmond Alake 是一名機器學習和計算機視覺工程師，他與多家初創公司和公司合作，整合深度學習模型，以解決商業應用中的計算機視覺任務。

審核編輯：郭婷