流體流動計算仿真中存在的一個問題是實驗相關問題。盡管我們在 COMSOL 中可以很容易地生成漂亮的三維可視化數值結果，但將這些結果與實驗結果進行比較通常比較困難。紋影成像是一種實驗技術，它可以生成一組含三維流場的二維圖片。事實上，在 COMSOL Multiphysics? 軟件中也可以很容易地創建這種成像圖。下面，我們來了解更多詳細內容。

紋影成像的背景

紋影成像技術的歷史可以追溯到很遠，甚至可能早于書籍記載。古代穿越沙漠和海洋的旅行者們都非常熟悉海市蜃樓的原理，例如 海市蜃樓和 顛倒的帆船等物體的遙遠幻影（這可能是導致Flying Dutchman這類寓言產生的原因）。發生這些現象是因為光線在穿過不同密度的空氣時會輕微彎曲。這種原理可能在 1000 年前 就以某種形式被人們所理解，但直到最近 500 年左右，人類才開發出這種實驗技術。

雖然紋影成像方法有很多變化，但基本操作原理非常簡單。流體（或固體）內的任何溫度或壓力變化都會導致密度局部變化，而密度會影響折射率。對于大氣，折射率 N和P與密度滿足 Gladstone-Dale 關系：

對于可見光，G約為 0.23 cm3/g。

需要注意的是，上面的表達式只是一個簡單的起點，我們可以使用更完整的表達式，對于氣體混合物和反應流，還有更復雜的表達式。開發紋影成像實驗方法的目的是捕捉到流體中這些密度變化的氣流中光學圖像。

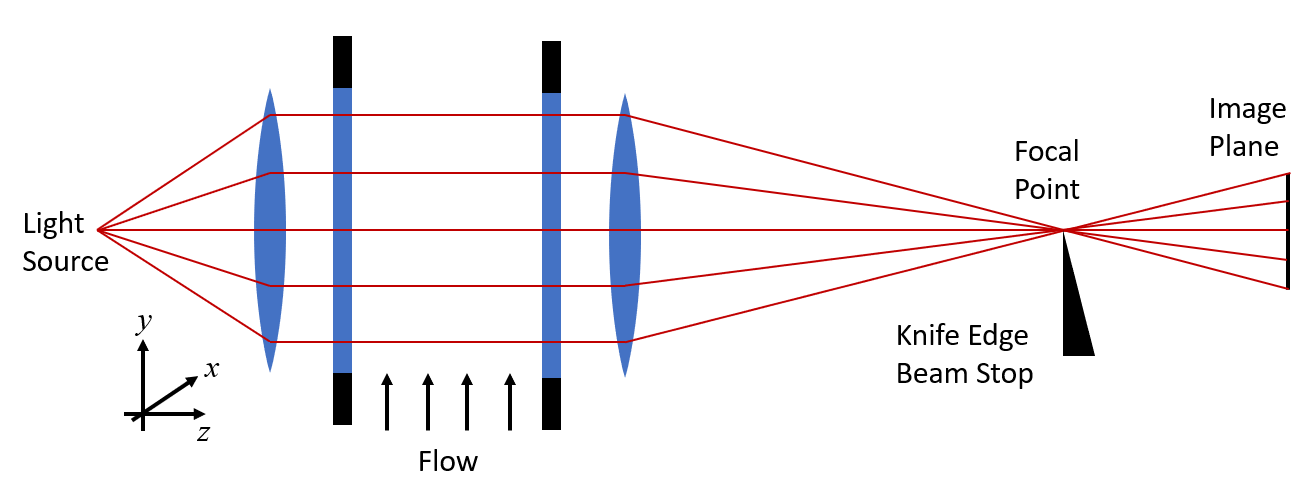
紋影成像設置。

典型的紋影成像實驗裝置如上圖所示。此裝置有兩個透明的窗口，例如圍繞風洞的兩側有一個流場。我們首先假設流場沒有變化。在一側有一個光源，以及一些提供均勻照明的光學元件（透鏡或鏡子）。通過幾何光學方法，我們將這種光視為一組穿過流場的平行光，然后讓它們通過另一組將光線聚焦到圖像平面上的光學元件。

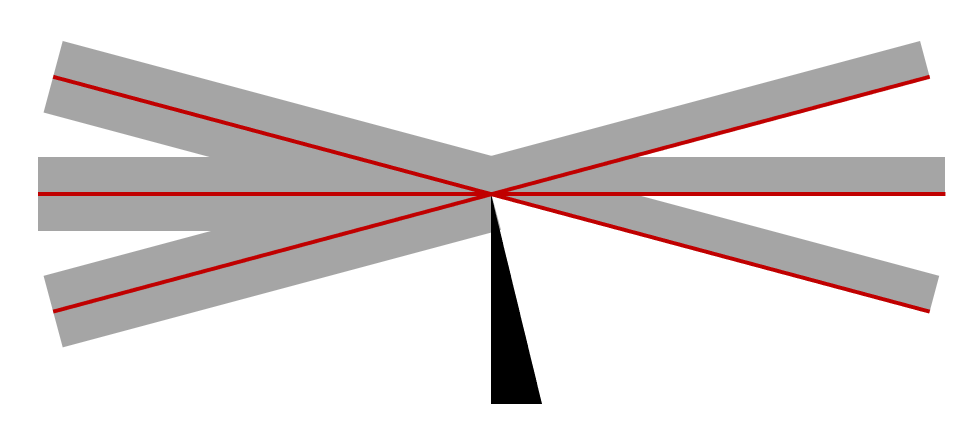
焦點處未受干擾的光線。用刀刃擋住一半的光，并忽略邊緣處的衍射。

但是我們要知道，所謂的焦點不是一個單一的點。光不能被聚焦到一個點上；聚焦光束總會有一些有限的半徑。你可以通過了解電磁波相關知識來理解這個內容。

但是，對于本文而言，我們只需要了解一個關鍵點，就是放置在焦點處的障礙物會遮擋一部分光。這已經足夠保持這個幾何光學方法了。如果我們在焦點處放置一個刀刃（實驗上通常是剃須刀片），就可以阻擋全部光線的一半，但仍然可以獲得完整的圖像，盡管光強只有一半。為了便于理解，我們可以考慮將每條光線看作具有一定的有限厚度，如上圖所示。

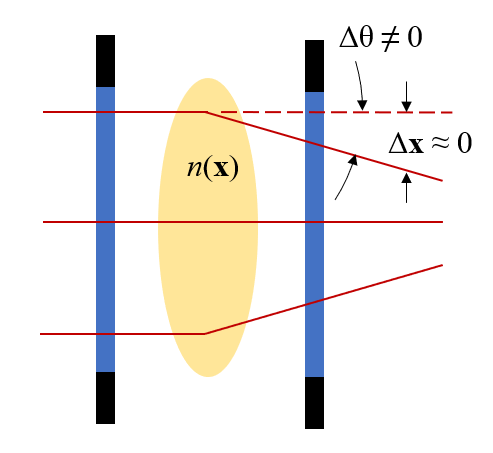
折射率略有變化的區域會稍微改變光線的方向，但不會改變它們在出射平面上的位置。

現在，我們來考慮當流動中存在密度變化時會發生什么。我們已經知道折射率是密度的函數，所以在示意圖中引入一個小的折射率變化，看看會發生什么。上圖顯示了光線的關鍵行為。跳過整個推導，我們僅強調以下幾點：

xy 平面中折射率的變化將導致光束在沿 z 方向傳播時非常輕微地改變方向（角度）

假設當光線通過實驗域時，光線在 xy 平面中的位置變化可以忽略不計

也就是說，在位置 （x，y） 進入域的任何光線都將離開其在xy平面中的原本位置，但會朝著稍微不同的方向前進。接下來，我們看這對焦點有什么影響。正如我們在下圖中看到的那樣，折射率的變化會稍微擾亂光線，因此稍微多一點（或稍微少一點）的光線會被刀刃遮擋。這在圖像平面上顯示為亮區和暗區，并形成基本操作原理。

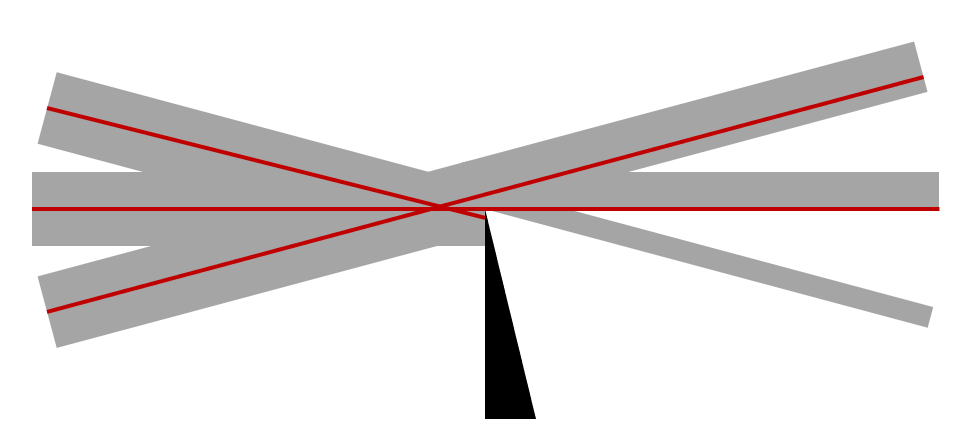
焦點處的擾動光線。對于以略微不同的角度入射的光線，刀刃阻擋的光量不同。

刀刃可以旋轉到平行于 x 軸或 y 軸，或者可以被針孔光束擋板代替，每個擋板都會產生不同的明暗圖案。紋影圖像中的這些亮帶和暗帶對應于流動域中的以下積分：

事實證明，這些積分在 COMSOL Multiphysics 中實現起來非常簡單。

在 COMSOL? 軟件中創建紋影圖像

在創建圖像之前，我們需要先介紹計算流體動力學的一個相關知識：如何處理可壓縮流體 。簡單來說，出于數值建模的原因，我們經常假設流體具有恒定的密度。從流動模型的角度來看，這是完全合理的。小于約 1% 的密度變化可能不會對速度場或壓力場的解產生太大影響，但會顯著改變折射率。因此，如果在假設密度不變的情況下對流動進行建模，例如使用布辛涅斯克近似時，請確保使用壓力場（如果計算了溫度場）對空間密度的變化進行后評估。對于大氣空氣，宜采用理想氣體定律，但請確保這里使用的是絕對壓力而不是表壓。

一旦我們在建模空間中建立了密度變化的表達式，就可以用它來計算折射率分布以及折射率在一個或兩個方向上的導數。為此，我們使用了內置的微分算子。例如，如果密度表達式是變量 rho，我們可以將 x 導數作為 d（rho，x）。我們現在只需要沿流動的方向對該表達式進行積分，并將它們繪制到平行于流動的平面上。為此，我們使用了廣義投影算子，我們甚至可以投影到流動域之外的邊界上，如果我們希望使用比存在于流動域邊界上的網格更精細的網格來評估該算子，這將是非常有利的。

我們還需要考慮當流動中有不透明障礙物時會發生什么。在這種情況下，我們不想用上面的任何一個積分進行求解。我們可以使用從 COMSOL Multiphysics 6.0 版開始提供的CAD 導入模塊、設計模塊，或 LiveLink? 產品中提供的工作平面 投影 功能，將任何障礙物的輪廓投影到光學出射平面邊界上，并且只評估非陰影表面上的積分。

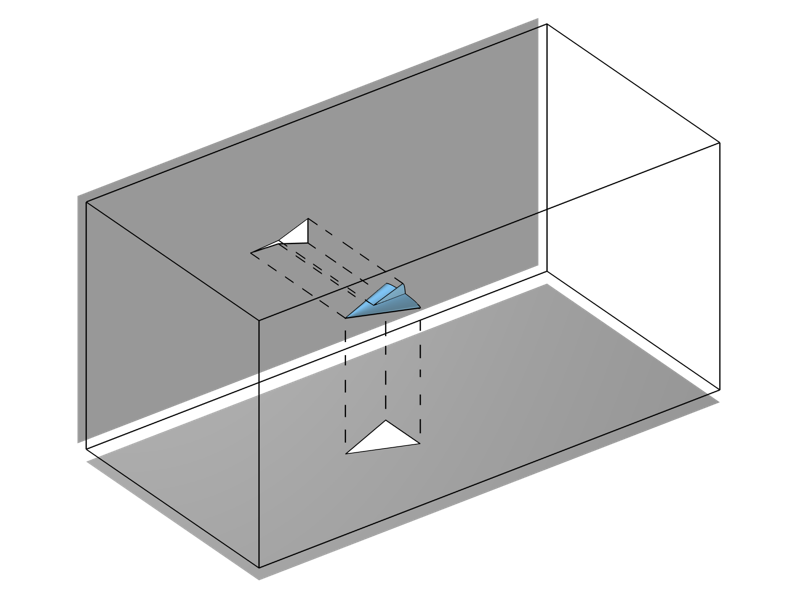
使用 工作平面投影 功能，將幾何圖形的輪廓投影到平面上。

在我們的建模中使用這些技術，可以制作與紋影成像設置的實驗結果相關的圖。下圖是圍繞一個物體的高馬赫數流模擬，這與 含凸起流道中的超音速三維教程模型中演示的類似。同樣的技術也可以用于聲學模型的結果可視化研究中。

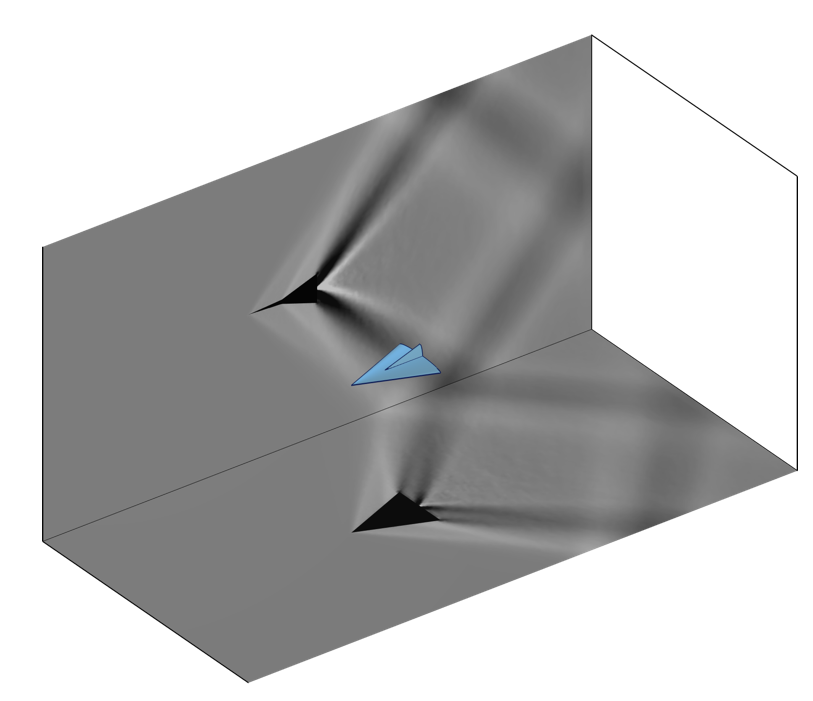
通過 廣義投影 算子創建的與超音速風洞流道模型的紋影成像相關的圖像。