我們周圍的世界越來越數字化,這并不奇怪。一個原因可能是數字形式的數據的操作、存儲和使用比模擬形式更方便、更容易。這使得將模擬信號轉換為數字形式以供進一步處理和使用的電路更加重要。
在任何電路中使用模數轉換器 (ADC) 時,用戶首先詢問的是位數 (NOB),然后是采樣率。但有效位數 (ENOB) 將告訴您有關轉換器本身的大量信息。與 ENOB 一起,采樣頻率、無雜散動態范圍 (SFDR)、積分非線性 (INL) 和微分非線性 (DNL) 是可以指導您選擇預期 ADC 的參數。
在本文中,我將討論各種參數對動態行為的影響,包括對信噪比 (SNR) 影響最大的參數,以及 ADC 的一些靜態行為。我將首先檢查幾個關鍵參數對 SNR 的影響,例如抖動、量化噪聲、輸入信號和 DNL。
抖動
采樣時鐘的不確定性導致采樣電壓的誤差,如圖1所示,描述了時鐘抖動引起的采樣電壓誤差。
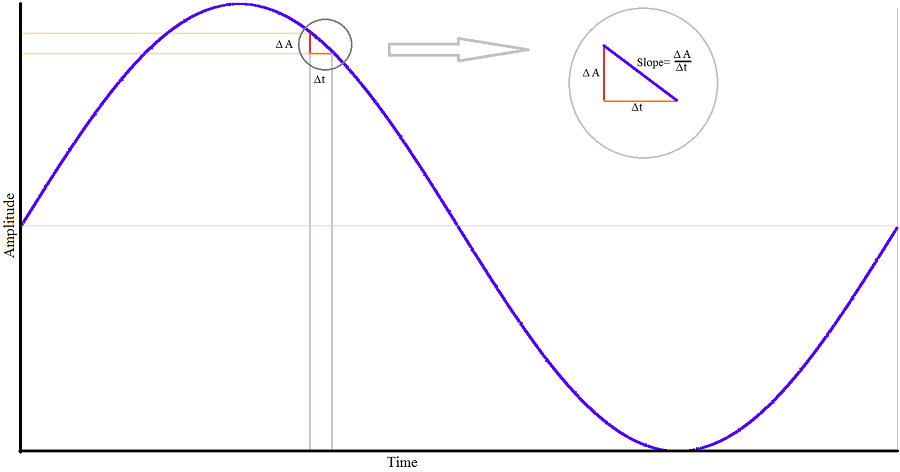
圖 1:采樣時鐘抖動。
考慮V in = V p sin (2p f in )形式的輸入信號。輸入信號對時間的導數是它的變化率。最大變化發生在 cos(2p f in ) 等于 1 時,導致公式 1:
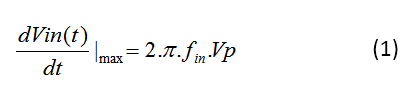
為確保具有滿量程電壓 (VFS) 的給定 N 位 ADC 可容忍來自抖動的電壓誤差 (t j ),它必須小于 V LSB /2 (等式 2),其中V LSB 為由 VFS/2 N定義:
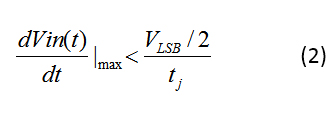
對于公式 1 中的給定正弦波,您可以使用公式 3 求解抖動 (tj):
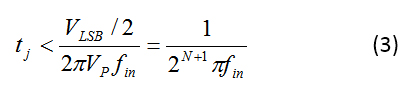
我使用 V p-p = V FS 和V p = 2 N–1 V LSB 來重寫方程。
對于輸入頻率為 80 MHz 的 12 位 ADC,抖動必須小于 485 ps 才不會導致采樣錯誤。
現在讓我們看看抖動對 ADC SNR 的理論影響。如果 V e-RMS是輸入正弦波的 t j的最壞情況均方根 (RMS) 電壓誤差,則公式 4 為:
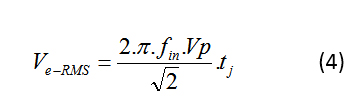
公式 5 將抖動誤差對 SNR 的貢獻表示為:
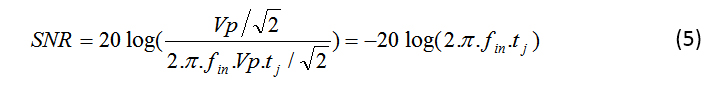
量化噪聲
由于 ADC 代表給定代碼的不同模擬輸入范圍,因此每個數字代碼必然會出現錯誤。簡而言之,盡管為給定代碼分配了一系列模擬輸入,但對于給定代碼,只有一個模擬輸入被準確表示。因此,與給定模擬輸入的分配代碼相關聯的錯誤。該誤差的范圍可以從 –LSB/2 到 +LSB/2。
例如,在圖 2中,2.5 到 3.5 范圍內的所有模擬輸入都用相同的數字代碼表示:0 … 011。
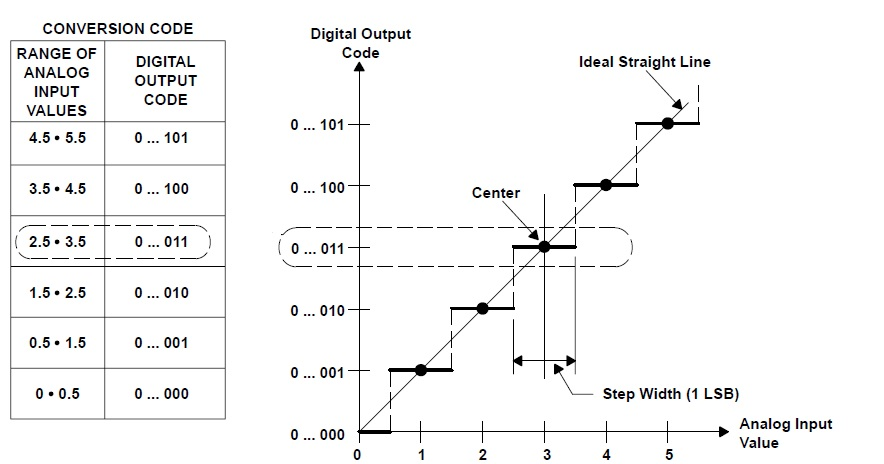
圖 2:ADC 的理想傳遞函數。
此范圍內的每個輸入在范圍邊界處都有較大的誤差(具有不同的極性);當您靠近范圍的中心時,誤差會變小。繪制量化誤差與模擬輸入范圍的關系圖會得到眾所周知的鋸齒圖,如圖3 所示。
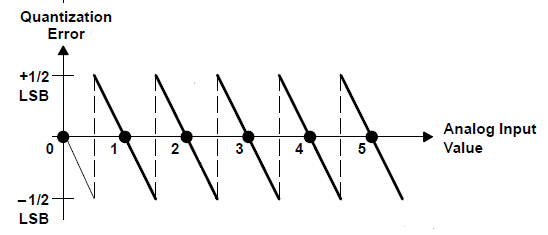
圖 3:固有量化誤差。
等式 6 計算一個步長上誤差的平均噪聲功率(均方),其中q 等于 1 LSB:
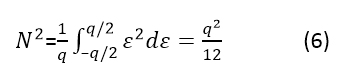
因此,公式 7 給出了 SNR 功率比:
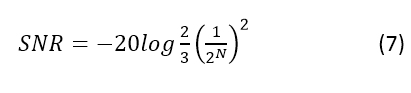
如果將量化噪聲和整體噪聲(復合 RMS DNL)與輸入噪聲一起包含在公式 5 中描述的抖動效應中,您將得到公式 8:
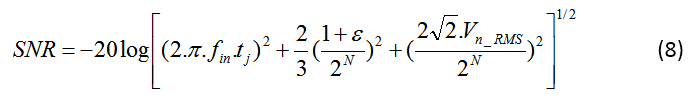
括號內的第一項是前面討論過的抖動的影響。第二項是量化噪聲和線性誤差的影響,第三項是輸入噪聲的影響。
在抖動、量化噪聲和輸入噪聲為零的理想情況下,您將得到以下眾所周知的 SNR 公式(公式 9):
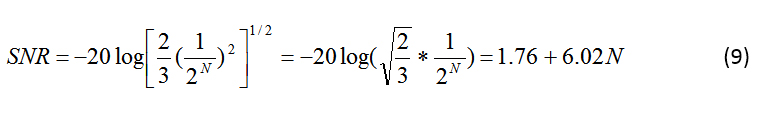
在實踐中,通常使用公式 8 的前兩項,而忽略第三項。您可以使用公式 8 從特定條件下測量的 SNR 計算抖動和量化誤差。為了計算量化誤差,應用了低 f in ,因此抖動的影響可以忽略不計,可以忽略不計。您可以使用得到的低頻 SNR 的測量結果來計算公式 10 中的ε :
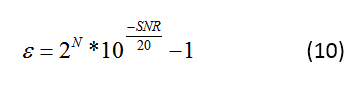
為了計算抖動,應用高頻輸入并再次測量 SNR。在這種情況下,抖動是導致 SNR 下降的主要因素。在f的高頻處使用新的 SNR ,您可以 使用公式 11輕松計算t j :
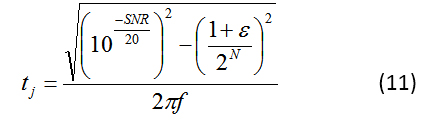
輸入信號
如果輸入不是滿量程,它會相應地降低 SNR,這種影響很容易量化。例如,如果輸入正弦波的幅度為 V in,是滿量程的一小部分,則理想 SNR 將降低 20 log (2V in /V FS )。如果將幅度為 2V 的正弦波應用于 VFS 為 5V 的 12 位 ADC,則輸入將使 74dB 的理論 SNR 降低 1.938dB,從而產生 72.062dB 的 SNR。
ADC 的另一個動態性能參數是信噪比和失真比(SINAD 或 SNRD)。SINAD 與 ENOB 的關聯方式與 SNR 和 NOB 的關聯方式相同。根據定義,您可以通過包括噪聲和總諧波失真 (THD) 效應來計算 SINAD(公式 12):
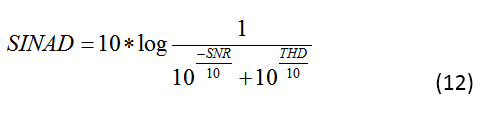
或者,您可以簡單地使用等式 10 并將 SNR 替換為 SINAD,將 N 替換為 ENOB,從而以 ENOB 表示 SINAD。
過采樣
到目前為止,我假設以奈奎斯特速率進行采樣,這意味著采樣率是被采樣信號最大頻率的兩倍。現在,讓我們研究過采樣(超過奈奎斯特速率的采樣)對 SNR 的影響。為此,采樣頻率 (fos) 與奈奎斯特頻率之比 2 fo 就是過采樣率 (OSR = f os /2f 0 )。
但首先,讓我們看一下量化誤差 ε,它在前面的方程中用于計算 SNR。ε具有位于±(Δ/2)之間的相等概率,其中D是LSB或簡單地V FS /2 N。等式 13 將量化噪聲功率表示為:
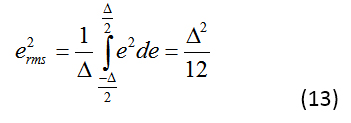
公式 14 給出了落入信號帶寬(0 到 fo)的噪聲功率:
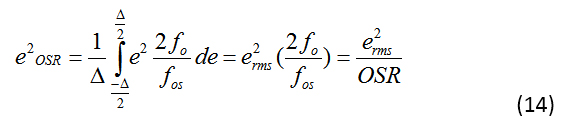
等式 14 說明了一個有趣的點:過采樣降低了感興趣頻帶中的量化噪聲,從而提高了 SNR。事實上,您可以使用公式 15 量化 SNR 的改進:
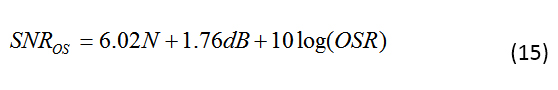
從公式 15 可以看出,SNR 每倍頻程提高 3 dB。因此,如果 OSR = 2,則 SNR 提高 3 dB;如果 OSR = 4,則 SNR 提高 6 dB。
在圖4中,采樣頻率每倍頻程增加了3dB;因此,本底噪聲下降了 9 dB,這相當于提高了相同數量的 SNR。
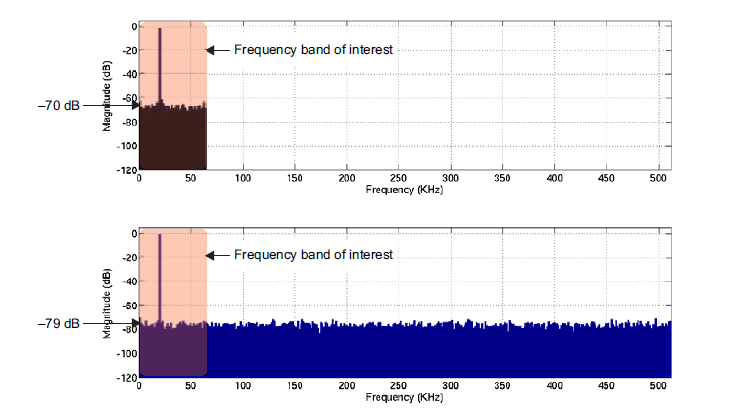
圖 4:由于過采樣而降低了本底噪聲。
DNL
DNL 錯誤會降低整體 SNR。在某個頻率以下,THD 僅取決于 ADC 的整體 INL;超出該頻率,轉換器的動態性能就會出現。
讓我們制定1 LSB DNL的限制,這是不丟失代碼的條件;這相當于分辨率降低 1 位,因此 SNR 降低 6 dB。對于線性誤差為 1 LSB 的 n 位轉換器,公式 16 將線性誤差引起的 SNR 邊界表示為:
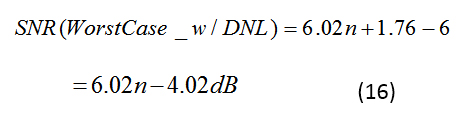
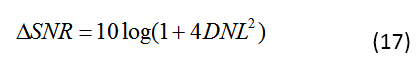
審核編輯:湯梓紅
-
adc
+關注
關注
99文章
6533瀏覽量
545752 -
模數轉換器
+關注
關注
26文章
3218瀏覽量
127018 -
SNR
+關注
關注
3文章
196瀏覽量
24521 -
SFDR
+關注
關注
0文章
38瀏覽量
12953
發布評論請先 登錄
相關推薦
什么是無雜散動態范圍 (SFDR)?為什么 SFDR 很重要?
想要驗證ADC,DAC的SNR和DR指標,可否推薦實際相應的測試方法?
ADS8167 SAR ADC實際測量SNR指標偏小,為什么?
采用滑膜估算的角度和實際的角度總是有相位差,但是觀察由滑膜估算的電流和實際的電流波形基本重合
DDC濾波器是否影響SNR和SFDR?
RFID在實際應用中哪些因素需要我們來考慮
PCB設計的成本考慮因素是什么?
在高速ADC中增加SFDR的局限性分析
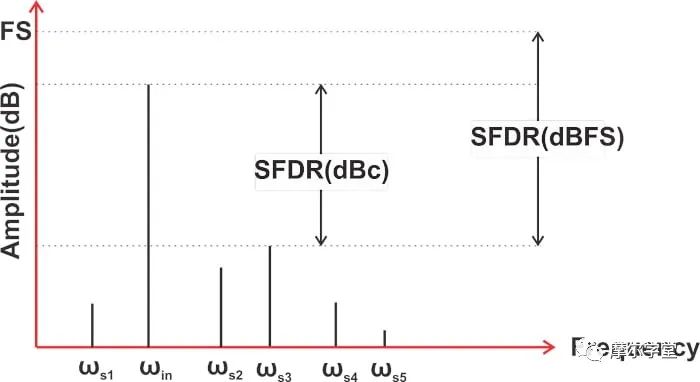
什么是無雜散動態范圍 (SFDR)?為什么SFDR很重要?
了解SINAD、ENOB、SNR、THD、THD + N、SFDR





 估算SNR和SFDR的實際考慮因素
估算SNR和SFDR的實際考慮因素










評論