直線擬合原理

給出多個點，然后根據(jù)這些點擬合出一條直線，這個最常見的算法是多約束方程的最小二乘擬合，如下圖所示:

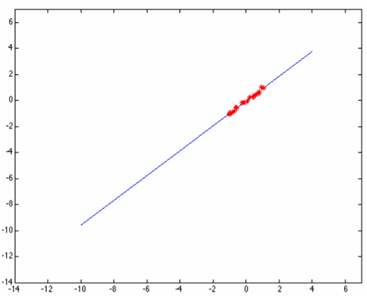
但是當(dāng)這些點當(dāng)中有一個或者幾個離群點(outlier)時候，最小二乘擬合出來的直線就直接翻車成這樣了：

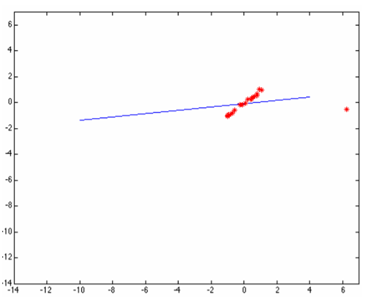
原因是最小二乘無法在估算擬合的時候剔除或者降低離群點的影響，于是一個聰明的家伙出現(xiàn)了，提出了基于權(quán)重的最小二乘擬合估算方法，這樣就避免了翻車。根據(jù)高斯分布，離群點權(quán)重應(yīng)該盡可能的小，這樣就可以降低它的影響，OpenCV中的直線擬合就是就權(quán)重最小二乘完成的，在生成權(quán)重時候OpenCV支持幾種不同的距離計算方法，分別如下：

其中DIST_L2是最原始的最小二乘，最容易翻車的一種擬合方式，雖然速度快點。然后用基于權(quán)重的最小二乘估算擬合結(jié)果如下：

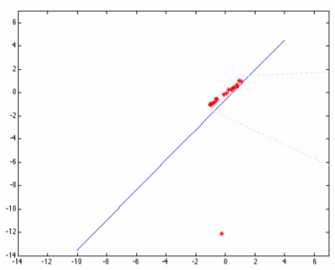
函數(shù)與實現(xiàn)源碼分析

OpenCV中直線擬合函數(shù)支持上述六種距離計算方式，函數(shù)與參數(shù)解釋如下：

points是輸入點集合

line是輸出的擬合參數(shù)，支持2D與3D

distType是選擇距離計算方式

param 是某些距離計算時生成權(quán)重需要的參數(shù)

reps 是前后兩次原點到直線的距離差值，可以看成擬合精度高低

aeps是前后兩次角度差值，表示的是擬合精度

六種權(quán)重的計算更新實現(xiàn)如下：

staticvoidweightL1(float*d,intcount,float*w)
{
inti;


for(i=0;i

	

	擬合計算的代碼實現(xiàn)：

	
staticvoidfitLine2D_wods(constPoint2f*points,intcount,float*weights,float*line)
{
CV_Assert(count>0);
doublex=0,y=0,x2=0,y2=0,xy=0,w=0;
doubledx2,dy2,dxy;
inti;
floatt;

//Calculatingtheaverageofxandy...
if(weights==0)
{
for(i=0;i

	

	案例：直線擬合

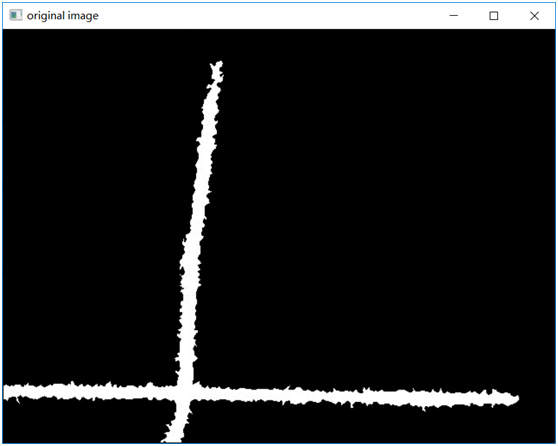
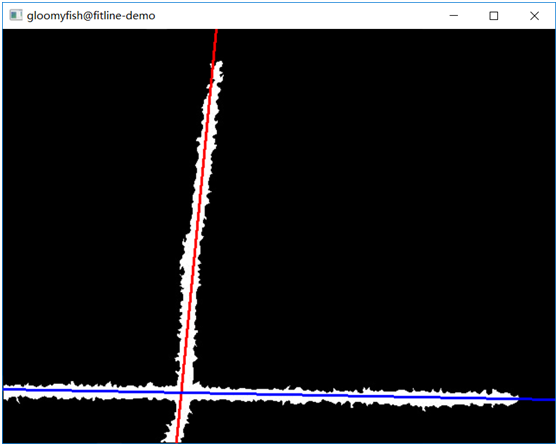
	有如下的原圖：

	

	通過OpenCV的距離變換，骨架提取，然后再直線擬合，使用DIST_L1得到的結(jié)果如下：

	

	



	審核編輯：劉清