算法在編寫成可執(zhí)行程序的時(shí)候,main函數(shù)使用這個(gè)算法,需要調(diào)用一定的空間,消耗一定的時(shí)間。算法的效率就是通過空間和時(shí)間這兩個(gè)維度來評(píng)判的。
時(shí)間復(fù)雜度:衡量一個(gè)算法的運(yùn)行速度
空間復(fù)雜度:衡量一個(gè)算法運(yùn)行需要開辟的額外空間
那么我們今天先來看看時(shí)間復(fù)雜度!
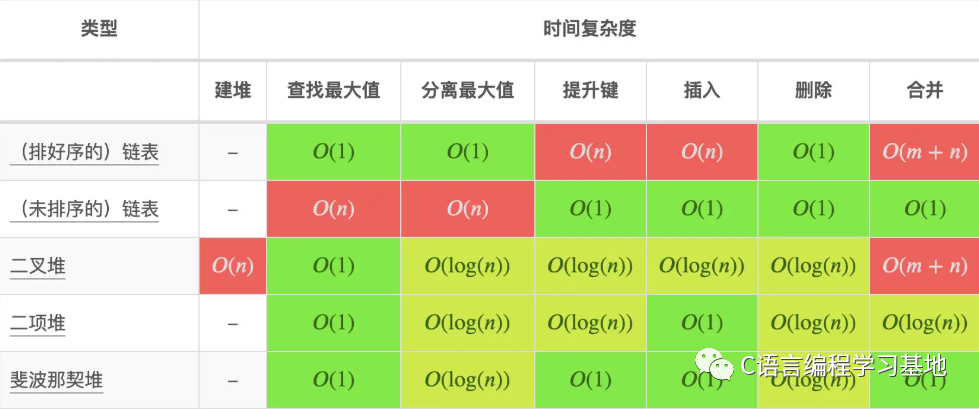
時(shí)間復(fù)雜度
算法的時(shí)間復(fù)雜度是一個(gè)函數(shù),它定量描述了該算法的運(yùn)行時(shí)間。算法中基本操作的執(zhí)行次數(shù),為算法的時(shí)間復(fù)雜度
時(shí)間復(fù)雜度是一個(gè)近似值,并不是實(shí)際運(yùn)行的時(shí)間
實(shí)際上代碼的運(yùn)行時(shí)間,和機(jī)器的內(nèi)存、cpu性能和平臺(tái)都有關(guān)系,同一個(gè)代碼在不同的機(jī)器上運(yùn)行時(shí)間都不一樣,如果只以純粹的時(shí)間來考核,很難分析
找到某條基本語句與問題規(guī)模N之間的數(shù)學(xué)表達(dá)式,就算出了該算法的時(shí)間復(fù)雜度
void Test(int N){int count =0;for(int i=0;i{for(int j=0;j{count++;}}for (int k = 0; k < 2 * N ; ++ k){count++;}int M = 10;while (M--){count++;}return;}
請(qǐng)問這個(gè)代碼中,count語句執(zhí)行了幾次?
F ( N ) = N 2 + 2 ? N + 10 F(N)=N^2+2*N+10 F(N)=N2+2?N+10
N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010
你可能會(huì)簡(jiǎn)單地認(rèn)為,F(xiàn)(N)的結(jié)果就是我們的時(shí)間復(fù)雜度。其實(shí)并不然,我們并不需要一個(gè)精確的運(yùn)行次數(shù),只需要知道程序運(yùn)行次數(shù)的量級(jí)就行了
這里我們使用大O漸進(jìn)表示法來表示時(shí)間復(fù)雜度(空間復(fù)雜度同理)
2.1大O的漸進(jìn)表示法
大O符號(hào)(Big O notation):是用于描述函數(shù)漸進(jìn)行為的數(shù)學(xué)符號(hào)
推導(dǎo)大O階方法:
(1)用常數(shù)1取代運(yùn)行時(shí)間中的所有加法常數(shù)。
(2)在修改后的運(yùn)行次數(shù)函數(shù)中,只保留最高階項(xiàng)。
(3)如果最高階項(xiàng)存在且不是1,則去除與這個(gè)項(xiàng)目相乘的常數(shù)。得到的結(jié)果就是大O階
使用這種方法后,test1函數(shù)的時(shí)間復(fù)雜度為
O ( N 2 ) O(N^2) O(N2)
對(duì)于test1函數(shù),在計(jì)算的時(shí)候,我們省略了最后的+10,保留了最高階數(shù)N2,即得出了它的時(shí)間復(fù)雜度
如果最高階數(shù)前面有系數(shù),如2N,系數(shù)也將被省略
因?yàn)楫?dāng)N的數(shù)值很大的時(shí)候,后面的那些值對(duì)我們總運(yùn)行次數(shù)的影響已經(jīng)非常小了。大O的漸進(jìn)表示法去掉了那些對(duì)結(jié)果影響不大的項(xiàng),簡(jiǎn)潔明了的表示出了執(zhí)行次數(shù)
2.2多種情況取最壞
一些算法的時(shí)間復(fù)雜度會(huì)有最好、最壞和平均的情況
最好情況:任意輸入規(guī)模的最小運(yùn)行次數(shù)(下界)
平均情況:期望的運(yùn)行次數(shù)
最壞情況:任意輸入規(guī)模的最大運(yùn)行次數(shù)(上界)
舉個(gè)例子,當(dāng)我們編寫一個(gè)在數(shù)組中查找數(shù)值的算法時(shí),它可能會(huì)出現(xiàn)這幾種情況:
最好情況:1次就找到
平均情況:N/2次
最壞情況:N次
在實(shí)際中的一般情況,我們關(guān)注的是算法的最壞運(yùn)行情況,所以數(shù)組中搜索數(shù)據(jù)時(shí)間復(fù)雜度為O(N)
2.3常見時(shí)間復(fù)雜度的計(jì)算
NO.1
void Func1(int N){int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d ", count);}
這里出現(xiàn)了兩個(gè)循環(huán),分別是2N次和10次。前面提到了大O漸進(jìn)法只保留最高階數(shù)并省略系數(shù),所以它的時(shí)間復(fù)雜度是O(N)
NO.2
void Func2(int N, int M){int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d ", count);}
這里出現(xiàn)了次數(shù)為N和M的兩層循環(huán):
當(dāng)M和N差不多大的時(shí)候,時(shí)間復(fù)雜度可以理解為O(M)或O(N)
當(dāng)M遠(yuǎn)遠(yuǎn)大于N時(shí),時(shí)間復(fù)雜度為O(M)
一般情況取O(M+N)
NO.3 常數(shù)階
void Func3(int N){int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d ", count);}
這里我們得知了具體的循環(huán)次數(shù)為100,是一常數(shù),時(shí)間復(fù)雜度為O(1),代表常數(shù)階
只要循環(huán)次數(shù)已知,為一常數(shù)且和所傳參數(shù)無關(guān),其時(shí)間復(fù)雜度即為O(1)
NO.4 strchr
//計(jì)算strchr的時(shí)間復(fù)雜度const char * strchr ( const char * str, int character );
看到這道題的時(shí)候,你可能會(huì)一愣,strchr是什么?
可這里面沒有strchr,但有strstr
strstr函數(shù)的作用:在字符串1中尋找是否有字符串2
其中第二個(gè)str代表的是string字符串,那我們是不是可以猜想,chr代表的是char字符,其作用是在一個(gè)字符串中查找是否有一個(gè)字符呢?
當(dāng)然,光是猜想肯定是不夠的,我們還需要求證一下
打開cplusplus網(wǎng)站,搜索strchr,即可轉(zhuǎn)到函數(shù)定義
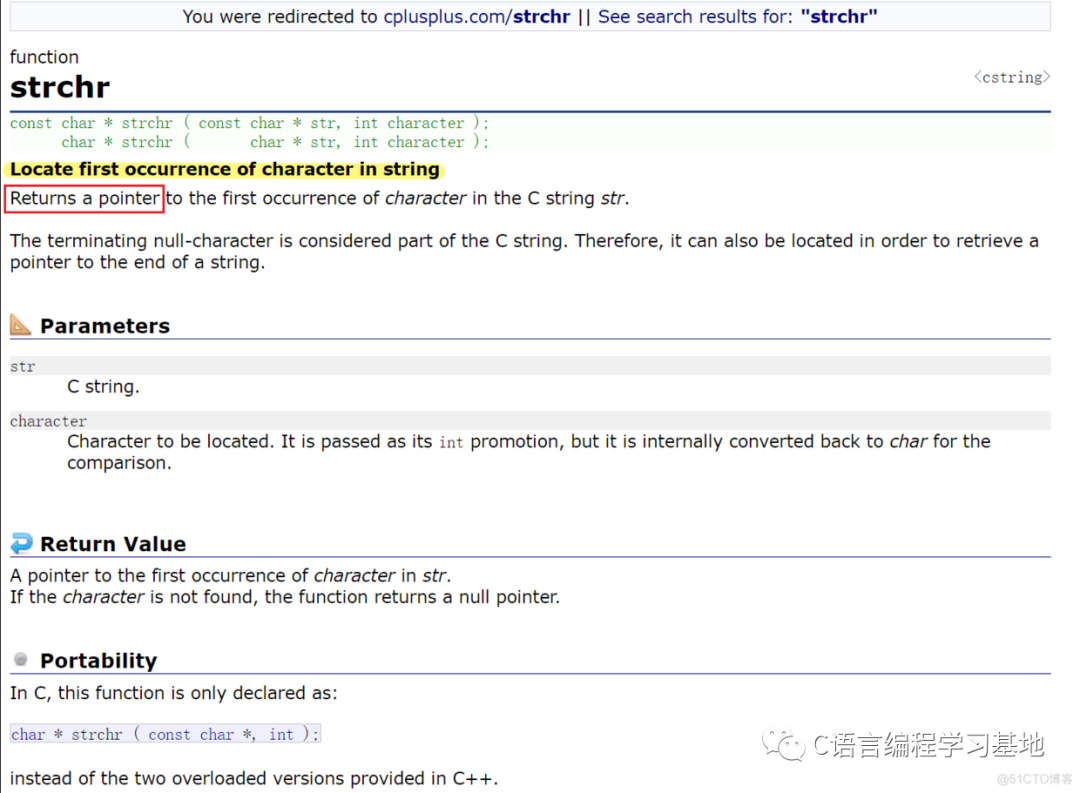
可以看到,該函數(shù)的作用是定位字符串中第一次出現(xiàn)該字符的位置,返回值是一個(gè)pointer指針
和我們猜想的一樣,它的作用就是在字符串中查找一個(gè)字符,并返回它第一次出現(xiàn)的位置的地址。
這樣一來,strchr函數(shù)的時(shí)間復(fù)雜度就很清楚了,就是遍歷字符串所需要的次數(shù),O(N)
NO.5 冒泡排序
voidBubbleSort(int*a,intn){assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}}
冒泡排序是一個(gè)非常經(jīng)典的代碼,其思路就是遍歷整個(gè)數(shù)組,如果待排序數(shù)字大于它的下一位,則交換這兩個(gè)數(shù)字
N個(gè)數(shù)字的數(shù)組需要N-1次排序才能完成
每一次排序都需要遍歷一次數(shù)組
這樣算來,冒泡排序的循環(huán)次數(shù)就是兩個(gè)N,即為O(N2)
能否通過循環(huán)層級(jí)判斷?
細(xì)心的你可能會(huì)發(fā)現(xiàn),上述代碼中出現(xiàn)了兩層循環(huán),那是不是可以通過循環(huán)層級(jí)來判斷時(shí)間復(fù)雜度呢?
并不能!
for(int i=0;i{for(int j=0;j<3;j++)printf("hehe ");}
如果是上述這種兩次循環(huán)的情況,會(huì)打印3n次呵呵,其時(shí)間復(fù)雜度是O(N)而不是N2
我們要準(zhǔn)確分析算法的思路,并不能簡(jiǎn)單地通過循環(huán)層級(jí)來判斷時(shí)間復(fù)雜度
NO.6 二分查找
intBinarySearch(int*a,intn,intx){assert(a);intbegin=0;intend=n-1;while(beginend){intmid=begin+((end-begin)>>1);//使用位移操作符來模擬/2,防止begin和end相加后超出int范圍if(a[mid]begin=mid+1;elseif(a[mid]>x)end=mid;elsereturnmid;}return-1;}
二分查找的思路這里不再贅述
假設(shè)我們找了x次,每一次查找都會(huì)使查找范圍減半
N/2/2/2/2 ……
最后我們可以得出2條公式
2 x = N 2^x=N 2x=N
x = l o g 2 N x=log_2N x=log2N
最好情況:O(1)
最壞情況:O(logN)

通過時(shí)間復(fù)雜度的對(duì)比,我們就能看出二分查找的優(yōu)勢(shì)在那里了

可以看到,當(dāng)數(shù)據(jù)很大的時(shí)候,O(logN)的算法執(zhí)行次數(shù)比O(N)少了特別多!!(來自BT-7274的肯定)
NO.7 計(jì)算N!
// 計(jì)算階乘遞歸Fac的時(shí)間復(fù)雜度?long long Fac(size_t N){if(0 == N)return 1;return Fac(N-1)*N;}
對(duì)于這個(gè)階乘的遞歸函數(shù)而言,每次函數(shù)調(diào)用是O(1),時(shí)間復(fù)雜度主要看遞歸次數(shù)
對(duì)于數(shù)字N而言,遞歸需要N次,時(shí)間復(fù)雜度是O(N)
遞歸算法時(shí)間復(fù)雜度計(jì)算
如果每次函數(shù)調(diào)用是O(1),看遞歸次數(shù)
每次函數(shù)調(diào)用不是O(1),那么就看他遞歸調(diào)用中次數(shù)的累加
NO.8 斐波那契數(shù)列
// 計(jì)算斐波那契遞歸Fib的時(shí)間復(fù)雜度?long long Fib(size_t N){if(N < 3)return 1;return Fib(N-1) + Fib(N-2);}
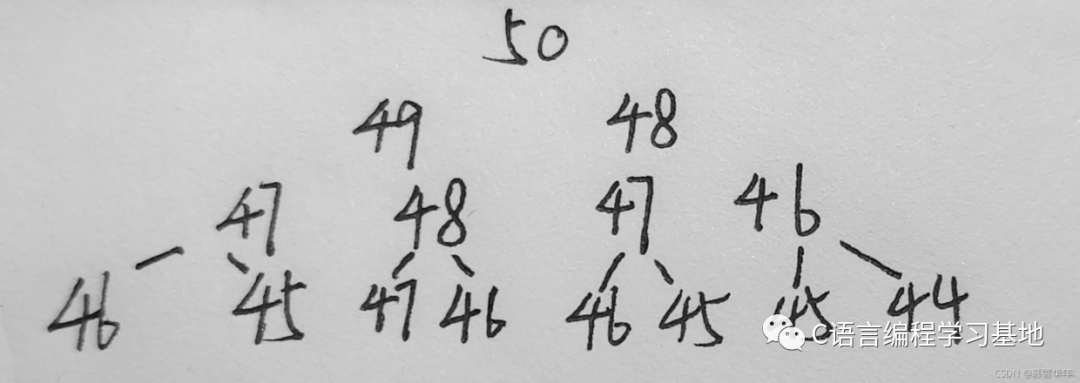
每次遞歸,次數(shù)都會(huì)增加,總的來說是以2^x的量級(jí)增加的(x代表行數(shù))
1 + 2 + 4 + 8 + … … + 2 X ? 2 1+2+4+8+……+2^{X-2} 1+2+4+8+……+2X?2
這里一共有x-1項(xiàng),用等比數(shù)列的求和公式得出,結(jié)果為2x-1
所以最后得出的時(shí)間復(fù)雜度為O(2N)
需要注意的是,當(dāng)遞歸調(diào)用到底部時(shí),有一些調(diào)用會(huì)較早退出,這部分位于金字塔的右下角
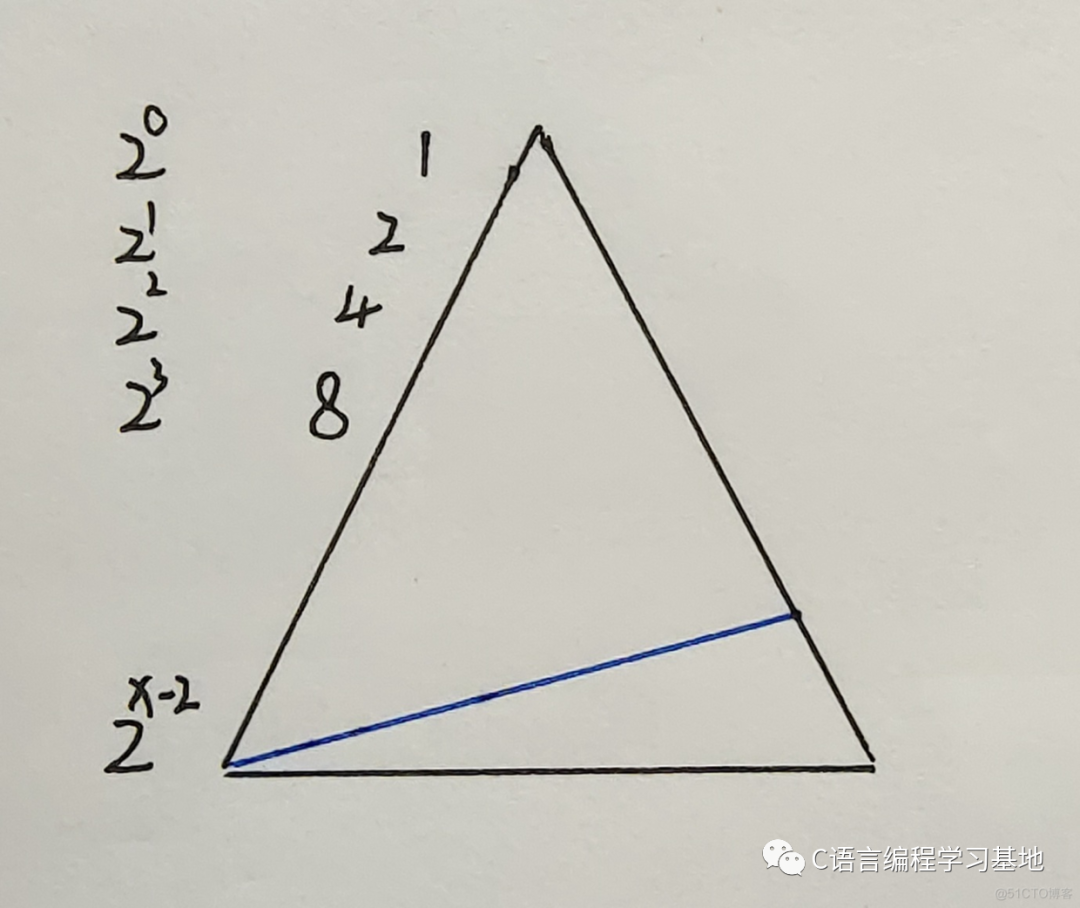
由于時(shí)間復(fù)雜度只是一個(gè)估算值,這一部分缺失的調(diào)用次數(shù)對(duì)總運(yùn)行次數(shù)的影響不大,故忽略掉
NO.9
void fun(int n){int i=l;while(i<=n)i=i*2;}
此函數(shù)有一個(gè)循環(huán),但是循環(huán)沒有被執(zhí)行n次,i每次都是2倍進(jìn)行遞增,所以循環(huán)只會(huì)被執(zhí)行l(wèi)og2n次
NO.10
給定一個(gè)整數(shù)sum,從有N個(gè)有序元素的數(shù)組中尋找元素a,b,使得a+b的結(jié)果最接近sum,最快的平均時(shí)間復(fù)雜度是?
A. O(n)//√B. O(n^2)C. O(nlogn)D. O(logn)
數(shù)組元素有序,所以a,b兩個(gè)數(shù)可以分別從開始和結(jié)尾處開始搜,根據(jù)首尾元素的和是否大于sum,決定搜索的移動(dòng),整個(gè)數(shù)組被搜索一遍,就可以得到結(jié)果,所以最好時(shí)間復(fù)雜度為n
審核編輯:湯梓紅
-
算法
+關(guān)注
關(guān)注
23文章
4630瀏覽量
93352 -
函數(shù)
+關(guān)注
關(guān)注
3文章
4346瀏覽量
62968 -
復(fù)雜度
+關(guān)注
關(guān)注
0文章
8瀏覽量
7929
原文標(biāo)題:【算法】幾分鐘時(shí)間讓你徹底學(xué)會(huì)—時(shí)間復(fù)雜度!
文章出處:【微信號(hào):cyuyanxuexi,微信公眾號(hào):C語言編程學(xué)習(xí)基地】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
時(shí)間復(fù)雜度為 O(n^2) 的排序算法

PCB與PCBA工藝復(fù)雜度的量化評(píng)估與應(yīng)用初探!
JEM軟件復(fù)雜度的增加情況
時(shí)間復(fù)雜度是指什么
各種排序算法的時(shí)間空間復(fù)雜度、穩(wěn)定性
圖像復(fù)雜度對(duì)信息隱藏性能影響分析
深度剖析時(shí)間復(fù)雜度
如何求遞歸算法的時(shí)間復(fù)雜度
如何求遞歸算法的時(shí)間復(fù)雜度
常見機(jī)器學(xué)習(xí)算法的計(jì)算復(fù)雜度
算法時(shí)空復(fù)雜度分析實(shí)用指南1
算法時(shí)空復(fù)雜度分析實(shí)用指南2
算法時(shí)空復(fù)雜度分析實(shí)用指南(上)

如何計(jì)算時(shí)間復(fù)雜度
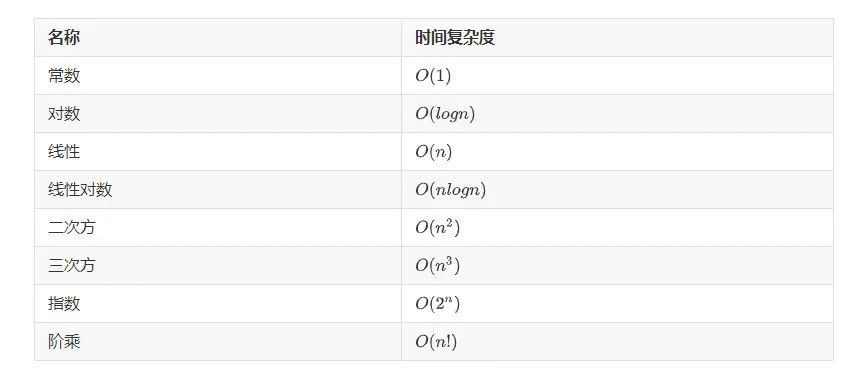




 一文徹底了解時(shí)間復(fù)雜度
一文徹底了解時(shí)間復(fù)雜度










評(píng)論