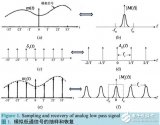
信號的抽樣我們都知道了:

圖1
上圖最后一步沖激抽樣信號的頻譜的推導用到了這個公式:
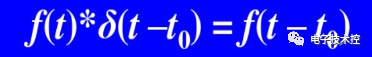
這個公式的推導可以參考:
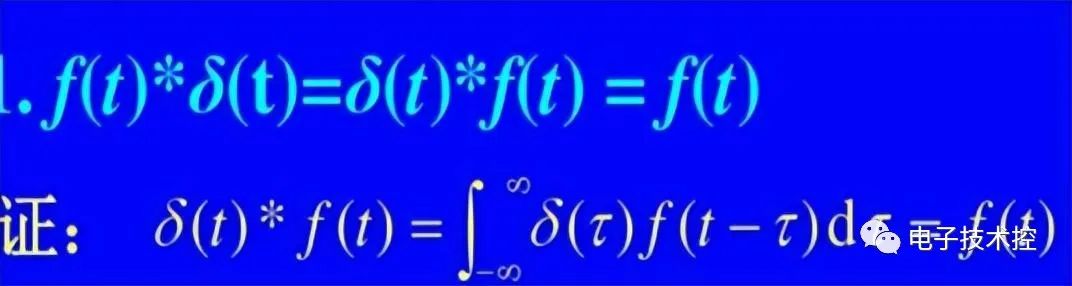
就是
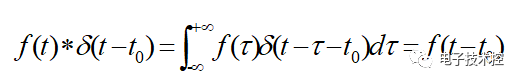
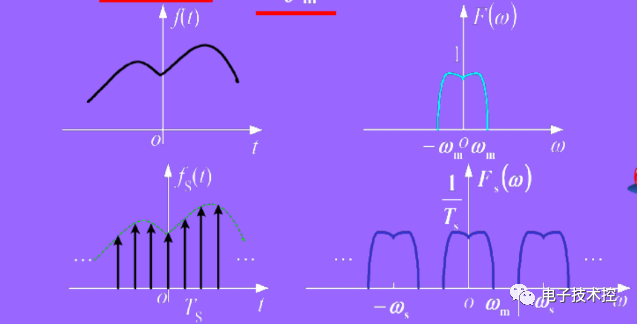
我們注意到圖1中抽樣函數的頻譜
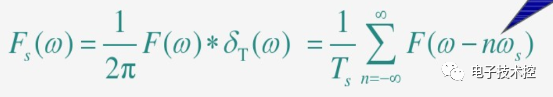
是由無窮個等間隔重復的頻譜函數F(w)組成,這就是時域的離散導致的頻域周期現象,如下圖所示:
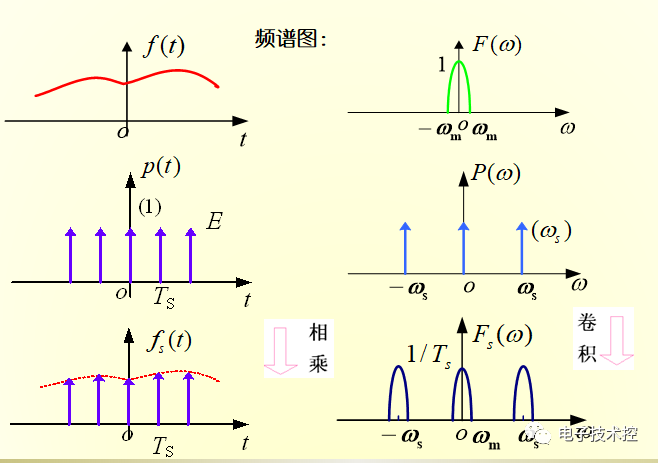
由于相同的頻譜函數等間隔重復,就由可能導致頻譜混疊現象,如下圖:
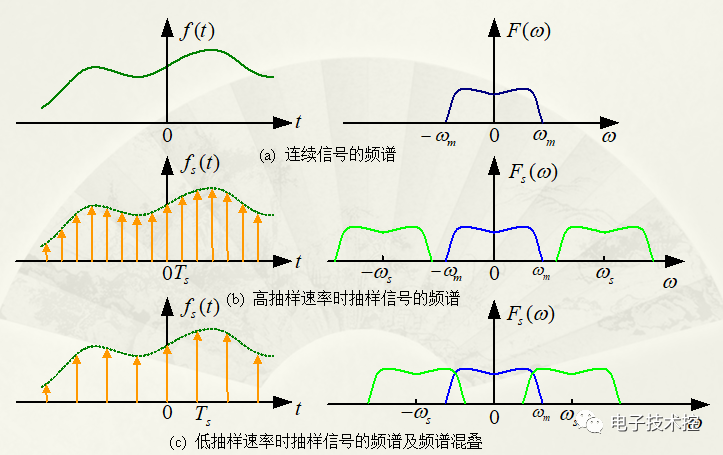
為了能由頻譜函數有效地恢復出原來的時域信號,就必須消除頻譜混疊現象。在不存在頻譜混疊的前提下,采用一個頻域中的矩形濾波器H(w)將第一個周期的頻譜函數取出,如下圖:
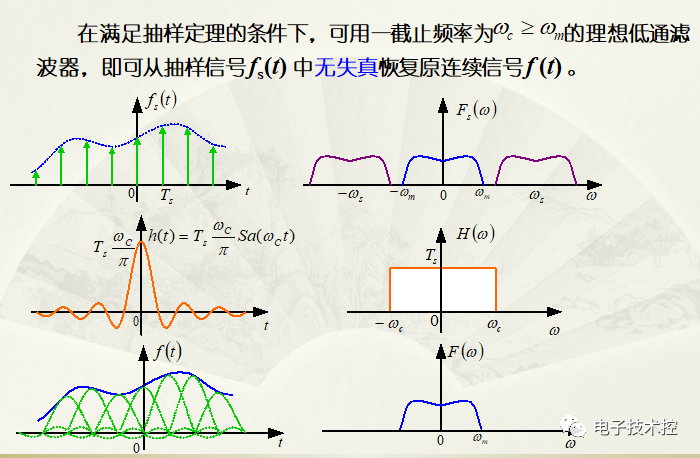
圖2
由上圖可以看到,頻域中的矩形函數,在時域中是一個sinc函數。關于門函數,我們有:
對于單個門函數:
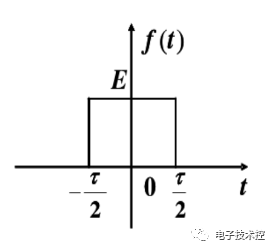
其頻譜(傅里葉變換,積分限實際上是無窮)為:

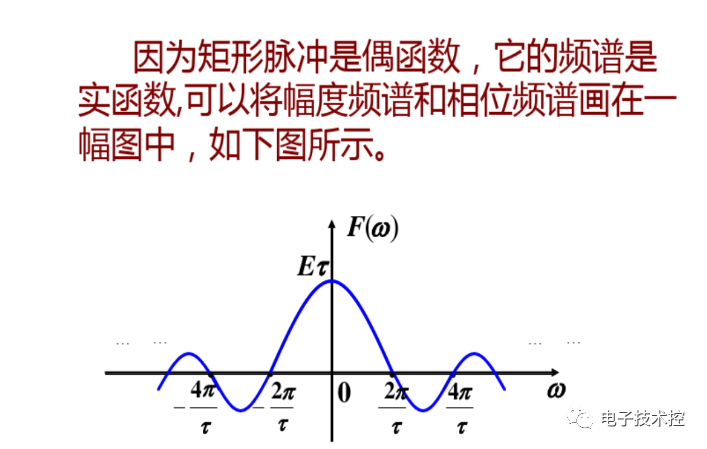
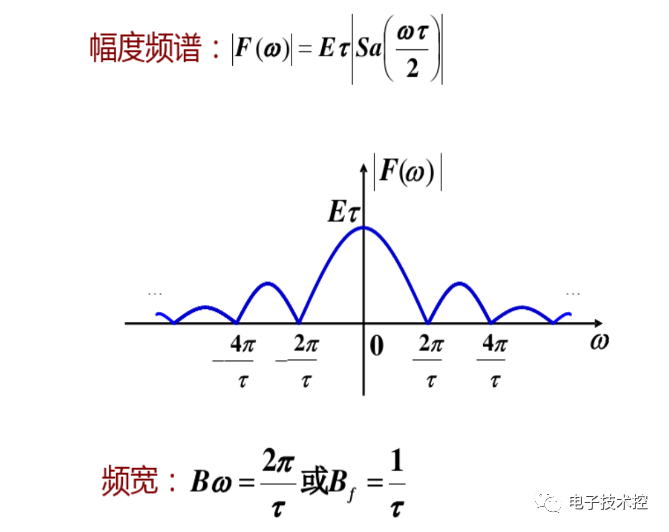
由以上分析看出,單個的門函數其頻譜函數sa是連續的非周期函數,在w=0時取得最大值1。
下面通過圖2中的低通濾波器H(w)進行信號恢復:

H(w)的時域函數為
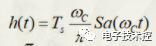
證明如下:

由于頻域的乘積
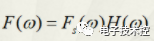
等于時域的卷積,得到:

上圖表明,恢復出的時域信號f(t)是抽樣點上的值f(nTs)與sinc(sa)函數在最大值點1(t=nTs)的乘積之和。
圖解恢復過程:

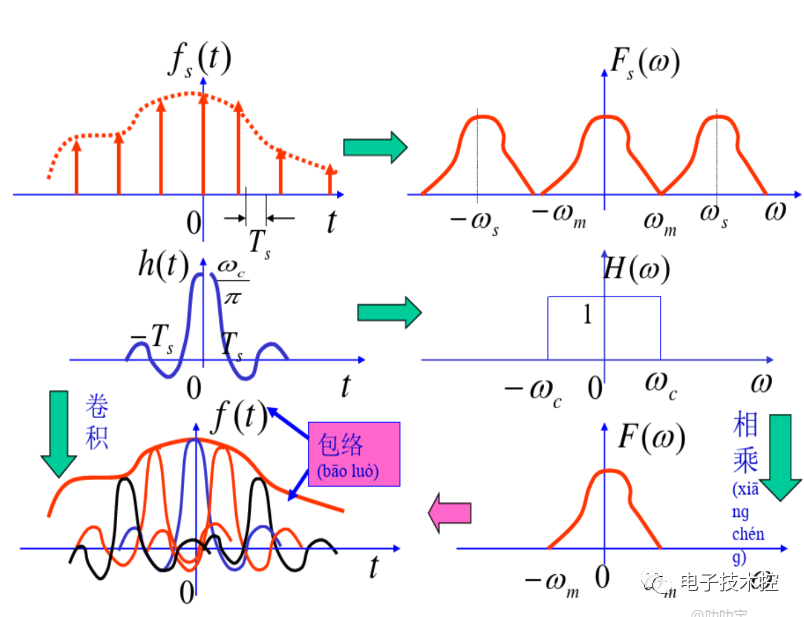
上圖表明,最后恢復出的時域信號f(t),是由一個個以nTS為中心點的sinc(sa)函數的最大值點構成的包絡線。顯然,TS越小,ws越大,恢復的效果越好。
也可以圖解如下:
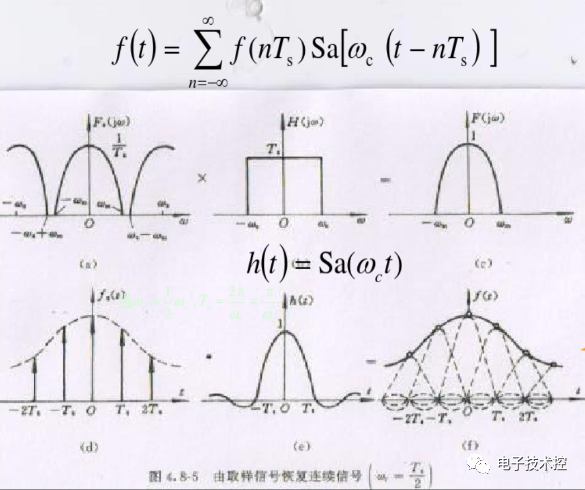
同樣可以看出f(t)的構成過程。
簡單總結:
1:時域信號抽樣以后,得到按周期拓展的頻域信號;
2:用一個頻域的低通濾波器H(w)進行濾波,得到需要恢復的時域信號的頻譜函數;
3:由于頻域的乘積等于時域的卷積,得到待恢復信號與sinc(sa)函數的關系,從而確定f(t)是由一個個以nTS為中心點的sinc(sa)函數的最大值點構成的包絡線,顯然,TS越小,恢復的效果越好。
4:恢復出的時域信號f(t)實際上是由一個個sinc(sa)函數合成。
審核編輯:湯梓紅
-
信號
+關注
關注
11文章
2807瀏覽量
77113 -
頻譜
+關注
關注
7文章
887瀏覽量
45786 -
函數
+關注
關注
3文章
4346瀏覽量
62977
原文標題:理解信號的抽樣與恢復過程
文章出處:【微信號:電子技術控,微信公眾號:電子技術控】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦


抽樣定理和脈沖調幅(PAM)實驗
抽樣定理與脈沖調幅(PAM)實驗
基于抽樣定理及信號恢復理論證明
自定義信號的抽樣與恢復并在LCD上顯示結果實現
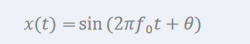




 理解信號的抽樣與恢復過程
理解信號的抽樣與恢復過程
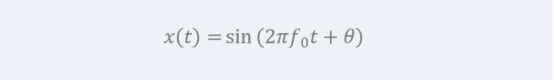
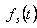










評論