摘要：為了降低面向 5G 的正交頻分復用系統的峰均功率比和計算復雜度，采用 5G 通信領域中的低密度奇偶校驗碼信道編碼方案，通過部分傳輸序列改進后的循環移位序列方法與低密度奇偶校驗碼聯合方法進行編碼，稱為 LDPCSS 碼，根據導出 LDPCSS 碼的奇偶校驗矩陣，使用置信度傳播算法進行譯碼。為了進一步降低 LDPCSS 碼的延遲和搜索復雜度，提出基于遺傳算法的 LDPCSS方法，稱為 LDPCSS?GA 方法。通過仿真與現有方法進行比較分析，結果表明，所采用的方法降低了BP譯碼器的譯碼復雜度和延遲，同時降低系統的 PAPR 和計算復雜度，還提升了誤碼率性能。

0 引 言

正交頻分復用（OFDM）采用多載波調制技術，具有高數據傳輸速率和抗窄帶干擾能力，與其他多載波技術相比，其帶寬利用率高，可增加系統容量還能提供可靠的傳輸，能適應第五代（5G）寬帶無線通信網絡[1]。但OFDM 系 統 的 主 要 缺 點 之 一 在 于 高 峰 均 功 率 比（PAPR），因 為 信 號 通 過 某 些 非 線 性 設 備 傳 播 時 ，高PAPR 可能會導致帶內失真和帶外輻射，從而導致系統誤碼率性能下降[2]。

目前，研究降低 OFDM 系統 PAPR 的方法有很多，大致可分為兩類：一類是信號失真技術[3]，如削波、濾波和星座擴展等。削波技術是將信號削波到預定的閾值以下，對于 OFDM 系統，很容易產生帶內失真和誤碼率升高，星座擴展是無失真技術，但會增加發射信號的能量。第二類包括信號加擾技術，如選擇性映射（SLM）[4]是在多信號表示方法的基礎上，具有與編碼、星座擴展相似的特性，且需要發送邊信息，會產生較高的計算復雜度和降低帶寬效率。部分傳輸序列（PTS）[5]是 PAPR降低研究最廣泛的技術，也是無失真的一種方法。由于 PTS 方法將相位因子信息作為輔助信息發送到接收機，會導致傳輸效率降低且增加了系統復雜性，文獻[6?7]采用 GA 遺傳算法對旋轉因子進行優化，PAPR 性能降低了，但在接收機上需要附加相關技術來恢復發送的 OFDM 信號。

文獻[8]采用循環移位序列（CSS）方法，CSS 方法是從 PTS 方法發展而來的，它將 OFDM 信號子序列循環移位并組合后替代 OFDM 信號序列，通過循環移位序列而不是將旋轉因子乘以 OFDM 信號子序列，不管從 PAPR降低還是系統性能上，CSS方法比 PTS方法更好。

OFDM 系統另外一個主要缺點是在衰落環境中的BER 性能差，導致接收器不可能無錯誤地檢測到所有子載波。為了減小衰落的影響，文獻[9]采用 LDPC 編碼技術實現 OFDM 系統。文獻[10]將 Turbo 編碼技術應用到OFDM 系統中，雖然 Turbo碼在編碼過程中比 LDPC 碼簡單，但在譯碼時比 LDPC 碼復雜得多，而 LDPC 碼具有較強的糾錯能力和抗突發差錯。文獻[11]采用遺傳算法（GA）優化 LDPC 碼，GA 的特點在于能解決高維優化問題，不僅能找到局部最小值，且選擇恰當的參數能很快收斂并獲得最優解，常用于人工智能、信道編碼和 LDPC譯碼器等領域。

綜上所述，本文提出了一種對 LDPC 碼和 CSS 聯合編碼的方法（稱為 LDPCSS 碼），即將 CSS 和 LDPC 碼作為前期編碼階段，然后導出 LDPC?CSS 碼的奇偶校驗矩陣，通過奇偶校驗矩陣，使用置信度傳播算法（BP）和GA 算法進行聯合譯碼。

1 LDPCSS聯合方法的編譯碼

1.1 OFDM 系統的 PAPR 計算方法

OFDM 信號由多個獨立調制的子載波組成，當相互疊加時，會產生較大的 PAPR，當 N 個信號以相同相位疊加時，所產生的峰值功率是平均功率的 N 倍，在時間間隔 τ中傳輸的信號 x ( t )的 PAPR 定義為：

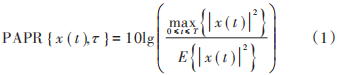
式中：max { ? }表示峰值信號功率；E { ? }表示平均信號功率。為了計算更精確的 PAPR 值，應考慮更多符號，否則可能會省略一些峰值，從而導致 PAPR 值錯誤，可通過對 x ( t ) 進行過采樣來解決，用互補累計分布函數（CCDF）定義峰均值超過某一門限值的概率：

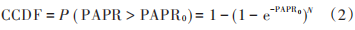
式中 PAPR0表示某個限幅電平的 PAPR 值。

1.2 基于 LDPCSS?GA 的 OFDM 系統

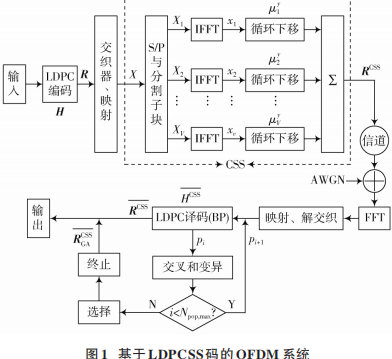
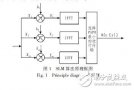
在 LDPCSS?GA 的 OFDM 系統中（如圖 1所示），一個LDPC 碼字通過 PSK 調制和 QAM 映射到 OFDM 子載波上，經隨機交織器后，將行向量 R表示的 LDPC 碼字映射到子載波數為 N 的一個 OFDM 數據塊上。然后將 X 劃分為 V 個不相交的子塊，經 IFFT 變換后得到時域序列。

不妨令 N和 V為 2的整數冪且分割滿足條件 Xv ( k ) = 0或∑v=1VXv = X，k = 1, 2,?,N，則 CSS 候選數據子塊 XCSS 表示第 V 個 OFDM 信號系列經循環下移與求和組合后得到第 y（1 ≤ y ≤ Y）個 OFDM 序列[12]為：

式中，xyv 表示xv通過整數μyv循環左移，即：

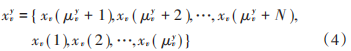
式中：μyv表示偏移值；對于第y 個 OFDM序列滿足：-μy ={ μy1, μy2,?, μyV}，-μy 表示第y 個備選OFDM信號序列的偏移值集合。

由文獻[12]可知，循環移位操作不會破壞輸入符號序列之間的正交性，因時域中的循環移位等效于在頻域中乘以相應的線性相位矢量。因此，當獲得校驗矩陣 H后，可根據校驗矩陣 H 進行編碼，從而得到相應的碼字R，Rv ( v = 1, 2,?, V ) 表示循環移位后的行向量，經 CSS處理后，原始的LDPC碼字R被分割為V個向量，即R1，…，RV，長度為 N（vv = 1, 2,?, V），并得到相對應的行向量(RCSS) v，表示為( RCSS) 1，( RCSS) 2，…，( RCSS) V。根據 CSS和以上假設，則：

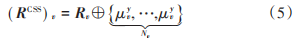
式中 ⊕ 表示模 2加法運算。

本文將 RCSS 作為等效傳輸碼字，將 LDPCSS 碼字定義為由等效傳輸碼字和循環移位組成的碼字。

定義 1：先前描述的 OFDM 系統的 LDPCSS 碼是具有以下碼字的分組碼，它的矢量表示為：

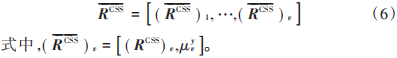
根據文獻[11]和式（3）、式（4），不妨設 y=2，則由兩個偏移集 μˉ 1 和 μˉ 2 生成的備選序列由 ( RCSS) 1 和 ( RCSS) 2 表示，不失一般性，令( RCSS) 1 為不受 CSS 處理影響的行向量，由全零偏移集 μˉ 1 = { 0, 0,?, 0 }生成為：

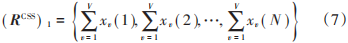
同理，( RCSS) 2通過偏移集μˉ 2 = { μ21 , μ22 ,?, μ2V}生成為：

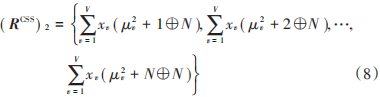
1.3 PAPR 減小和 LDPCSS?GA 算法

本文減小系統 PAPR 值采用文獻[12]的交織分區以及制定的標準 2生成的偏移集，如果滿足：

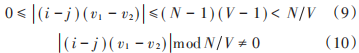
其中：1 ≤ v1 ≠ v2 ≤ V，1 ≤ i ≠ j ≤ N，N 表示子載波數，V 表示子塊數，且滿足 N = WV - 1，W 為旋轉因子數。考慮 LDPCSS 碼的優化問題，在設計過程中，盡量降低系統 PAPR、誤碼率和復雜度，因此應用了遺傳算法。遺傳算法是一種常用的函數優化方法，它具有全局搜索能力，可獲得最佳或更好的近似解。LDPCSS?GA 算法基本思想如下：

1）初始化：種群大小 p，編碼率 Rc，碼長 N，設置最大迭代次數 N max, pop。2）for i = 1, 2,?,N max, pop do

3）更新種群：將父代向量 H1 的第一行與父代向量H2 的第二行相結合生成下一代向量 H1，交叉率 pc = 1。將下一代的隨機位置上 0 → 1生成為 H1a，突變率 pm = 1。為了恢復編碼率 Rc，對產生的后代向量 H1a進行突變，產生向量 H1b作用于群體，并更新種群。

4）計算適應度函數：LDPC譯碼是基于Tanner圖的消息傳遞迭代譯碼，采用置信傳播譯碼算法（BP）沿Tanner圖的邊傳遞概率值，對位節點的判據采用其概率值組合。

5）計算 BER：初始化 BER 并對每次輸入-----RCSS 的種群大小進行更新，采用 BP算法并更新 BER。

6）end for

7）選擇最優向量-----RCSSGA 輸出。

8）結束

本文將每次更新的最佳-----RCSS 向量作為新種群的成員，雖然收斂速度減慢，但能確保收斂到局部最優值，并通過不斷進化保證目標函數的單調性，以便觀察候選解。

2 仿真分析

通過概率密度演化方法[13]得到最大變量節點度分布，并構造和優化奇偶校驗矩陣H，仿真中發射機不發送循環移位序列，接收機采用 BP算法。

圖 2顯示了不同方法降低系統PAPR的性能比較，相關的參數設置見表1。在 CCDF 為10-3時，本文采用的LDPCSS聯合方法降低系統PAPR 約 5.7 dB，相比文獻[9]方法降低約0.1 dB，且明顯優于其他方法。

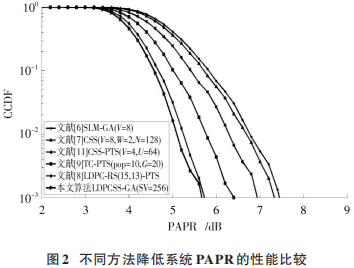
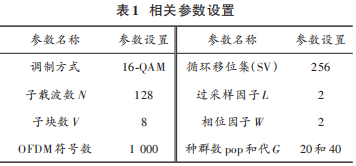
圖 3顯示了不同方法的 BER性能，為了與文獻[9?10]的BER性能比較，設置碼率為1 2，約束長度為4，輸入回退為3，N =512，在AWGN 信道中采用16QAM，可以看出，本文采用的方法在傳輸信號的 PAPR 值較大時，BER 性能下降很小，隨著子載波和星座數增加，BER 性能明顯優于文獻[9?10]方法。

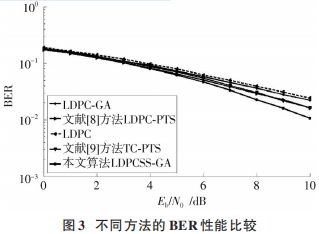
圖 4 顯示了原始 OFDM 信號和采用 CSS 處理后 ，當子載波數 N=8，16，32 和 64，CCDF=10-3 時，經過 CSS處理后的 PAPR 分別降低了約 6.2 dB，6.6 dB，7.1 dB 和7.7 dB。

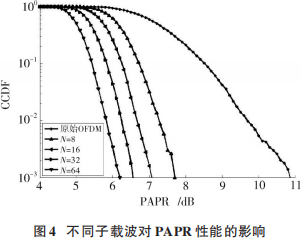
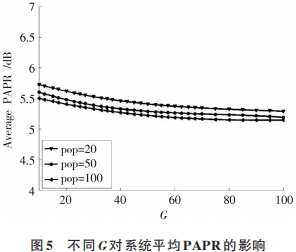
圖 5 顯示采用 LDPCSS?GA 方法的 PAPR 平均值分析，其中種群大小設置為 20，50和 100，G 在 10~100之間取值，可以看出種群數在 20~100 時，平均 PAPR 的值相差 0.2 dB，顯然種群數為 20比較合理。

3 結 語

本文提出了一種基于 LDPCSS 碼的奇偶校驗矩陣，并使用 BP 算法對 LDPC 碼字和循環移位因子進行聯合譯碼，通過 GA 算法不僅降低了 OFDM 系統的 PAPR，且經過優化后的 LDPC 碼，既降低了 BP譯碼器的譯碼復雜度和延遲（因為不需要傳輸輔助信息即循環移位因子，也不需要在譯碼前對其進行估計），又在誤碼率性能方面得到了提升。仿真結果表明，本文所采用的 LDPCSS?GA 方法與其他方法比較，有效降低了 PAPR 和計算復雜度。由于需要進一步降低了 PAPR，因此，在未來研究中，如何提高譯碼的收斂速度且不降低糾錯能力仍是一項重要的工作。

審核編輯：湯梓紅