引 言

線性調頻信號（LFM）在時域和頻域上具有理想的多普勒頻移和良好的壓縮性能，近年來，成為低截獲概率雷達信號的一種重要形式，在雷達、聲吶及通信等多領域得到了非常普遍的應用。在電子對抗領域中，有許多重要的任務，如電子偵察和電子干擾，可以通過攔截敵方雷達信號和從 LFM 信號中提取參數信息來實現。因此，LFM 信號參數能否準確估計在頻譜估計中顯得至關重要。

目前，國內外學者在 LFM 信號的參數估計領域做了許多的研究，從時域和頻域方面提出了一些可行的參數估計方法。文獻[4]提出了基于霍夫變換短時傅里葉變換（STFT）的單源時頻域點選擇算法，克服了現有算法對頻譜重疊 LFM 信號的局限性；文獻[5]提出基于自適應粒子群優化（APSO）算法的分段重構（SR）方法，對每個信號部分變換后實現 SR，同時利用互相關指數來表示系統的性能，在信號增強和噪聲抑制方面有較好的性能；文獻[6]將盒維數理論引入到 LFM 參數估計中，通過探討信號參數與盒維數的關系來實現參數的估計。但是上面的方法都在一定程度上增加了計算復雜度。文獻[7]采用稀疏傅里葉變換，試圖從不同的角度降低運算量，但最優旋轉角度的判定與選擇沒有給出定論；文獻[8]引入了正交匹配追蹤算法，提出了一種估計分數階帶限 LFM 初始頻率和最終頻率的改進優化算法，但是由于算法所要求的前提條件較多，對信號的估計有一定的限制；文獻[9?10]提出將基本粒子群算法用于基于分數階傅里葉變換的 LFM 信號參數估計中，通過改進最優階次的搜索問題提高了精確度，但本質仍是基于二維峰值搜索的方法，存在計算量和估計精度之間的矛盾。

由于實際的雷達接收機工作時會受到外界環境的影響，因此，本文針對在混合信號中輻射源信號的參數估計問題進行研究，建立輻射源 LFM 相參脈沖串信號模型，提出一種基于二階振蕩粒子群算法和分數域展寬法（W?FRFT）相結合的參數估計方法。通過判斷鑒相脈沖幅度的變化來識別信號的相參性，區分目標輻射源的信號，在此基礎上利用粒子群最優值算法對積累后的信號計算最小分數域展寬值得到 FRFT 的最優階次，從而求得信號參數。與傳統方法相比，本文所提方法解決了最優階次的精確與否受限于搜索間隔的問題，使精確度和計算復雜度在一定程度上得到了改善。

1 相參脈沖串信號模型

對于接收機接收到的脈沖串信號，可以視作是在不同時刻對連續波信號加以線性調制。接收的 LFM 信號的離散數學模型表示為：

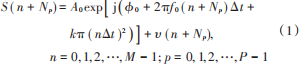
式中：P 為脈沖總個數；f0 為起始頻率；A0 為接收信號的幅度；M 為單個脈沖內采樣點個數；k 為調頻斜率；?0 為恒定的初始相位；Δt 為采樣間隔；Np為第 p 個脈沖重復周期內的采樣點；υ 為復高斯白噪聲干擾信號，實部與虛部噪聲相互獨立，假設信號為單一重頻、幅度不變的線性調頻信號。

2 雷達目標輻射源信號識別

在多信息源和多傳感器的復雜環境中，目標輻射源的信號往往會受到其他輻射源的干擾或者噪聲的影響，需要從測量到的混合信號中提取出目標輻射源信號，進行參數估計，提取有用信息。

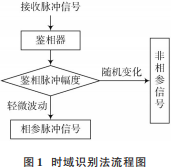
雷達輻射源發射的相參脈沖串信號之間的相位具有一致性或連續性，如果脈沖 1 和脈沖 2 來自于同一雷達輻射源，則兩個脈沖是相參的，即脈沖 1和脈沖 2的雷達輻射源的初始相位相同[11]；否則，脈沖之間的初始相位不同且信號是非相參的。因此可以根據此理論利用鑒相器的特性，采用時域識別法判別混合信號中的輻射源信號。

假設輸入的第 m 個脈沖信號為：

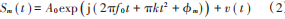
延遲 M 時間后，信號變為：

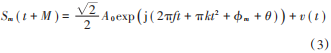
式中，由于延遲造成的附加相位 θ = 2πfM。設延遲時間 M 等于一個脈沖重復間隔，因此當 Sm變成 Sm ( t + M ) 時，原信號 Sm 的下個脈沖剛好到達混頻器：

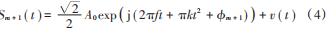
當式（3）和式（4）中 2 路信號進入混頻器后，對此進行共軛相乘運算，共軛相乘后的信號經過低通濾波器。

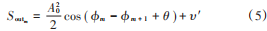
由于相參脈沖信號滿足初始相位均相同的特性，因此，若是來自同一輻射源的相參信號，則鑒相器輸出的鑒相脈沖幅度的實部為：

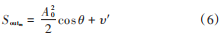
由于輸出的幅度實部與延遲造成的附加相位 θ、幅度 A0 和噪聲項有關，而前兩者均為恒定不變的值，因此P 個脈沖組成的脈沖串輸出的 P-1 個鑒相脈沖幅度僅僅噪聲組合項不同，而噪聲是均值相同的高斯白噪聲，所以式（6）輸出的幅度近似相同，脈沖幅度在 0.5上下輕微波動。而若脈沖串為非相參的脈沖信號，相位差為一個周期內的隨機量，則鑒相脈沖幅度會隨著相位差的隨機變化而在 0~0.5 范圍內波動起伏，且有明顯峰值。信號相參性時域識別法的具體識別流程圖如圖 1所示。

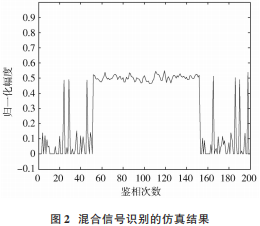
以一個混合信號脈沖串為例，其中前 50 個脈沖和后 150個脈沖為非相參信號，51~149個脈沖為來自目標輻射源的相參信號。

如圖 2 仿真曲線所示，脈沖串信號通過鑒相判別，將相參信號和非相參信號通過幅度值范圍區分開來，可以看出，非相參信號脈沖串幅度值不僅波動范圍大，而且有明顯峰值，而相參信號脈沖串幅度值一直呈現平穩狀態，證明此方法對于識別目標輻射源相參信號有效。通過對接收到的混合信號進行判別，可以準確獲得目標輻射源的信號，有利于后續的參數估計，獲得有效信息。

3 目標輻射源信號的參數估計

3.1 LFM 信號的 FRFT表示

在第 2 節中通過對混合脈沖信號進行時域相參識別的處理，分離得到輻射源相參脈沖信號，對該脈沖信號進行時域積累后進行參數估計。假定時域積累后脈沖寬度內的 LFM 信號的復數表達式如下：

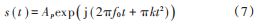
s ( t )的 FRFT的定義式為：

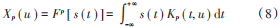
式中：p 是 FRFT 階次；Fp 是 FRFT算子；Kp(t,u)是 FRFT核[12]，表示為：

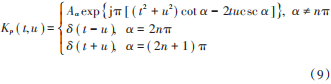
式中 Aα = 1 - jcot α ，α = pπ 2 為時頻平面的變換角度，取值范圍可以為任意實數。

LFM 信號在變換域上的分布如圖 3所示。

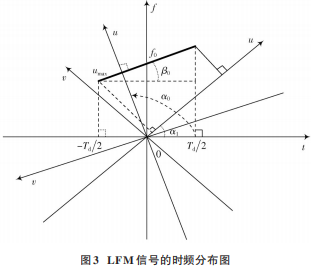
在圖 3 中，黑色斜線表示 LFM 信號的時頻分布線，β（0β0 ∈ ( 0, π 2 ) 或 β0∈（π 2，π））為時頻線與 t 軸的夾角，u ⊥ v 軸表示時、頻軸逆時針旋轉 α 角度，此處取 α∈[0，π]，由 α 和 p 的變換關系可得 p∈[0，2]。隨著旋轉角度α 的變化，FRFT 會形成一個時頻平面的變化，且不同的旋轉角度會帶來不同的聚集特性，包括頻譜在分數域內的寬度、頻譜的幅值等，但不變的性質是信號只在其匹配的最佳分數域內出現頻譜尖峰。

3.2 基于 FRFT的分數域展寬（W?FRFT）

由于 LFM 信號觀測時長為 Tp，信號的時頻線與時間軸 t的角度為 β0，則 LFM 信號的時頻線長度 ρ為[13]：

由式（10）可知，信號參數 Tp 和 β0 已知時，時頻線長度 ρ 是一個常量。當時頻線在分數域上旋轉 α 角度后，在 u 軸上的投影為 ρα，即分數域展寬值。此時設時頻線與 u 軸的夾角為 θ=β- α，其中取 β∈（0，π 2），此時，信號的分數域展寬值為：

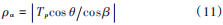
因此，當信號確定時，LFM信號的分數域展寬值是一個僅與旋轉角度α相關的值。α角度的變化影響時頻線在 u 軸的投影，當 α = β 時，ρ?u，此時，ρα 取得最大值；當 α =β+π2時，ρ ⊥ u，ρα 取得最小值，且 ρα趨近于0，此時α為最佳旋轉角度，對應的p為最優階次。

文獻[14]中為保持時域和頻域上的一致性，降低精度誤差，需要對 LFM 信號進行歸一化處理，設維度歸一化因子為S=(Tpfs1 2)，則初始頻率和調頻斜率的估計值為：

3.3 降低分數階次以減小計算量

根據式（12），可得：

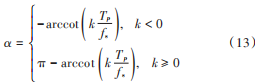
由奈奎斯特采樣定理可得，采樣頻率 fs 至少是帶寬B 的 2 倍，為了得到無失真的原始信號，采樣頻率 fs 必須滿足[15]：

將式（14）代入式（13）可得：

由于 α = pπ 2，所以式（15）可化為：

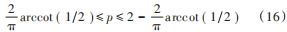
因此，FRFT 階次 p 從[0，2]縮小到[0.7，1.29]，與傳統的 FRFT方法相比，節省了 2 3左右的計算量。

4 基于二階振蕩粒子群算法和W?FRFT的LFM信號參數估計方法

基于 W?FRFT算法進行最優階次 p求解時，需要對 p進行搜索，搜索間隔越小，誤差越小，估計精度越高，則所需時間越長，反之，則造成參數估計誤差越大。因此，本文通過粒子群算法對基于分數展寬原理的參數估計進行改進，避免因搜索間隔問題而不能準確找到最優解的情況。以分數域展寬值為目標適應度函數，以階次[0.7，1.29]為位置范圍，在位置范圍內尋找最小分數域展寬值，從而得到對應的最優階次。

標準粒子群算法中種群進化是由粒子的速度公式和位置公式組成：

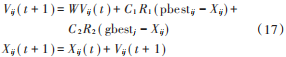
式中：Xij 和 Vij 分別是第 i 個粒子所處的位置和速度的第 j 維；pbestij 為第 i 個粒子在歷史最優位置時的第 j 維；gbestj 為全局最優位置的第 j 維[16]；W 為慣性權重；C1 和C2 分別為調節粒子自身最優位置和全局歷史最優位置靠近的權重；R1和 R2為相互獨立的隨機數。

但是標準粒子群算法中所有粒子的更新僅僅依靠它的個體最優位置和全局最優位置，并沒有考慮到粒子個體之間及粒子位置變化對它自身的影響，使得粒子沒有充分利用有效信息。

本文將改進的二階振蕩粒子群算法引入到信號處理中，針對分數域中最優階次的搜索進行改進，改進后的粒子群算法的迭代公式如下：

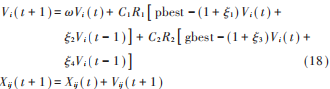
這里的 ξi, i = 1, 2, 3, 4 雖然是隨機數，但是取值是有限制的，設最大迭代次數為Gmax：

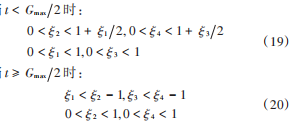
同時，為了防止后期局部搜索能力變差，陷入局部最優等問題，對慣性權重進行改進[17]，并表示為：

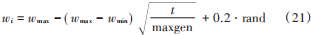
式中 maxgen 為最大迭代次數。改進后的參數估計算法充分利用了所有粒子的最優位置的有效信息及同一粒子的位置變化信息，更加精確地搜索到最優階次，避免了搜索間隔帶來的誤差，同時，減小了計算量，進一步提高了算法的優化性能。

基于二階振蕩粒子群算法與 W ?FRFT 相結合的優化算法流程如下：

1）在混合信號中根據雷達輻射源發射信號的相參性識別出目標輻射源的信號；

2）經過時域積累后的信號在縮小后的階數范圍[0.7，1.29]內，初始化粒子的位置并計算粒子的適應度值，即分數域展寬值；

3） 尋 找 粒 子 的 全 局 極 值 并 更 新 粒 子 的 位 置 和速度；

4）判斷是否滿足精度要求和迭代次數，如果不滿足，則回到步驟 3）；

5）若適應度值滿足精度要求和迭代次數，則輸出最小適應度值即最小分數域展寬值和最優階次，根據式（12）計算初始頻率 f和調頻斜率 k。

5 仿真實驗與結果分析

本文以接收寬帶 LFM 信號為例，其初始頻率 f0 =100 MHz，采樣頻率 fs =2.4 GHz，振幅 Ap = 1，脈沖寬度Tp=1 μs，帶寬 B =500 MHz，調頻斜率 k = B Tp。

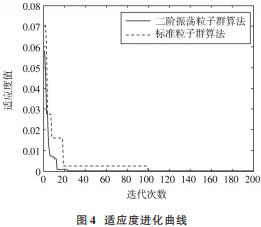
分別對兩種粒子群算法改進的參數估計算法進行比較：二階振蕩粒子群優化算法中選取粒子數為 50，迭代次數為 200；標準粒子群優化算法選取粒子數為 60，迭代次數為 200，其他參數均相同。

從圖 4 中可以看出，即使在粒子數較少的條件下，振蕩粒子群算法在迭代 22 次左右就已經趨向于穩定，而標準粒子群算法在 100 次之后才能達到近似相同的適應度值。

在高斯噪聲條件下，分別對不同的算法進行計算精度分析。在信噪比為-15~5 dB 范圍內，分別采用峰值搜索、標準粒子群算法與二階振蕩粒子群算法進行參數估計，每間隔 1 dB 進行 100 次蒙特卡洛仿真實驗，計算參數估計的均方誤差，衡量算法的計算精度。其中，相對誤差的定義為：

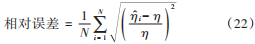
式中：η 和 ηi分別為參數實際值和第 i 次的估計值；N 為蒙特卡洛實驗仿真次數。

調頻斜率和初始頻率的均方根誤差與信噪比的關系分別如圖 5和圖 6所示。

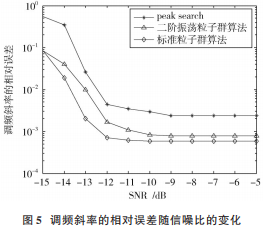
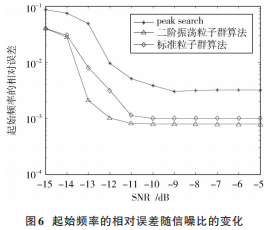
在低信噪比時，二維峰值搜索算法比較依賴于信噪比，相對誤差較大，隨著信噪比的增加，在高信噪比時相比于改進的算法有較小的相對誤差。文獻[9]中基于粒子群算法和 FRFT 的算法相對于傳統算法有一定的改進，但是基于二階振蕩粒子群算法和 W ?FRFT 的算法在低信噪比時的相對誤差更低，且測量誤差在千赫茲以內。由于幅相失真條件更復雜，參數估計性能會下降。

6 結 論

針對混合信號中的目標輻射源的識別和參數估計精度與搜索間隔存在矛盾的問題，本文提出一種二階振蕩粒子群算法與 W?FRFT 算法相結合的 LFM 信號檢測方法。仿真結果表明，本文方法可以準確識別出輻射源的信號，且當其他實驗條件相同時，在信噪比為-9 dB的條件下，相比于其他粒子群改進算法，本文算法的迭代過程能更快趨向于穩定，且相對誤差與峰值搜索算法相差 10-1數量級。

審核編輯：郭婷