在上一篇文章中,我們得到了三相逆變器的數(shù)學模型,接下來就是進行控制器的設(shè)計。其實對數(shù)學模型的設(shè)計目的就是研究控制器,控制器才是決定我們逆變結(jié)果的直接決定因素。
同時這一篇文章雖然是控制器的設(shè)計,但是對數(shù)學模型的要求也比較高,所以如果對數(shù)學模型的理解不太深入的話,可以參考上一篇文章。
基于PI雙閉環(huán)解耦控制的三相SVPWM電壓型逆變器(1)--數(shù)學模型
淺述各個坐標系的特點
有人可能會有疑問,在上一篇文章中,我們得到了許多坐標系下的數(shù)學模型,對于控制器的設(shè)計,到底用哪一種呢?實際上不同坐標系下的數(shù)學模型都是用來描述逆變器,可能有的數(shù)學模型可能有一些抽象,不利于我們理解,這些坐標系下的數(shù)學模型都有各自的特點。
在abc坐標系下,可以看出,他對數(shù)學模型的描述比較充分,足足有6個方程,三個KVL,三個KCL,這些方程是直接通過KVL,KCL定律推出來的,所以說比較容易理解,對逆變器的描述也比較直觀。
在αβ坐標系下,最大的優(yōu)點就是減少了方程的數(shù)量,將6個方程簡化為4個方程,對于控制系統(tǒng)的簡化,是一個比較好的轉(zhuǎn)換。
在dq坐標系下,方程的數(shù)量雖然沒有減少,但是因為坐標系是旋轉(zhuǎn)的,所以把交流量轉(zhuǎn)換成了直流量,有利于PI控制。從某個角度上來講,因為使用的是PI控制,所以要進行Park變換。
這三種坐標系層層遞進,最后dq坐標系是我們進行控制器設(shè)計的直接依據(jù)。下面是dq坐標系下的數(shù)學模型。
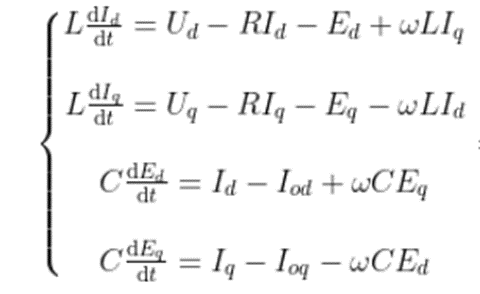
拉普拉斯變換
如果要對控制器設(shè)計,離不開的就是拉氏變換,我們首先要對上式進行拉氏變換。得到以下4個公式。
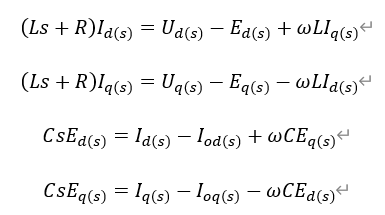
得到上面的傳遞函數(shù)之后,可以畫出系統(tǒng)框圖
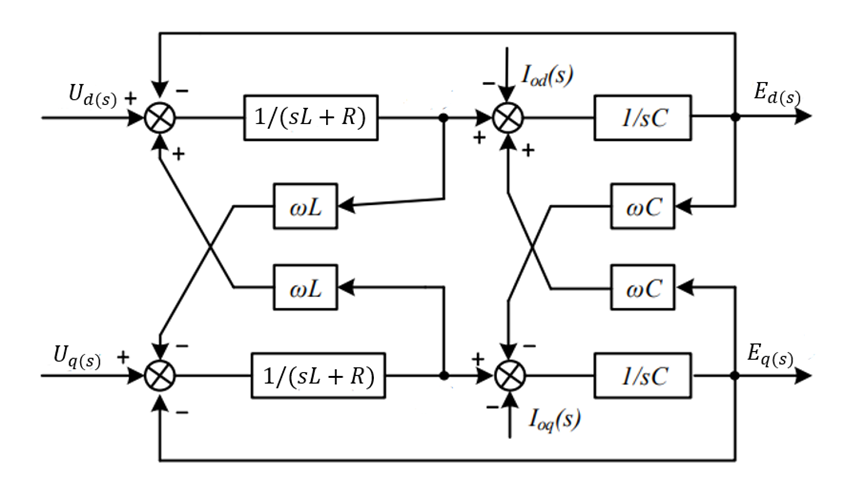
這個圖和控制系統(tǒng)框圖實際上是反過來的,因為我們是通過輸出電壓去調(diào)整輸入電壓。
從上面的結(jié)構(gòu)圖也可以看出來一個比較重要的問題,就是耦合。d和q軸是耦合在一起的,這時候就需要解耦控制,也比較簡單。
引入PI控制器
這時候我們需要把PI控制引入到這個系統(tǒng)當中。對于電壓外環(huán),令
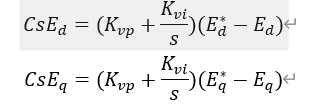
可能很多人看到這里會有些糊涂,為什么等式左邊會等于等式右邊。在等式左邊對電壓的微分實際上表示的是電流,等式右邊的PI環(huán)節(jié),對輸出電壓目標值與實際值之間做差然后經(jīng)過PI運算得到的也是電流,所以可以相等。對PI的參數(shù)進行調(diào)節(jié),可以達到微分的效果。(這里解釋的比較模糊我感覺,我對這個地方的理解也比較有限)
將這種等效關(guān)系與之前得到的時域下的數(shù)學方程相結(jié)合,可以得到下面的式子
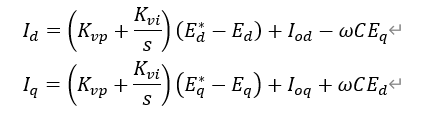
這里的Id,Iq實際上就是電流內(nèi)環(huán)的目標值,既Id*,Iq*。
對電流內(nèi)環(huán),經(jīng)過同樣的過程,就可以的類似的方程,如下所示
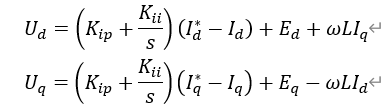
通過以上這四個方程,我們就得到了需要控制器,對應的流程圖如下
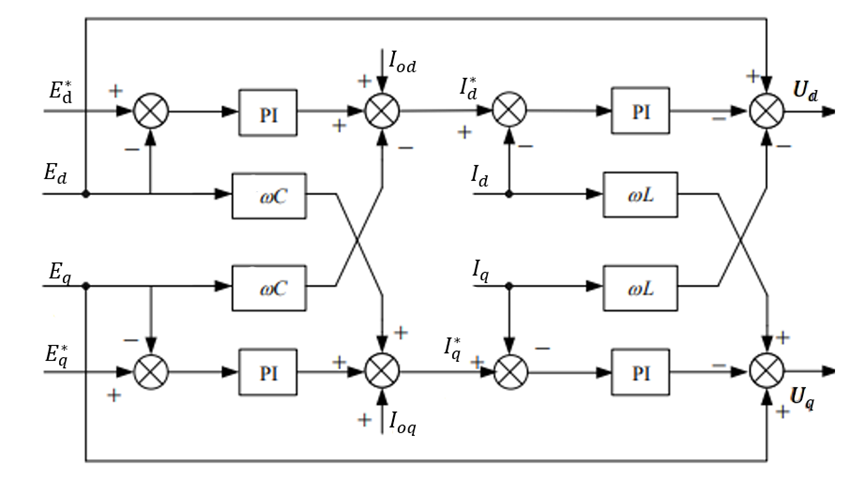
值得一體的是,通常電壓外環(huán)的輸出不去加負載電流,而是直接作為電流內(nèi)環(huán)的目標值,也可以達到控制效果。
這時候我們只是得到了控制器,并沒有計算出PI相關(guān)參數(shù),可以利用自控的相關(guān)知識進行相關(guān)計算,簡化調(diào)參,也可以直接調(diào)參。
審核編輯:湯梓紅
-
控制器
+關(guān)注
關(guān)注
112文章
16448瀏覽量
179471 -
三相逆變器
+關(guān)注
關(guān)注
3文章
91瀏覽量
18990 -
SVPWM
+關(guān)注
關(guān)注
14文章
614瀏覽量
90731 -
電能變換
+關(guān)注
關(guān)注
1文章
7瀏覽量
1281
發(fā)布評論請先 登錄
相關(guān)推薦
基于PI雙閉環(huán)解耦控制的三相SVPWM電壓型逆變器(1)--數(shù)學模型
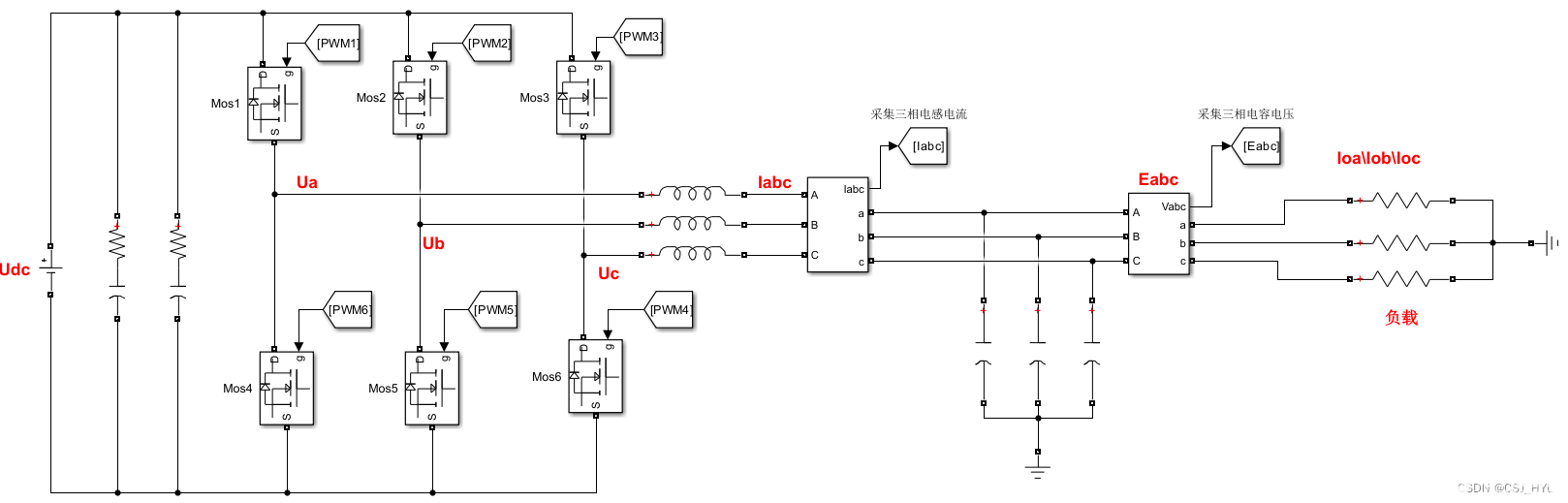
三相逆變器電壓閉環(huán)控制仿真
基于分類算法的雙三相感應電機SVPWM
MATLAB三相LCL濾波型PWM逆變器仿真設(shè)計
如何設(shè)計具有前饋解耦控制的PWM整流器雙閉環(huán)控制系統(tǒng)及仿真資料說明
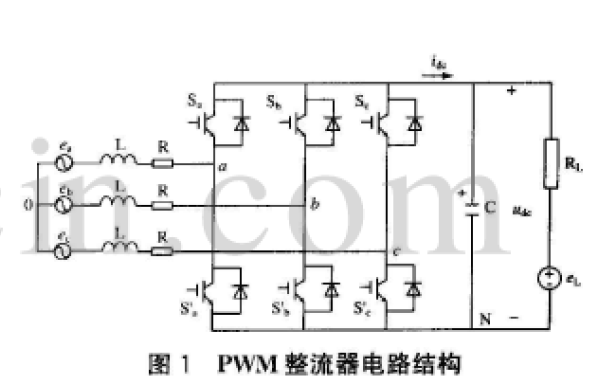
采用雙閉環(huán)PI和重復控制方案實現(xiàn)三相逆變器設(shè)計并進行仿真分析
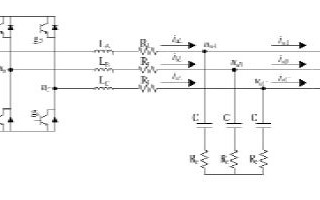
三相電壓型逆變器電壓閉環(huán)控制的Simulink仿真資料免費下載

三相逆變器雙pi控制器參數(shù)如何調(diào)節(jié)_空間矢量LCL三相逆變器





 基于PI雙閉環(huán)解耦控制的三相SVPWM電壓型逆變器(2)--控制器設(shè)計
基于PI雙閉環(huán)解耦控制的三相SVPWM電壓型逆變器(2)--控制器設(shè)計










評論