01導讀

目前光纖形狀傳感重構誤差通常表示為歐幾里得距離。然而，形狀重構的歐幾里得距離誤差取決于待重構形狀的復雜度，而形狀復雜度取決于長度、曲率和撓率。

天津大學丁振揚副教授團隊基于Frenet-Serret框架和誤差傳遞理論，建立了光頻域反射（OFDR）中分布式形狀傳感的重構誤差模型，闡明了重構誤差與曲率、撓率、光纖長度和應變測量誤差等參數之間的關系。

通過基于OFDR的分布式光纖形狀傳感系統實驗驗證了所提出的重構誤差模型的可行性和適用性。

當需要重構形狀的曲率、撓率、光纖長度的估計范圍以及OFDR系統的應變測量誤差已知時，所提出的重構誤差模型可預測最大重構誤差，進而判斷形狀重構誤差是否滿足要求實際應用的需求。

封面圖形狀重構誤差傳遞模型 圖源：Optics Express

02研究背景

近年來，光纖形狀傳感已成為光纖傳感領域的一個熱門研究方向。與其他形狀重構技術相比，光纖形狀傳感具有一系列優點，如結構緊湊、靈活性高、耐惡劣環境和腐蝕，并且能夠實現分布式傳感。光纖形狀傳感在醫療器械、機器人、航空航天等領域具有巨大的應用潛力。 目前光纖形狀傳感重構誤差通常表示為歐幾里得距離。

光纖形狀傳感重構誤差模型研究相對有限。盡管已有研究者對光纖形狀傳感精度進行了研究，但只給出單一數值，而形狀傳感精度與形狀參數（如曲率、撓率、長度和應變測量誤差）是直接相關的，單一精度值并不能反映其在任意形狀下情況。而目前歐幾里得距離誤差與形狀參數之間的模型尚未進行研究。

如果建立了重構誤差模型，則可以基于應變測量誤差和形狀參數來估計任意形狀的重構誤差，這對于根據形狀軌跡確定形狀重構誤差是否符合實際應用要求非常有用。

03創新研究

3.1 形狀重構誤差模型

分布式應變測量是形狀測量的基礎和前提。顯然，更好的空間分辨率和更高的應變測量精度將導致更精確的形狀重構。事實上，光纖形狀傳感中OFDR的感測空間分辨率通常基于OFDR系統的信噪比（SNR）設置為最小值，并且在這種情況下，空間分辨率對重構誤差的影響可以忽略不計。

因此，建立形狀重構誤差與應變測量誤差之間的三維形狀傳感誤差模型具有重要意義。 本文中使用微分幾何形狀重構算法是基于廣泛使用的Frenet-Serret框架，通過求解Frenet公式中切向量、法向量和副法向量來獲得曲線的空間坐標。基于Franet-Serret框架的形狀重構算法的誤差傳播過程如下：應變測量誤差Δε導致曲率誤差Δκ和撓率誤差Δτ，這進一步導致切線向量ΔT的計算偏差。

ΔT在形狀長度s積分過程中不斷累積，最終導致歐幾里得距離重構誤差ΔE。 通過構建曲率誤差、撓率誤差與應變誤差關系，得到了任意空間曲線下距離重構誤差ΔE模型：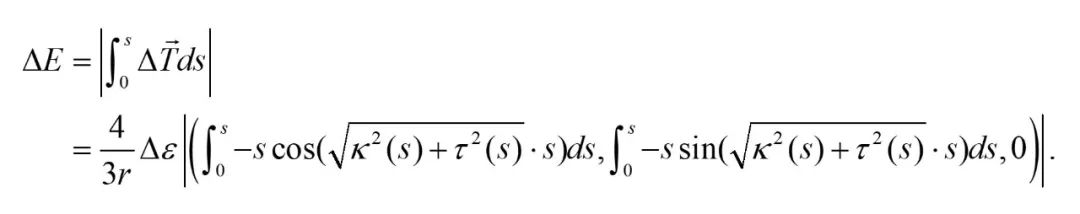

?

3.2 已定應變誤差下的重構誤差模型驗證

為了驗證重構誤差模型的有效性，我們進行了基于OFDR的多芯光纖形狀傳感實驗。我們把實驗分成兩部分。在第一部分，我們通過變量控制方法驗證了重構誤差與模型參數之間的關系。在第二部分，我們通過校準OFDR系統的最大應變誤差來驗證該模型對隨機應變誤差的相同適用性。

為了消除空間分辨率對實驗的影響，基于OFDR系統的SNR，將所有實驗的空間分辨率設置為最小3.6mm。如何選擇合理的形狀來驗證模型是一個關鍵點。形狀的復雜性無法定量定義。任何復雜的形狀都可以看作是由具有常數曲率κ和撓率τ的弧微段組成。

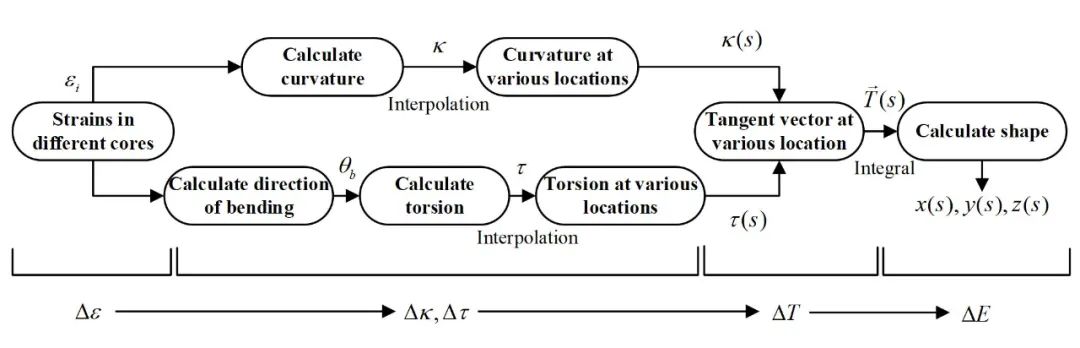
如果我們已經驗證了該模型對于具有恒定曲率和撓率的形狀是正確的，則該模型對于任何復雜形狀都是正確的。原因是復雜的形狀是許多簡單形狀的一個整體過程。為了將曲線的κ和τ控制在一個恒定值，我們結合3D打印技術設計并打印了一系列包含凹槽的模型，其中已知κ和τ曲線作為實驗中多芯光纖的形狀載體。

此外，我們選擇較短的光纖進行實驗，以使曲線的κ和τ的波動盡可能小。

首先驗證了撓率誤差與重構誤差關系，設計并制作了曲率為0.1m，撓率為0 rad/m, 2 rad/m, 4 rad/m, 6 rad/m, 8 rad/m 和 10 rad/m的3D打印模型如圖2所示。

實驗中多芯光纖纏繞在3D打印模型的凹槽里，形狀重構中加入5 με已定應變誤差，相關實驗結果如圖3（a）所示。

根據模型計算的重構誤差ΔE和實際測量的ΔE如圖3（b）所示。理論預測重構誤差與實驗結果相符。重構誤差隨著撓率增加而減小。

撓率較小時，重構誤差基本不隨撓率變化。當撓率較大時，重構誤差受撓率影響較大。

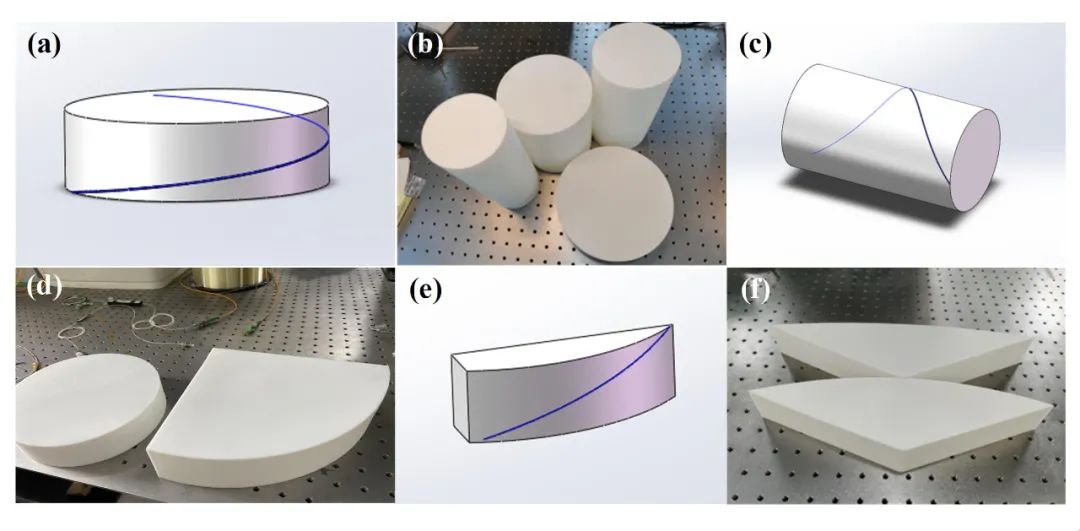
圖23D打印空間曲線模型 圖源：Optics Express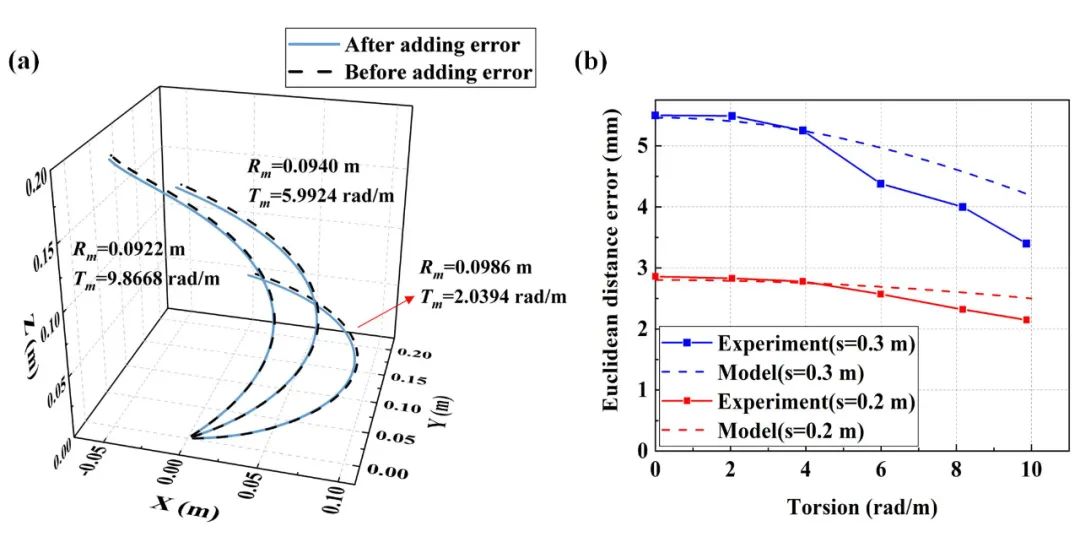



圖3撓率驗證結果（a）重構曲線（b）理論和實驗重構誤差對比

其次，驗證了曲率誤差與重構誤差關系。根據誤差模型和圖3（b）顯示關系，撓率為0時，重構誤差最大。這里采用二維曲線對重構誤差與曲率關系驗證，采用曲率半徑為0.05m，0.1m，0.2m, 0.35m, 0.5m和1m的3D打印模型如圖2所示。形狀重構中加入5με已定應變誤差。

二維曲線重構結果如圖4（a）所示。同時根據誤差模型計算了形狀長度為0.2m和0.3m下不同曲率半徑下的重構誤差并與測量值進行比較如圖4（b）所示。理論預測重構誤差與實驗結果相符。從圖4（b）可以看出，但曲率半徑較小時，重構誤差隨曲率半徑增大迅速增加。當曲率半徑較大時，重構誤差隨曲率半徑增大趨于穩定。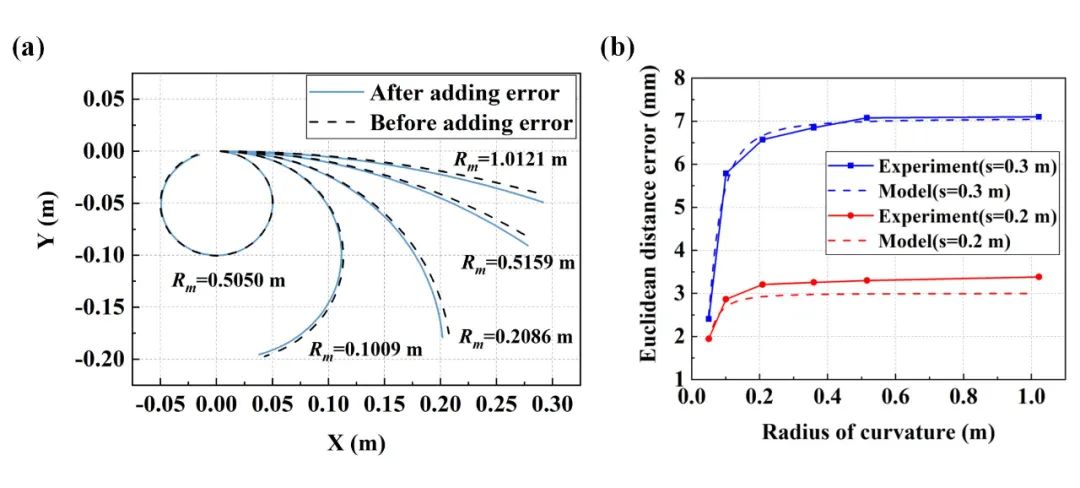



圖4 曲率驗證結果（a）重構曲線（b）理論和實驗重構誤差對比

再次，驗證了光纖長度與重構誤差關系。為了驗證這一關系，我們重構了一個螺旋線形狀，其長度為0.55m，曲率半徑為0.052m，撓率為3.8rad/m。形狀重構中加入5 με已定應變誤差。

螺旋線重構結果如圖5（a）所示。不同光纖長度下的重構誤差并與測量值進行比較如圖5（b）所示。理論預測重構誤差與實驗結果呈現高度一致性。重構誤差與光纖長度呈現非線性增加，其原因是光纖重構過程中誤差累積的結果。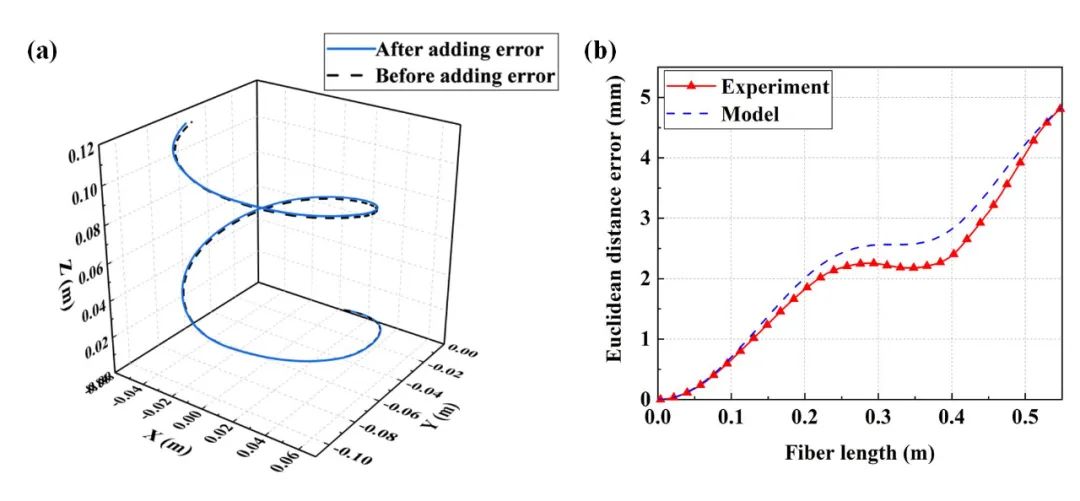



圖5 光纖長度與重構誤差驗證結果（a）重構曲線（b）理論和實驗重構誤差對比

最后，驗證重構誤差與應變測量誤差關系。采用0.3 m長曲率半徑為1m的弧形作為驗證模型。沿光纖長度上分別加入已定應變誤差f1 με, 2 με, 3 με, 4 με和5 με。

不同應變誤差下的測量和理論的重構誤差如圖6所示。理論預測重構誤差與實驗結果呈現高度一致性。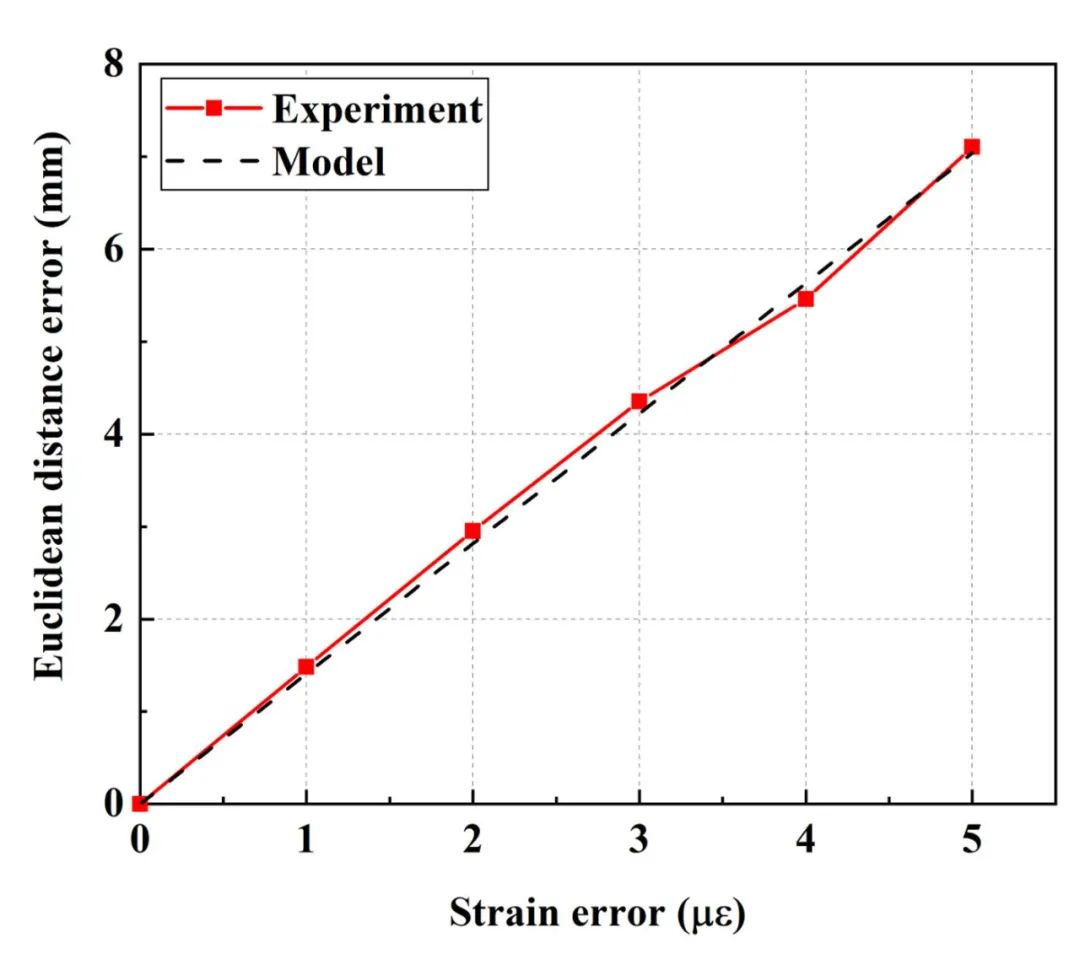



圖6 不同應變誤差下重構誤差驗證結果 圖源：Optics Express

3.3 隨機應變誤差下的重構誤差模型驗證

之前已經證明了已定應變誤差下誤差模型的可行性，但在實際應用中，OFDR沿光纖應變誤差是隨機的，而在OFDR應變傳感系統中會給出最大應變誤差Δεmax。本節中，我們將通過校準實驗中OFDR系統的Δεmax，進一步驗證重構誤差模型對隨機應變測量誤差的適用性。

如何構建不同Δεmax是實驗關鍵，我們這里采用設置不同應變測量分辨率通過與納米位移臺應變標定值比對，得到不同的Δεmax。應變校準范圍為0至25με，每5με進行一次校準。每個應變取80個應變測量點，并計算Δεmax。我們進行了形狀重構實驗，以驗證在不同Δεmax下重構誤差模型的適用性，其中測試形狀為曲率半徑為1m的二維圓弧。

在Δεmax分別為6.19με、6.22με、8.41με和10.04με的條件下進行形狀重構，并通過將重構曲線與標準曲線進行比較來計算測量重構誤差。顯示了測量重構和光纖長度之間的關系，并與基于重構誤差模型的理論值進行了比較，如圖7所示。

應該注意的是，圖7中觀察到的理論值和實測值之間的差異相對較大。然而，多次實驗的測量值沒有超過重構誤差模型計算的理論最大值。

由于OFDR系統的應變測量精度可以預先評估，因此根據Δεmax利用誤差模型得到重構誤差可以指導我們在光纖形狀傳感的設計中選擇合適的OFDR系統應變測量精度，并預測形狀重構精度。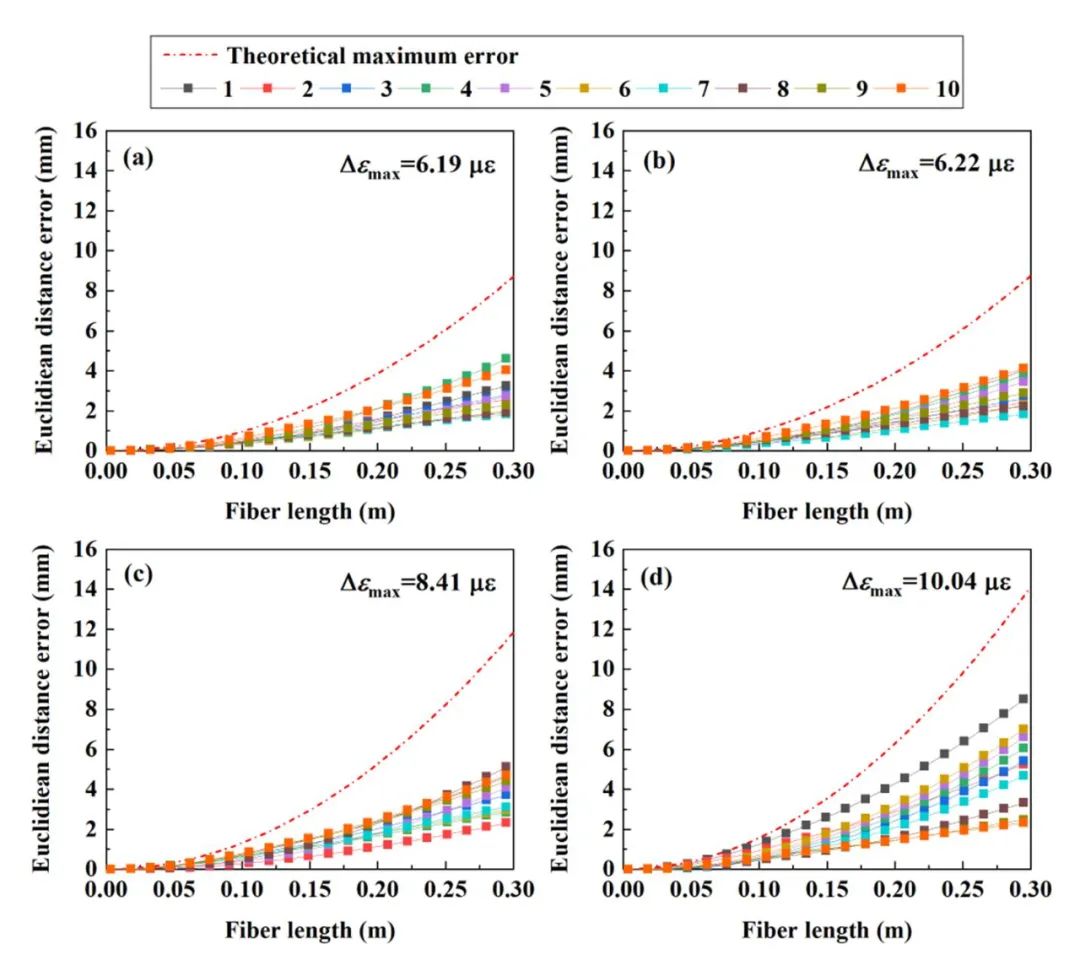



圖7 不同最大應變誤差下重構誤差驗證結果。(a) Δεmax=6.19 με. (b) Δεmax=6.22 με. (c) Δεmax=8.41 με. (d) Δεmax=10.04 με.

04應用與展望

三維形狀傳感誤差模型的建立不僅讓我們更清楚地了解了影響形狀重構結果的因素，還為光纖形狀傳感系統在不同應用場景下的設計和性能評估提供了理論指導。

當形狀測量精度要求以及待重構形狀的曲率和撓率范圍已明確時，所提出的重構誤差模型可用于計算滿足要求的最小應變測量誤差。

因此，該誤差模型可以有效地指導設計者為形狀傳感器的選擇合適的應變測量系統。

審核編輯：劉清