摘要

在機械臂抓取和操縱 3D 可變形物體時，必須考慮手指與物體之間的物理接觸約束，以驗證任務的穩定性。然而，以前的工作很少建立基于這些約束的接觸相互作用模型，從而能夠在抓取過程中精確控制力和變形。 本文考慮了可變形物體抓取過程的所有步驟，以通過計算初始接觸點（預抓取策略）以及隨后手指閉合時接觸區域的接觸力和局部變形來實現完整的抓取規劃。可變形物體的行為使用非線性各向同性質量彈簧系統建模，該系統能夠產生潛在變形。通過在仿真過程中結合兩種模型（接觸相互作用和物體變形），提出了一種新的抓取規劃方法，以保證3D抓取可變形物體的穩定性。最后，用 Barrett 手（3 指）和 6-DOF 工業機械臂執行幾個 3D 可變形物體的抓取實驗。不僅會獲得手+目標系統的最終穩定抓取策略，還會計算手臂+手接近策略（預抓取策略）。

1、規劃抓取方法簡介

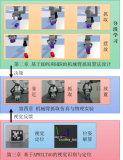
通過使用之前開發的接觸模型，我們可以處理高度可變形的物體，并精確估計變形時產生的接觸力。這些精確的估計將通過考慮新的抓握指標和優化機械手圍繞物體的預抓握策略來保證物體的靜態平衡。 圖 1 中的流程圖顯示了計算和執行穩健抓取（即手指在物體表面的策略）所需的所有步驟，通過我們的抓取規劃框架保證了物體的穩定性。

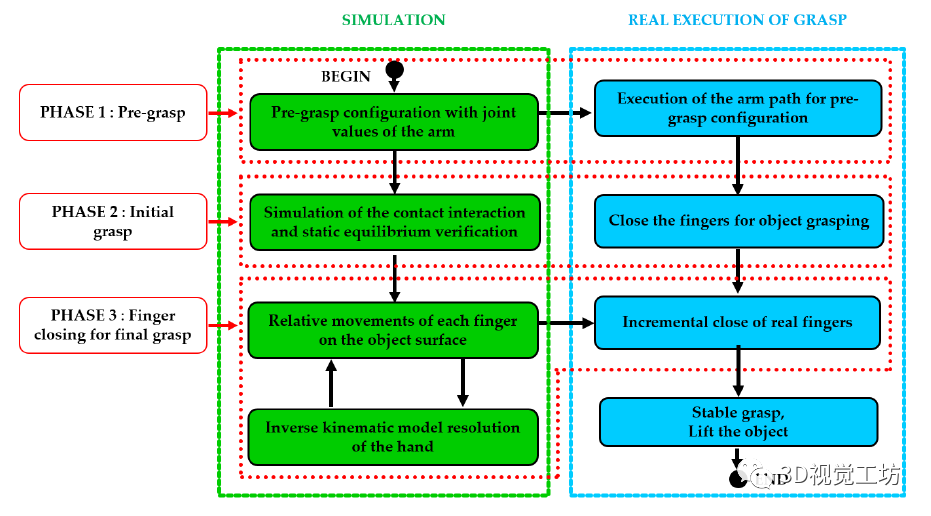
為了執行抓取計算，第一步確定預抓取策略。事實上，完整的抓取規劃策略分為兩個階段：首先，確定機械臂的策略，使手靠近物體，手指可以到達物體表面。然后，根據新的幾何標準確定手指的適當初始位姿以抓住物體。用于執行兩個階段的手臂和手的關節參數的確定通過其逆運動學 (IK) 的分辨率來保證。 一旦執行了預抓取，機器人就會移動到物體旁邊，手指達到初始抓握位置。當手指接觸到物體時，應該不會產生明顯的變形，因為首先會施加一個很小的接觸力，以避免抓握位置發生變化。一旦這個初始抓握被精確執行，算法的第三步就會被激活，手指的迭代閉合開始，基于接觸交互模型的模擬。在模擬的每次迭代中，都會更新目標的形變并計算生成的接觸力。計算出的接觸力用于評估物體 + 手指系統的靜態平衡。在仿真中重復迭代過程，直到達到靜態平衡（參見圖 1 中流程圖左側的仿真中的所有這些步驟）。 仿真過程完成后，可以通過執行從仿真中獲得的接觸力來執行對象的實際處理和操作（參見流程圖右側的步驟）。首先，將對象安裝在機器人的工作區，其相對配置與仿真開始時相同。然后，機械臂向預抓位置（即現實中的第 1 階段）移動，手指通過位置控制（即現實中的第 2 階段）移向初始接觸點。在此階段（實際上是階段 3 的開始），手指通過力控制閉合并逐漸擠壓物體，直到接觸力（由安裝在 Barrett 手的每個手指內的接觸傳感器測量）等于在模擬步驟中計算的接觸力。這些接觸力保證了物體-手系統的平衡（通過模擬驗證）。因此，物體可以從桌子上抬起沒有任何滑動的風險，可以穩健地操縱。在接下來的部分中，將詳細描述這些步驟，并通過對可變形物體進行真實的取放實驗進行驗證。

2、初始抓取策略

在本節中，我們將討論三指抓取物體穩定性的特征。這意味著根據從表示對象外部 3D 表面的所有點集中選擇的三個接觸點來確定力閉合策略。此過程中考慮了以下假設： 1）使用三個手指進行抓取操作，建模為半徑為 R 的半球 2）手指與物體的第一次接觸是點接觸 3）物體的外表面由一組點 表示，這些點由相對于物體質心 ( ) 的參考系測量的位置矢量 描述 事實上，當三指抓握收斂于理想的等邊抓握時，在穩定性、防滑性和力平衡方面更可靠。因此，每個三指抓握都可以用一個值來表征，該值表示它與等邊三角形的相似性。我們建議一種基于幾何標準的算法來找到這種等邊抓取。該算法首先通過掃描屬于接觸面 的點來確定所有可能的抓取三角形的集合。然后，使用Q1標準，把這些三角形的角度值（alpha、beta 和 lambda) 和（即，等邊三角形的角度）進行比較，以便選擇最接近等邊三角形的部分：

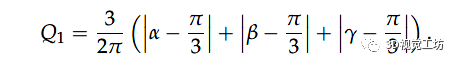
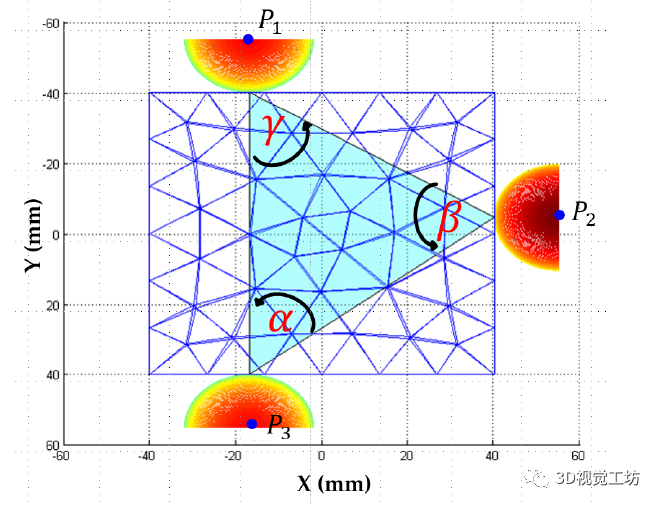
為了評估三角形的角度，我們使用由區間 [0, 0.3] 定義的誤差范圍。根據接觸面 的點密度，該算法可以給出幾種抓取配置。最后，使用第二個標準，稱為 Q2，以便在它們之間選擇一個。它測量物體 的質心與抓取三角形的中心 之間的距離，定義為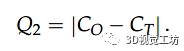

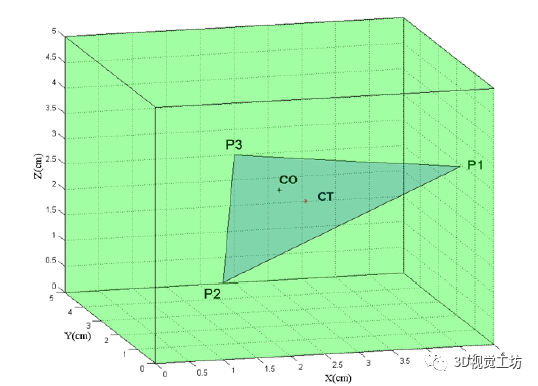
制定該標準是為了獲得相對于重力和慣性力產生的扭矩的穩定抓握。基于這兩個標準 Q1 和 Q2 的完整掌握合成算法在圖表“算法 1”中表示：

3、機械手的預抓策略：手指的放置

三指機械手的預抓取策略包括兩個步驟：第一步將手的方向與計算的初始抓取三角形對齊；第二步通過考慮手的運動學約束來調整對抓握的初始估計。第一步包括調整手的方向，使 TCP（工具中心點，沿垂直于手掌的軸定義）與 抓取三角形中心 重合。第二步涉及手指 IK 的分辨率，以估計關節值以達到初始抓取三角形的三個抓取點（、和 ）。如果未找到 IK ，則更改 TCP 線的長度并重新計算 IK 分辨率。當找到 IK 時，通過應用的逆表達式計算電機命令 以關注這些關節值。實現的算法如圖“算法 2”所示。在此迭代解決方案搜索的上下文中，我們認為該解決方案針對小于 2 度的每個手指的關節角度差值進行了驗證。

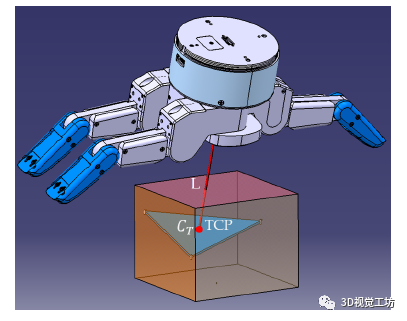
4、手 + 手臂系統的預抓策略：通過手臂實現軌跡移動

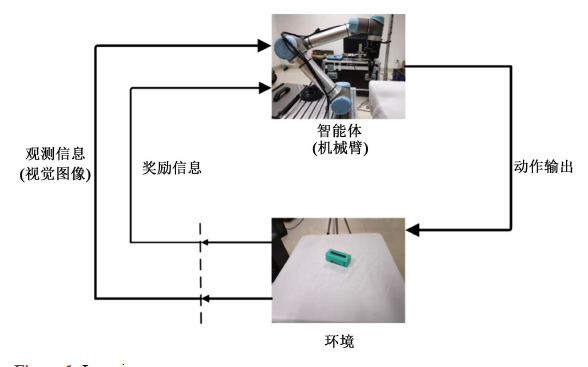
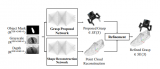
在建立手指的初始抓握點和手圍繞物體的相應預抓握策略之后，我們應該通過用攜帶它的機械臂移動手來執行與抓取。下圖顯示了手 + 手臂系統的預抓策略流程圖，該系統使用手臂和手的 IK 來實現初始抓握。為了實施這一規劃策略，我們選擇了一個 6 自由度機械臂（例如，用于我們真實實驗的 Viper S1700D），以便手可以在物體周圍的空間中獲得任何姿勢（位置 + 方向）。最初，目標放在桌子上，由平行于手臂底座的 XY 平面建模。

5、基于接觸交互建模的穩定抓取

為了能夠在手指閉合時評估實驗中發生的所有力的平衡，需要一個指尖和物體接觸的相互作用模型來精確確定抓取過程中力-形變間的關系。該模型將在沒有任何形變的情況下接收物體的初始抓握作為輸入。 在初步抓握之后，手指應反復靠近物體的中心，直到物體上的所有力達到平衡并執行穩定的抓握。為了計算這種平衡所需的指尖力，這種接觸模型的模擬是通過幾個連續的步驟來實現的。首先，檢測手指與物體之間的接觸；然后，計算接觸力（通過評估手指和物體之間的相對速度）。最后，檢查靜態平衡以確保抓握穩定性。在模擬的每次迭代中，動態模型都會更新由于施加的力而導致的整體形狀和接觸區域變形。為每個接觸點單獨計算接觸力，從而給出接觸區域中接觸壓力的真實分布。接觸模型考慮了法向力和摩擦引起的切向力的兩種模式：滑動和粘附模式。由于對象由一組非線性彈簧 - 阻尼器對建模，因此非線性法向力由下式給出：

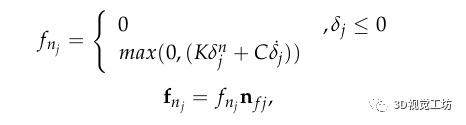
其中 是沿接觸面 的法線方向測量的穿透距離； 和 分別是接觸剛度和阻尼常數。 需要對沿每個觸點作用的切向力進行建模，以防止任何滑動并確保抓握穩定性。接觸模型考慮了摩擦引起的切向力的兩種模式：滑動和粘附模式。在這個模型中，平行彈簧阻尼器的一端通過滑塊元件連接到地面，另一端連接到指尖。因此，接觸點位置在滑動條件下動態變化。這些變量分別對應于接觸點處由于粘附和滑動引起的相對位移。如果接觸斷開，它們會動態重置為零。滑動摩擦力可以根據庫侖定律定義如下：

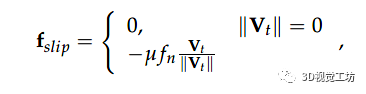
其中 、 和 分別是摩擦系數、法向力和切向速度。使用該模型，接觸點位置在滑動條件下動態變化。如果切向力范數小于滑動閾值，則我們有一個粘附函數，其切向力定義為

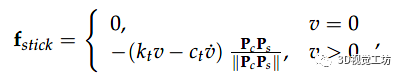
其中 是接觸面上的切向變形， 是接觸點位置， 是粘附狀態下的接觸點位置。參數 和 分別是使用 Dopico 方法估計的切向剛度和阻尼系數。 如本節開頭所述，此接觸模型將在達到初始抓取位置（作為預抓取策略的輸出獲得）并且手指開始接觸物體表面后執行。事實上，在 Matlab 中實現了抓取執行策略的模擬，以確定應該施加的接觸力以實現穩定抓取。該模擬將迭代地將手指靠近物體的中心，通過求解接觸模型來評估傳遞給物體的力，更新由于變形導致的接觸表面的狀態，并驗證手 + 物體系統的靜態平衡。當在模擬中獲得這種靜態平衡時，模擬手指施加的接觸力將作為真實機械手力控制的參考。

總結

本文致力于用工業機械手（機械手+機械臂）進行可變形物體抓取規劃的完整過程。首先，這需要定義物體表面上的抓取點，從而確定初始抓取策略。然后，提出了通過考慮手臂和手的運動學約束。因此，抓取規劃分為兩個階段，第一階段，確定機器人手臂的策略，使手靠近物體；確定手指的適當策略以抓住物體， 手臂和手的關節參數的確定是由它們的逆運動學的分辨率來保證的。只考慮到手的情況下，實施的策略包括首先將 TCP（垂直于手掌的線）置于與抓握三角形中心（在初始抓握合成中獲得）的交點處，并將其與法線對齊 這個抓取三角形的矢量。第二步是迭代搜索三個手指的關節參數的解決方案，以便使它們與先前由力閉合型穩定性條件定義的抓取點相對應。因此，該最終抓取方案通過應用所提出的預抓取策略，將基于力閉合的一般幾何標準（即，它僅考慮物體的形狀）的初始抓取與機械手的運動學約束相結合。然而，這種抓握策略確實只保證了剛性物體抓握的穩健性，而不能保證可變形物體的抓握穩健性。因此，當手指接觸到要抓握的可變形物體時，就會激活力-形變方案。該方案基于物體與手指相互作用的模擬，它獲得了手指應施加的接觸力閾值，以確保在使物體表面變形時穩定抓握物體。最后，執行真實手指的迭代閉合以獲得與真實物體的接觸力。

審核編輯 ：李倩