使用史密斯圖進(jìn)行射頻阻抗匹配的教程。示例顯示了繪制反射系數(shù)、阻抗和導(dǎo)納的示例。MAX2472的樣本匹配網(wǎng)絡(luò)采用圖形方法設(shè)計(jì)為900MHz。
經(jīng)過驗(yàn)證,史密斯圖仍然是確定傳輸線阻抗的基本工具。
在處理RF應(yīng)用的實(shí)際實(shí)現(xiàn)時,總有一些噩夢般的任務(wù)。一是需要匹配互連塊的不同阻抗。通常包括天線到低噪聲放大器 (LNA)、功率放大器輸出 (RFOUT) 到天線以及 LNA/VCO 輸出到混頻器輸入。匹配任務(wù)是將信號和能量從“源”正確傳輸?shù)健柏?fù)載”所必需的。
在高射頻下,雜散元件(如導(dǎo)線電感、層間電容和導(dǎo)體電阻)對匹配網(wǎng)絡(luò)具有重大但不可預(yù)測的影響。在幾十兆赫茲以上,理論計(jì)算和模擬往往是不夠的。在確定適當(dāng)?shù)淖罱K值時,必須考慮原位射頻實(shí)驗(yàn)室測量以及調(diào)諧工作。需要計(jì)算值來設(shè)置結(jié)構(gòu)類型和目標(biāo)組件值。
有許多方法可以進(jìn)行阻抗匹配,包括:
計(jì)算機(jī)模擬:復(fù)雜但易于使用,因?yàn)榇祟惸M器專用于不同的設(shè)計(jì)功能,而不是阻抗匹配。設(shè)計(jì)人員必須熟悉需要輸入的多個數(shù)據(jù)輸入和正確的格式。他們還需要專業(yè)知識,以便在大量結(jié)果中找到有用的數(shù)據(jù)。此外,電路仿真軟件不會預(yù)先安裝在計(jì)算機(jī)上,除非它們專用于此類應(yīng)用程序。
手動計(jì)算:由于方程的長度(“公里”)和要操作的數(shù)字的復(fù)雜性,因此很乏味。
本能:只有在一個人在射頻行業(yè)投入多年后才能獲得。簡而言之,這是給超級專家的。
史密斯圖: 本文集中討論的內(nèi)容。
本文的主要目的是回顧史密斯圖的結(jié)構(gòu)和背景,并總結(jié)其使用的實(shí)際方法。討論的主題包括參數(shù)的實(shí)際說明,例如查找匹配的網(wǎng)絡(luò)組件值。當(dāng)然,匹配最大功率傳輸并不是我們唯一可以用史密斯圖做的事情。它們還可以幫助設(shè)計(jì)人員完成優(yōu)化最佳噪聲系數(shù)、確保品質(zhì)因素影響和評估穩(wěn)定性分析等任務(wù)。
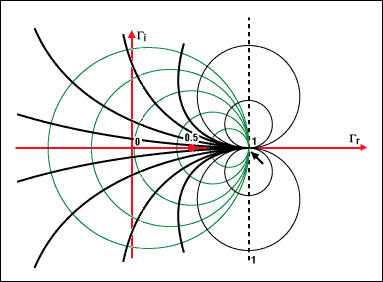
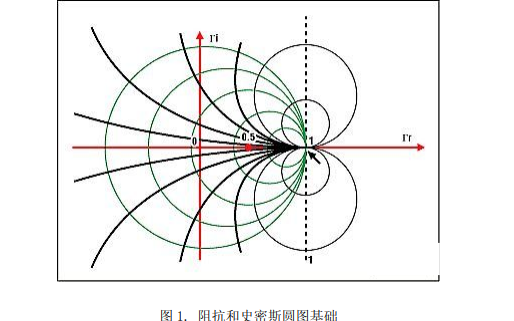
圖1.阻抗和史密斯圖的基本原理。
快速入門
在介紹史密斯圖實(shí)用程序之前,謹(jǐn)慎的做法是簡要回顧一下RF條件下(100MHz以上)IC布線的波傳播現(xiàn)象。這對于意外情況可能有效,例如RS-485線路、PA和天線之間、LNA和下變頻器/混頻器之間等。
眾所周知,為了獲得從電源到負(fù)載的最大功率傳輸,源阻抗必須等于負(fù)載阻抗的復(fù)共軛,或者:
RS+ jXS= RL- jXL
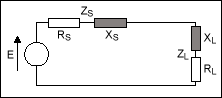
圖2.R 的示意圖S+ jXS= RL- jXL.
在這種情況下,從電源到負(fù)載的能量最大化。此外,為了進(jìn)行有效的電力傳輸,需要此條件以避免能量從負(fù)載反射回電源。對于視頻線、射頻和微波網(wǎng)絡(luò)等高頻環(huán)境尤其如此。
它是什么
史密斯圖是一個圓形圖,上面有很多交錯的圓圈。如果使用得當(dāng),無需任何計(jì)算即可匹配具有明顯復(fù)雜結(jié)構(gòu)的阻抗。唯一需要的努力是沿圓圈讀取和跟蹤值。
史密斯圖是復(fù)反射系數(shù)(也稱為伽馬,用Γ符號化)的極坐標(biāo)圖。或者,它在數(shù)學(xué)上定義為 1 端口散射參數(shù) s 或 s11.
史密斯圖是通過檢查阻抗必須匹配的負(fù)載來開發(fā)的。您不是直接考慮其阻抗,而是表示其反射系數(shù)ΓL,用于表征負(fù)載(如導(dǎo)納、增益和跨導(dǎo))。The ΓL在處理射頻頻率時更有用。
我們知道反射系數(shù)定義為反射電壓波和入射電壓波之間的比率:
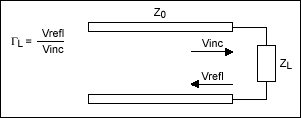
圖3.負(fù)載阻抗。
來自負(fù)載的反射信號量取決于源阻抗和負(fù)載阻抗之間的不匹配程度。其表達(dá)式定義如下:

因?yàn)樽杩故菑?fù)數(shù),所以反射系數(shù)也是一個復(fù)數(shù)。
為了減少未知參數(shù)的數(shù)量,凍結(jié)應(yīng)用程序中經(jīng)常出現(xiàn)且常見的參數(shù)很有用。這里 Z0(特性阻抗)通常是一個常數(shù)和實(shí)際的工業(yè)歸一化值,例如50Ω、75Ω、100Ω和600Ω。然后,我們可以通過以下方式定義歸一化負(fù)載阻抗:

通過這種簡化,我們可以將反射系數(shù)公式重寫為:
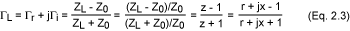
在這里,我們可以看到負(fù)載阻抗與其反射系數(shù)之間的直接關(guān)系。不幸的是,關(guān)系的復(fù)雜性在實(shí)際中沒有用,因此我們可以將史密斯圖用作上述方程的一種圖形表示。
要構(gòu)建圖表,必須重寫方程以提取標(biāo)準(zhǔn)幾何圖形(如圓或雜散線)。
首先,將等式 2.3 反轉(zhuǎn),得到:

和

通過將等式 2.5 的實(shí)部和虛部相等,我們得到了兩個獨(dú)立的新關(guān)系:

然后,通過將方程2.6至2.8發(fā)展為最終方程2.13來操縱等式2.14。該方程是以坐標(biāo) [r/(r + 1), 0] 為中心且半徑為 1/(1 + r) 的圓的復(fù)平面 (Γr, Γi) 中的參數(shù)方程 (x - a)2 + (y - b)2 = R2 形式的關(guān)系。
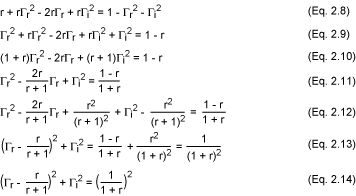
有關(guān)更多詳細(xì)信息,請參見圖 4a。
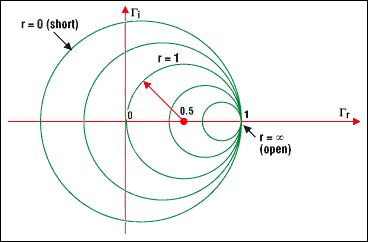
圖 4a.位于圓上的點(diǎn)是所有阻抗,其特征是相同的實(shí)際阻抗部分值。例如,圓 r = 1 以坐標(biāo) (0.5, 0) 為中心,半徑為 0.5。它包括點(diǎn)(0,0),這是反射零點(diǎn)(負(fù)載與特性阻抗匹配)。短路作為負(fù)載,呈現(xiàn)一個以坐標(biāo) (0, 0) 為中心的圓,半徑為 1。對于開路負(fù)載,圓退化為單個點(diǎn)(以 1, 0 為中心,半徑為 0)。這對應(yīng)于最大反射系數(shù) 1,此時整個入射波被完全反射。
在開發(fā)史密斯圖時,應(yīng)注意某些預(yù)防措施。這些是最重要的:
所有圓在坐標(biāo) (1, 0) 處都有一個相同的唯一相交點(diǎn)。
沒有阻力 (r = 0) 的零Ω圓是最大的一個。
無限電阻圓在(1, 0)處減小到一個點(diǎn)。
不應(yīng)該有負(fù)阻力。如果發(fā)生一個(或多個),我們將面臨振蕩條件的可能性。
只需選擇與新值相對應(yīng)的另一個圓圈即可選擇另一個電阻值。
從頭再來
繼續(xù),我們使用等式 2.15 到 2.18 將等式 2.7 進(jìn)一步發(fā)展為另一個參數(shù)方程。這導(dǎo)致等式2.19。
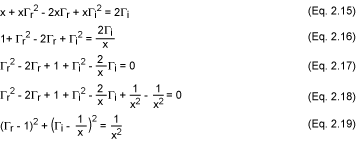
同樣,2.19 是以坐標(biāo) (1, 1/x) 為中心且半徑為 1/x 的圓的復(fù)平面 (Γr, Γi) 中類型 (x - a)2 + (y - b)2 = R2 的參數(shù)方程。
有關(guān)更多詳細(xì)信息,請參見圖 4b。
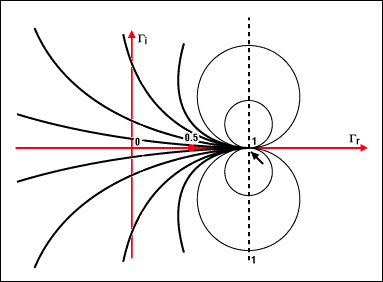
圖 4b.位于圓上的點(diǎn)是所有由相同的假想阻抗部分值x表征的阻抗。例如,圓 × = 1 以坐標(biāo) (1, 1) 為中心,半徑為 1。所有圓(常量 x)都包含點(diǎn) (1, 0)。與實(shí)部圓不同,×可以是正數(shù),也可以是負(fù)數(shù)。這解釋了復(fù)平面底部的重復(fù)鏡像圓。所有圓心都放置在垂直軸上,與點(diǎn) 1 相交。
明白了嗎?
為了完成我們的史密斯圖,我們疊加了兩個圓圈的族。然后可以看出,一個家庭的所有圓圈將與另一個家庭的所有圓圈相交。知道阻抗,以r+jx的形式,可以確定相應(yīng)的反射系數(shù)。只需要找到對應(yīng)于值 r 和 x 的兩個圓的交點(diǎn)。
這也是互惠
反向操作也是可能的。知道反射系數(shù),找到在該點(diǎn)相交的兩個圓,并在圓上讀取相應(yīng)的值 r 和 ×。此過程如下:
確定阻抗作為史密斯圖上的一個點(diǎn)。
找到阻抗的反射系數(shù) (Γ)。
具有特性阻抗和Γ,找到阻抗。
將阻抗轉(zhuǎn)換為導(dǎo)納。
找到等效阻抗。
找到所需反射系數(shù)的分量值(特別是匹配網(wǎng)絡(luò)的元素,請參見圖 7)。
要推斷
由于史密斯圖解析技術(shù)基本上是一種圖形方法,因此解決方案的精度直接取決于圖形定義。下面是一個可以用史密斯圖表示的射頻應(yīng)用示例:
例:考慮50Ω端接的特性阻抗和以下阻抗:
| Z1= 100 + j50Ω | Z2= 75 - j100Ω | Z3= j200Ω | Z4= 150Ω |
| Z5= ∞ (開路) | Z6= 0(短路) | Z7= 50Ω | Z8= 184 - j900Ω |
然后,歸一化并繪制圖(參見圖 5)。這些點(diǎn)的繪制方式如下:
| z1= 2 + j | z2= 1.5 - j2 | z3= j4 | z4= 3 |
| z5= 8 | z6= 0 | z7= 1 | z8= 3.68 - j18 |
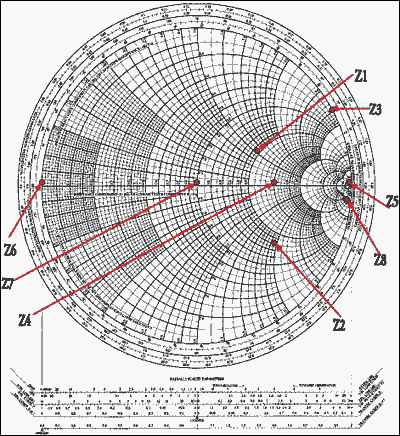
對于更大的圖像 (PDF)
圖5.在史密斯圖表上繪制的點(diǎn)。
現(xiàn)在可以直接提取圖5的史密斯圖上的反射系數(shù)Γ。繪制阻抗點(diǎn)(恒定電阻圓和恒定電抗圓的交點(diǎn))后,只需讀取水平軸和垂直軸上的矩形坐標(biāo)投影即可。這將得到反射系數(shù)的實(shí)部Γr和反射系數(shù)的虛部Γi(見圖6)。
也可以采用示例中介紹的八個案例,并直接從圖 6 的史密斯圖中提取其相應(yīng)的Γ。這些數(shù)字是:
| Γ1= 0.4 + 0.2j | Γ2= 0.51 - 0.4j | Γ3= 0.875 + 0.48j | Γ4= 0.5 |
| Γ5= 1 | Γ6= -1 | Γ7= 0 | Γ8= 0.96 - 0.1j |
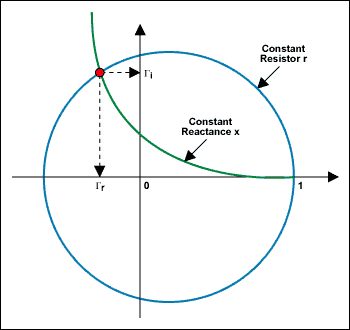
圖6.沿 X-Y 軸直接提取反射系數(shù)Γ實(shí)數(shù)和虛部。
使用準(zhǔn)入
史密斯圖是通過考慮阻抗(電阻和電抗)來構(gòu)建的。一旦建立了史密斯圖,它就可以用于分析串聯(lián)和平行世界中的這些參數(shù)。在系列中添加元素非常簡單。可以添加新元素,并通過簡單地沿著圓移動到其各自的值來確定其效果。但是,并行對元素求和是另一回事。這需要考慮其他參數(shù)。通常,在導(dǎo)納世界中使用并行元素更容易。
我們知道,根據(jù)定義,Y = 1/Z 和 Z = 1/Y。準(zhǔn)入以 mhos 或 Ω 表示-1,雖然現(xiàn)在表示為西門子或 S。而且,由于 Z 是復(fù)雜的,因此 Y 也必須是復(fù)雜的。
因此,Y = G + jB (2.20),其中G稱為“電導(dǎo)”,B稱為元素的“敏感性”。不過,謹(jǐn)慎行事很重要。通過遵循邏輯假設(shè),我們可以得出結(jié)論,G = 1/R 和 B = 1/X。然而,情況并非如此。如果使用此假設(shè),則結(jié)果將不正確。
使用導(dǎo)納時,我們必須做的第一件事是歸一化 y = Y/Y0.這導(dǎo)致 y = g + jb。那么,反射系數(shù)會發(fā)生什么變化呢?通過以下工作:
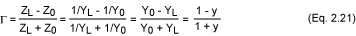
事實(shí)證明,G 的表達(dá)式與 z 相反,Γ(y) = -Γ(z)。
如果我們知道 z,我們可以反轉(zhuǎn)Γ的符號并找到一個距離 (0, 0) 相同距離但方向相反的點(diǎn)。通過圍繞中心點(diǎn)旋轉(zhuǎn) 180° 角度可以獲得相同的結(jié)果(見圖 7)。
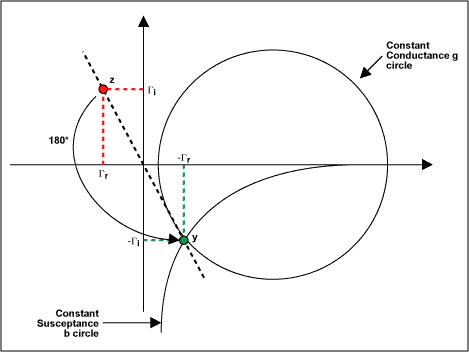
圖7.180°旋轉(zhuǎn)的結(jié)果。
當(dāng)然,雖然 Z 和 1/Y 確實(shí)表示相同的分量,但新點(diǎn)顯示為不同的阻抗(新值在史密斯圖中具有不同的點(diǎn)和不同的反射值,依此類推)。發(fā)生這種情況是因?yàn)樵搱D是阻抗圖。但新的一點(diǎn),實(shí)際上是一種承認(rèn)。因此,圖表上讀取的值必須讀取為西門子。
雖然這種方法足以進(jìn)行轉(zhuǎn)換,但在并行處理元件時,它不適用于確定電路分辨率。
導(dǎo)納史密斯圖
在前面的討論中,我們看到阻抗史密斯圖上的每個點(diǎn)都可以通過圍繞Γ復(fù)平面的原點(diǎn)旋轉(zhuǎn) 180° 來轉(zhuǎn)換為其導(dǎo)納對應(yīng)物。因此,通過將整個阻抗史密斯控制圖旋轉(zhuǎn)180°可以獲得導(dǎo)納史密斯圖。這非常方便,因?yàn)樗藰?gòu)建另一個圖表的必要性。所有圓的交點(diǎn)(恒定電導(dǎo)和恒定置射)自動位于點(diǎn) (-1, 0)。有了這個情節(jié),并行添加元素也變得更加容易。在數(shù)學(xué)上,導(dǎo)納史密斯圖的構(gòu)造由以下公式創(chuàng)建:

然后,反轉(zhuǎn)等式:
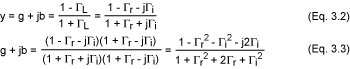
接下來,通過將等式 3.3 的實(shí)部和虛部相等,我們得到兩個新的獨(dú)立關(guān)系:

通過開發(fā)等式3.4,我們得到以下結(jié)果:
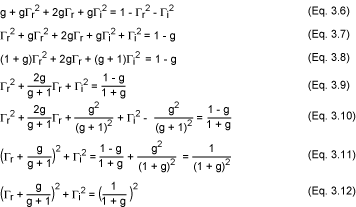
它又是圓的復(fù)平面 (Γr, Γi) 中類型 (x - a)2 + (y - b)2 = R2 (方程 3.12) 的參數(shù)方程,其坐標(biāo)以 [-g/(g + 1), 0] 為中心,半徑為 1/(1 + g)。
此外,通過開發(fā)等式3.5,我們表明:
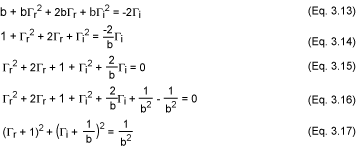
這又是類型 (x - a)2 + (y - b)2 = R2 的參數(shù)方程(方程 3.17)。
等效阻抗分辨率
在解決串聯(lián)和并聯(lián)元素混合在一起的問題時,我們可以使用相同的史密斯圖,并圍繞存在從 z 到 y 或 y 到 z 的轉(zhuǎn)換的任何點(diǎn)旋轉(zhuǎn)它。
讓我們考慮圖 8 的網(wǎng)絡(luò)(元素使用 Z 歸一化0= 50Ω).串聯(lián)電抗(x)對于電感為正,對于電容為負(fù)。磁化率(b)對電容為正,對電感為負(fù)。
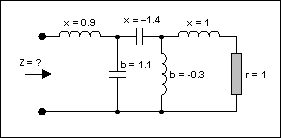
圖8.多元件電路。
電路需要簡化(見圖9)。從右側(cè)開始,那里有一個電阻器和一個值為1的電感,我們繪制一個系列點(diǎn),其中r圓= 1,l圓= 1。這成為A點(diǎn)。由于下一個元素是分流(平行)中的元素,我們切換到導(dǎo)納史密斯控制圖(通過將整個平面旋轉(zhuǎn) 180°)。但是,要做到這一點(diǎn),我們需要將前一點(diǎn)轉(zhuǎn)換為準(zhǔn)入。這變成了 A'。然后我們將平面旋轉(zhuǎn) 180°。我們現(xiàn)在處于準(zhǔn)入模式。分流元件可以通過沿電導(dǎo)圈移動對應(yīng)于0.3的距離來添加。這必須以逆時針方向(負(fù)值)完成,并給出點(diǎn) B。然后我們還有另一個系列元素。我們再次切換回阻抗史密斯圖。
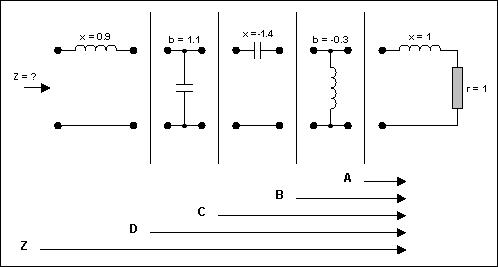
圖9.圖 8 的網(wǎng)絡(luò)及其元素進(jìn)行了細(xì)分分析。
在執(zhí)行此操作之前,再次有必要將前一點(diǎn)重新轉(zhuǎn)換為阻抗(這是導(dǎo)納)。轉(zhuǎn)換后,我們可以確定 B'。使用先前建立的例程,圖表再次旋轉(zhuǎn) 180° 以返回到阻抗模式。串聯(lián)元件是沿著電阻圈沿著對應(yīng)于1.4的距離和標(biāo)記點(diǎn)C相加的。這需要逆時針完成(負(fù)值)。對于下一個元素,將執(zhí)行相同的操作(轉(zhuǎn)換為導(dǎo)納和平面旋轉(zhuǎn))。然后沿恒定電導(dǎo)圈順時針方向移動規(guī)定的距離(1.1)(因?yàn)樵撝禐檎N覀儗⑵錁?biāo)記為 D。最后,我們重新轉(zhuǎn)換回阻抗模式并添加最后一個元件(串聯(lián)電感)。然后,我們確定位于電阻圓 0.2 和電抗圓 0.5 的交點(diǎn)處的所需值 z。因此,z 被確定為 0.2 + j0.5。如果系統(tǒng)特性阻抗為50Ω,則Z = 10 + j25Ω(見圖10)。
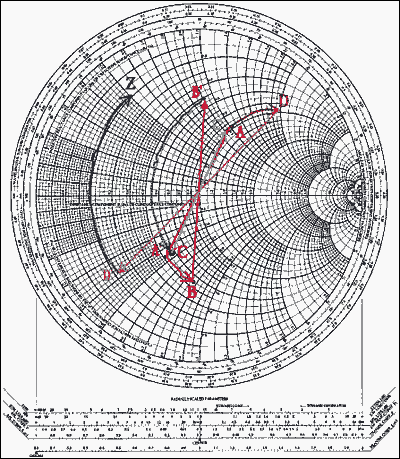
對于更大的圖像 (PDF)
圖 10.繪制在史密斯圖上的網(wǎng)絡(luò)元素。
按步驟匹配阻抗
史密斯圖的另一個功能是能夠確定阻抗匹配。這是查找給定網(wǎng)絡(luò)的等效阻抗的反向操作。此處,阻抗固定在兩個接入端(通常是源極和負(fù)載),如圖11所示。目標(biāo)是設(shè)計(jì)一個在它們之間插入的網(wǎng)絡(luò),以便進(jìn)行適當(dāng)?shù)淖杩蛊ヅ洹?/p>
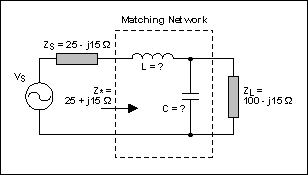
圖 11.具有已知阻抗和未知元件的代表電路。
乍一看,這似乎并不比找到等效阻抗更困難。但問題是,可以存在無限數(shù)量的匹配網(wǎng)絡(luò)組件組合,從而產(chǎn)生類似的結(jié)果。可能還需要考慮其他輸入(例如濾波器類型結(jié)構(gòu)、質(zhì)量因數(shù)和有限的組件選擇)。
為此選擇的方法需要在史密斯圖上添加串聯(lián)和分流元件,直到達(dá)到所需的阻抗。從圖形上看,它似乎找到了一種鏈接史密斯圖上的點(diǎn)的方法。同樣,說明該方法的最佳方法是以需求為例。
目標(biāo)是匹配源阻抗(ZS) 到負(fù)載 (Z)L)的工作頻率為60MHz(見圖11)。網(wǎng)絡(luò)結(jié)構(gòu)已固定為低通,L型(另一種方法是將問題視為如何強(qiáng)制負(fù)載顯示為值= Z的阻抗S,Z 的復(fù)共軛物S).以下是找到解決方案的方法。
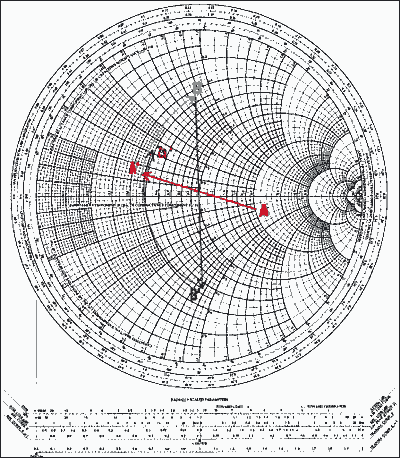
對于更大的圖像 (PDF)
圖 12.圖 11 的網(wǎng)絡(luò)及其點(diǎn)繪制在史密斯圖上。
首先要做的是規(guī)范化不同的阻抗值。如果未給出,請選擇與荷載/源值在相同范圍內(nèi)的值。假設(shè) Z0為50Ω。因此 zS= 0.5 - j0.3, z*S= 0.5 + j0.3,并且zL= 2 - j0.5。
接下來,在圖表上定位兩個點(diǎn)。標(biāo)記 A 表示 zL和 D 表示 z*S.
然后確定連接到負(fù)載的第一個元件(并聯(lián)中的電容器)并轉(zhuǎn)換為導(dǎo)納。這給了我們A'點(diǎn)。
確定電容器C連接后下一個點(diǎn)將出現(xiàn)的電弧部分。由于我們不知道C的值,因此我們不知道在哪里停止。然而,我們確實(shí)知道方向。分流中的 C 表示在導(dǎo)納史密斯控制圖上沿順時針方向移動,直到找到該值。這將是B點(diǎn)(準(zhǔn)入)。由于下一個元件是串聯(lián)元件,因此必須將B點(diǎn)轉(zhuǎn)換為阻抗平面。然后可以獲得B'點(diǎn)。B'點(diǎn)必須與D位于同一電阻圓上.圖形上,從A'到D只有一個解決方案,但中間點(diǎn)B(因此B')需要通過“測試和嘗試”設(shè)置進(jìn)行驗(yàn)證。找到點(diǎn) B 和 B' 后,我們可以測量弧 A' 到 B 和弧 B' 到 D 的長度。第一個給出 C 的歸一化置疑值。第二個給出L的歸一化電抗值。弧 A' 到 B 的測量值為 b = 0.78,因此 B = 0.78 × Y0= 0.0156S。因?yàn)棣谻 = B,那么C = B/ω = B/(2 π f) = 0.0156/[2π(60 × 106)] = 41.4pF。
弧 B' 到 D 的測量值為 x = 1.2,因此 X = 1.2 × Z0= 60Ω.因?yàn)?ωL = X,所以 L = X/ω = X/(2 π f) = 60/[2π(60 × 106)] = 159nH。
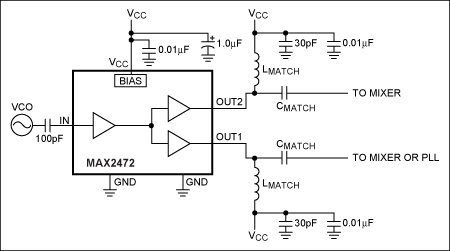
圖 13.MAX2472典型工作電路
第二個示例將MAX2472的輸出與50Ω負(fù)載阻抗(zL)的工作頻率為900MHz(見圖14)。該網(wǎng)絡(luò)將使用MAX2472數(shù)據(jù)資料中所示的相同配置。上圖顯示了具有并聯(lián)電感器和串聯(lián)電容器的匹配網(wǎng)絡(luò)。以下是找到解決方案的方法。
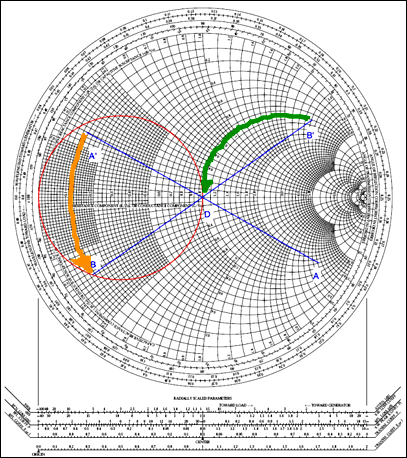
圖 14.圖 13 的網(wǎng)絡(luò)及其點(diǎn)繪制在史密斯圖上。
首先要做的是轉(zhuǎn)換 S22散射參數(shù)轉(zhuǎn)換為其等效歸一化源阻抗。MAX2472使用Z0為50Ω。因此 S22= 0.81/-29.4° 變?yōu)?zS= 1.4 - j3.2, zL= 1 和 zL* = 1。
接下來,在圖表上定位兩個點(diǎn)。標(biāo)記 A 表示 zS和 D 表示 zL*.由于連接到源的第一個元件是并聯(lián)電感,因此請將源阻抗轉(zhuǎn)換為導(dǎo)納。這給了我們A'點(diǎn)。
確定電感L連接后下一個點(diǎn)將出現(xiàn)的電弧部分火柴.因?yàn)槲覀儾恢繪的值火柴,我們不知道在哪里停下來。但是,我們確實(shí)知道,在添加 L 之后火柴(并轉(zhuǎn)換回阻抗),得到的源阻抗應(yīng)位于r = 1圓上。因此,附加串聯(lián)電容器C火柴可以使所得阻抗達(dá)到z = 1 + J0。通過將r = 1圓圍繞原點(diǎn)旋轉(zhuǎn)180°,我們繪制出與r = 1圓相對應(yīng)的所有可能的導(dǎo)納值。這個反射圓和與點(diǎn)A'一起使用的恒定電導(dǎo)圓的交點(diǎn)給了我們B點(diǎn)(導(dǎo)納)。B點(diǎn)對阻抗的反射成為B'點(diǎn)。
找到點(diǎn) B 和 B' 后,我們可以測量弧 A' 到 B 和弧 B' 到 D 的長度。第一次測量給出L的歸一化置化置化值火柴.第二個給出C的歸一化電抗值火柴.弧 A' 到 B 的測量值為 b = -0.575,因此 B = -0.575 × Y0= 0.0115S。因?yàn)?1/ωL = B,那么 L火柴= 1/Bω = 1/(B2πf) = 1/(0.01156 × 2 × π × 900 × 106) = 15.38nH,四舍五入為 15nH。弧 B' 到 D 的測量值為 × = -2.81,因此 X = -2.81 × Z0= -140.5Ω.因?yàn)?-1/ωC = X,那么C火柴= -1/Xω = -1/(X2πf) = -1/(-140.5 × 2 × π × 900 × 106) = 1.259pF,四舍五入為 1pF。雖然這些計(jì)算值未考慮元件的寄生電感和電容,但它們產(chǎn)生的值接近數(shù)據(jù)手冊規(guī)定的值L火柴= 12nH 和 C火柴= 1pF。
結(jié)論
鑒于當(dāng)今軟件的豐富性和高速高功率計(jì)算機(jī)的可訪問性,人們可能會質(zhì)疑是否需要這種基本和基本的方法來確定電路基本原理。
實(shí)際上,使工程師成為真正工程師的不僅是學(xué)術(shù)知識,還有使用各種資源解決問題的能力。將幾個數(shù)字插入程序并讓它吐出解決方案很容易。當(dāng)解決方案復(fù)雜且多方面時,擁有一臺計(jì)算機(jī)來完成繁重的工作特別方便。但是,了解已移植到計(jì)算機(jī)平臺的基本理論和原理以及它們的來源,使工程師或設(shè)計(jì)師成為更全面和自信的專業(yè)人士,并使結(jié)果更加可靠。
審核編輯:郭婷
-
放大器
+關(guān)注
關(guān)注
143文章
13631瀏覽量
214213 -
功率放大器
+關(guān)注
關(guān)注
102文章
3626瀏覽量
132294 -
RF
+關(guān)注
關(guān)注
65文章
3059瀏覽量
167364
發(fā)布評論請先 登錄
相關(guān)推薦
阻抗匹配與史密斯原圖:基本原理
阻抗匹配與史密斯(Smith)圓圖:基本原理
阻抗匹配與史密斯(Smith)圓圖
阻抗匹配與史密斯圓圖
怎樣理解阻抗匹配_pcb阻抗匹配如何計(jì)算

阻抗匹配是什么意思_阻抗匹配原理詳解
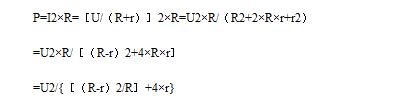
史密斯圓圖的的天線阻抗匹配解決方案

阻抗匹配與史密斯圓圖的基本原理資料免費(fèi)下載




 阻抗匹配和史密斯圖阻抗
阻抗匹配和史密斯圖阻抗










評論