本文旨在為沒(méi)有接觸過(guò)形式化方法的讀者提供一種新的視角看待計(jì)算機(jī)系統(tǒng)與算法，而非形式化方法或 TLA+ 教程。因此本文的重點(diǎn)是如何從數(shù)學(xué)角度思考程序，不會(huì)使用大篇幅講解 TLA+ 的語(yǔ)法。

1

我們?cè)撊绾螌?xiě)出正確的程序？

程序設(shè)計(jì)的目標(biāo)永遠(yuǎn)是寫(xiě)出正確的程序。隨著時(shí)間的推移，我們的程序越來(lái)越復(fù)雜，其中可能存在的錯(cuò)誤也越來(lái)越多。想要寫(xiě)出正確的程序，首先應(yīng)該了解程序中可能出現(xiàn)的錯(cuò)誤有哪些。

程序中會(huì)有什么樣錯(cuò)誤？

我將程序中可能出現(xiàn)的錯(cuò)誤粗略地分為兩類(lèi)：簡(jiǎn)單錯(cuò)誤與邏輯錯(cuò)誤。

簡(jiǎn)單錯(cuò)誤

簡(jiǎn)單錯(cuò)誤包含語(yǔ)義錯(cuò)誤、內(nèi)存錯(cuò)誤等。對(duì)于這些容易分析的簡(jiǎn)單錯(cuò)誤，我們已經(jīng)有很多成熟的方法與工具來(lái)避免，如編譯器、靜態(tài)分析工具、Garbage Collector 等。由于這類(lèi)錯(cuò)誤可以比較容易地被發(fā)現(xiàn)與修復(fù)，因此不是我們關(guān)注的重點(diǎn)。

邏輯錯(cuò)誤

邏輯錯(cuò)誤是程序中最難發(fā)現(xiàn)的錯(cuò)誤，也是最難修復(fù)的錯(cuò)誤，如死鎖、競(jìng)態(tài)條件、數(shù)據(jù)不一致等。邏輯錯(cuò)誤影響了程序的正確性、性能、可靠性等指標(biāo)，通常是由于程序的設(shè)計(jì)不夠完善導(dǎo)致的。對(duì)于這類(lèi)錯(cuò)誤，我們需要從更高的層面來(lái)分析與設(shè)計(jì)程序，而非僅僅從代碼的實(shí)現(xiàn)細(xì)節(jié)來(lái)考慮。

我們通常會(huì)使用一些方法來(lái)避免邏輯錯(cuò)誤，如：

• 優(yōu)化軟件架構(gòu)設(shè)計(jì)- 在設(shè)計(jì)階段就考慮程序的正確性，避免設(shè)計(jì)出不夠完善的程序
• 測(cè)試- 使用各種測(cè)試方法來(lái)減少程序的錯(cuò)誤，但無(wú)法保證程序的完全正確

越有經(jīng)驗(yàn)的人往往能想到更多的細(xì)節(jié)與可能性，設(shè)計(jì)出的系統(tǒng)通常更穩(wěn)定。但我們不能僅僅依賴(lài)于經(jīng)驗(yàn)：

• 經(jīng)驗(yàn)有局限性- 人類(lèi)的經(jīng)驗(yàn)是有限且不可靠的
• 復(fù)雜系統(tǒng)的行為、狀態(tài)太多- 一個(gè)復(fù)雜的系統(tǒng)，其行為與狀態(tài)太多，很難通過(guò)經(jīng)驗(yàn)來(lái)預(yù)測(cè)
• 特定程序?qū)φ_性的要求很高- 有些程序?qū)φ_性的要求很高，如金融系統(tǒng)、醫(yī)療系統(tǒng)等，這些程序的正確性很難通過(guò)經(jīng)驗(yàn)來(lái)保證
• 無(wú)法從理論上驗(yàn)證正確性- 只能盡量減少錯(cuò)誤的發(fā)生，但無(wú)法從理論上證明程序的正確性

綜上，我們需要一種更加嚴(yán)謹(jǐn)?shù)姆椒ǎ瑥脑O(shè)計(jì)上保證程序的正確性。

如果能夠從數(shù)學(xué)角度驗(yàn)證一個(gè)程序的正確性，就可以解決上述的問(wèn)題，這就是形式化方法的目標(biāo)。

形式化方法基于數(shù)學(xué)，通過(guò)為系統(tǒng)建立數(shù)學(xué)模型，來(lái)定義系統(tǒng)的行為、狀態(tài)等，然后定義系統(tǒng)的約束條件，如安全性、活性，最終證明模型滿(mǎn)足系統(tǒng)形式規(guī)約，來(lái)驗(yàn)證系統(tǒng)的正確性。對(duì)于有窮狀態(tài)的系統(tǒng)，可以使用以窮盡搜索為基礎(chǔ)的模型檢測(cè)，通過(guò)搜索待驗(yàn)證系統(tǒng)模型的有窮狀態(tài)空間來(lái)檢驗(yàn)該系統(tǒng)的行為是否具備預(yù)期屬性。對(duì)于有無(wú)窮狀態(tài)空間的系統(tǒng)，使用邏輯推理為基礎(chǔ)的演繹驗(yàn)證，利用歸納法驗(yàn)證系統(tǒng)的正確性。

本文用 TLA+ 語(yǔ)言作為工具來(lái)介紹形式化方法。

2

TLA+

TLA+ 的作者是在并發(fā)和分布式系統(tǒng)領(lǐng)域做出開(kāi)創(chuàng)性貢獻(xiàn)的 2013 年圖靈獎(jiǎng)獲得者，計(jì)算機(jī)科學(xué)家 Leslie Lamport。

TLA+ 是一種用于對(duì)程序和系統(tǒng)進(jìn)行建模的高級(jí)語(yǔ)言——尤其是并發(fā)和分布式程序和系統(tǒng)。其核心思想是：精確描述事物的最佳方式是使用簡(jiǎn)單的數(shù)學(xué)。TLA+ 及其工具可用于消除的設(shè)計(jì)錯(cuò)誤，這些錯(cuò)誤很難在代碼中發(fā)現(xiàn)并且糾正起來(lái)代價(jià)高昂。

使用 TLA+ 編寫(xiě)的 specification 并不是真正的工程代碼，無(wú)法用在生產(chǎn)環(huán)境中，因?yàn)?TLA+ 的目標(biāo)是在系統(tǒng)設(shè)計(jì)階段就發(fā)現(xiàn)并解決邏輯錯(cuò)誤。在 TLA+ 中，我們將程序抽象為有窮狀態(tài)的數(shù)學(xué)模型，通常是狀態(tài)機(jī)，然后利用 TLC Model Checker 窮盡程序所有可能到達(dá)的狀態(tài)并驗(yàn)證其正確性。

下面通過(guò)兩個(gè)簡(jiǎn)單的例子介紹 TLA+。這兩個(gè)例子均來(lái)自 TLA+ 作者的 Leslie Lamport's The TLA+ Video Course。本文的目標(biāo)是為沒(méi)有接觸過(guò)形式化方法的讀者提供一種新的視角看待計(jì)算機(jī)系統(tǒng)與算法，而不是 TLA+ 教程，因此不會(huì)過(guò)多介紹 TLA+ 的語(yǔ)法與工具的使用。

TLA+ 可以讓我們使用簡(jiǎn)單的數(shù)學(xué)抽象系統(tǒng)模型，主要是集合論與布爾邏輯。在抽象的過(guò)程中，我們要舍棄很多實(shí)現(xiàn)細(xì)節(jié)，僅關(guān)注程序的邏輯本身。

下面是一個(gè)簡(jiǎn)單的 C 語(yǔ)言程序，我們嘗試將其抽象為一個(gè) TLA+ 程序：

inti;
voidmain(){
i=someNumber();//someNumber()用來(lái)得到一個(gè)0到1000之間的數(shù)字
i=i+1;
}

我們需要將這個(gè)程序抽象為一個(gè)個(gè)獨(dú)立的狀態(tài)。很顯然，對(duì)于這個(gè)簡(jiǎn)單的程序，各狀態(tài)之間的不同點(diǎn)只有i的值。假設(shè)i在初始化后的默認(rèn)值是 0，且某次運(yùn)行這個(gè)程序時(shí)someNumber()返回了 42，那么這個(gè)程序存在的狀態(tài)轉(zhuǎn)換關(guān)系就是：

[i : 0] -> [i : 42] -> [i : 43]

這之中有三個(gè)狀態(tài)，每個(gè)狀態(tài)間的區(qū)別均為i的值不同。

這樣看似完成了抽象，但是這個(gè)抽象還是有問(wèn)題的。假設(shè)在另一次運(yùn)行中，someNumber()返回了 43，那么這個(gè)程序的狀態(tài)轉(zhuǎn)換關(guān)系就是：

[i : 0] -> [i : 43] -> [i : 44]

這與之前的抽象不符，因?yàn)閮纱芜\(yùn)行的狀態(tài)轉(zhuǎn)換關(guān)系不同。這是因?yàn)槲覀儧](méi)有考慮到someNumber()的返回值。

程序的"狀態(tài)"是指程序運(yùn)行完成各個(gè)階段后的時(shí)間點(diǎn)，而不是程序運(yùn)行的過(guò)程。因此，每個(gè)狀態(tài)都是獨(dú)立的，且狀態(tài)之間的轉(zhuǎn)換都是原子的。這與傳統(tǒng)的編程有很大的區(qū)別，因?yàn)閭鹘y(tǒng)的編程是面向過(guò)程的，而 TLA+ 是面向狀態(tài)的。我們只在乎目前程序運(yùn)行到了什么狀態(tài)，因此可以引入一個(gè)變量pc來(lái)表示程序運(yùn)行到了哪個(gè)階段，這樣我們就可以清晰地表示程序的次態(tài)關(guān)系：

inti;
voidmain(){
i=someNumber();//pc="start"
i=i+1;//pc="middle"
}//pc="done"

[pc : start] -> [pc : middle] -> [pc : done]

i的初始值為 0，pc的初始值為start，我們可以把次態(tài)關(guān)系寫(xiě)成：

其中，對(duì)于變量i，它的下一個(gè)狀態(tài)表示為i'，這是 TLA+ 中定義變量狀態(tài)轉(zhuǎn)換的方式。i' ∈ 0..1000代表i在下一個(gè)狀態(tài)的值是 0 到 1000 之間的一個(gè)數(shù)，也就是someNumber()，0..1000代表集合{0,1,...,1000}。∧是布爾邏輯中的邏輯與，可以認(rèn)為意為"并且"。最終程序運(yùn)行完成，不會(huì)再有下一個(gè)狀態(tài)，因此表示為FALSE。

在 TLA+ 中，我們編寫(xiě)的是一個(gè)個(gè)狀態(tài)。因此，并非是"因?yàn)?/span>pc = start所以i' ∈ 0..1000"，事實(shí)上兩者的關(guān)系是并列的：**在這個(gè)狀態(tài)中，pc的值是start并且i下一個(gè)狀態(tài)的值∈ 0..1000**。有了這樣的思想，我們可以將上面的抽象改寫(xiě)為：

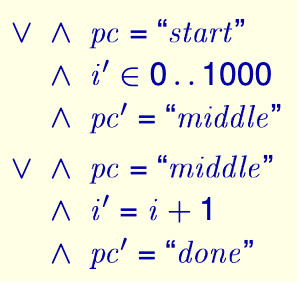
• EXTENDS用于引入其他 specification 中定義的 module，這里引入了標(biāo)準(zhǔn)庫(kù)中的Integers，主要用在i' ∈ 0..1000上。
• VARIABLES用于定義變量，這里定義了i和pc。
• Init用于定義初始狀態(tài)，這里定義了i = 0和pc = "start"。
• Next用于定義狀態(tài)轉(zhuǎn)換關(guān)系。

二階段提交（英語(yǔ)：Two-phase Commit）是指在計(jì)算機(jī)網(wǎng)絡(luò)以及數(shù)據(jù)庫(kù)領(lǐng)域內(nèi)，為了使基于分布式系統(tǒng)架構(gòu)下的所有節(jié)點(diǎn)在進(jìn)行事務(wù)提交時(shí)保持一致性而設(shè)計(jì)的一種算法。通常，二階段提交也被稱(chēng)為是一種協(xié)議（Protocol）。在分布式系統(tǒng)中，每個(gè)節(jié)點(diǎn)雖然可以知曉自己的操作時(shí)成功或者失敗，卻無(wú)法知道其他節(jié)點(diǎn)的操作的成功或失敗。當(dāng)一個(gè)事務(wù)跨越多個(gè)節(jié)點(diǎn)時(shí)，為了保持事務(wù)的ACID特性，需要引入一個(gè)作為協(xié)調(diào)者的組件來(lái)統(tǒng)一掌控所有節(jié)點(diǎn)（稱(chēng)作參與者）的操作結(jié)果并最終指示這些節(jié)點(diǎn)是否要把操作結(jié)果進(jìn)行真正的提交（比如將更新后的數(shù)據(jù)寫(xiě)入磁盤(pán)等等）。因此，二階段提交的算法思路可以概括為：參與者將操作成敗通知協(xié)調(diào)者，再由協(xié)調(diào)者根據(jù)所有參與者的反饋情報(bào)決定各參與者是否要提交操作還是中止操作。——Two-Phase Commit (Wikipedia)

在Leslie Lamport's The TLA+ Video Course中，Lamport 以這樣的方式類(lèi)比解釋 Two-Phase Commit：

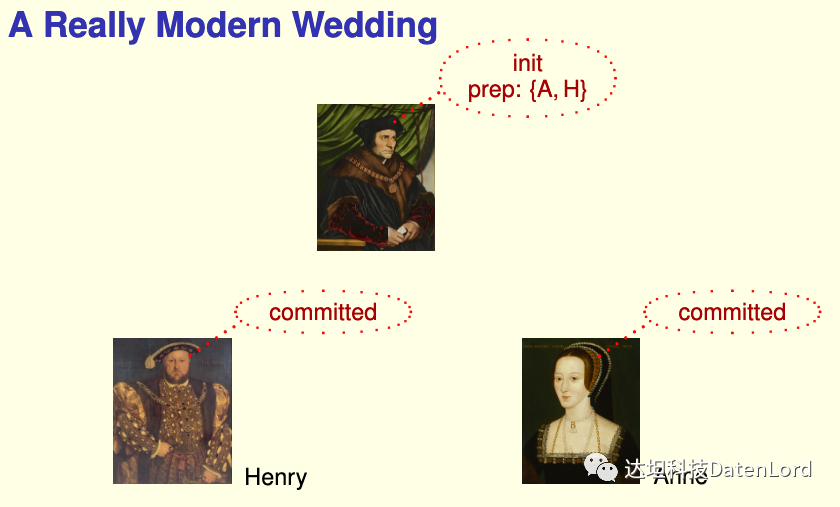
在婚禮上，牧師是協(xié)調(diào)者，新郎和新娘是參與者。當(dāng)新郎和新娘都同意婚事時(shí)，牧師才會(huì)正式宣布婚事。如果有一方不同意，牧師就會(huì)中止婚事：

1. 牧師問(wèn)新郎：你是否同意這件婚事？
2. 新郎回答：我同意（prepared）。
3. 牧師問(wèn)新娘：你是否同意這件婚事？
4. 新娘回答：我同意（prepared）。
5. 牧師宣布：婚事正式成立（committed）。

如果其中有一方不同意，牧師就會(huì)中止（abort）婚事。

在數(shù)據(jù)庫(kù)中，Transaction Manager 是協(xié)調(diào)者（牧師）。當(dāng) Transaction Manager 詢(xún)問(wèn)所有參與者 Resource Managers （新郎 / 新娘）時(shí)，如果所有 Resource Managers 都同意提交事務(wù)，Transaction Manager 就會(huì)把事務(wù)提交。如果有一方不同意，Transaction Manager 就會(huì)中止事務(wù)。

Two-Phase Commit 的詳細(xì)介紹與流程可以在Wikipedia上找到。

首先我們來(lái)定義一些常量與變量以及其初始狀態(tài)：

• 常量RM是所有 Resource Manager 標(biāo)識(shí)的集合，例如可以設(shè)為集合{"r1", "r2", "r3"}。
• 變量rmState用于記錄每個(gè) Resource Manager 的狀態(tài)，用rmState[r]表示r的狀態(tài)，有working、prepared、committed、aborted四種狀態(tài)，每個(gè)RM的初始狀態(tài)均為working。
• 變量tmState用于記錄 Transaction Manager 的狀態(tài)，有init、committed、aborted三種狀態(tài)，初始狀態(tài)為init。
• 變量tmPrepared用于記錄已經(jīng)準(zhǔn)備好（處于prepared狀態(tài)）的 Resource Manager，初始值是一個(gè)空集。
• 變量msgs作為消息池，用于記錄所有正在傳輸?shù)南ⅲ跏贾凳且粋€(gè)空集。

下面我們來(lái)定義系統(tǒng)做可能發(fā)生的動(dòng)作。

• TLA+ 中可以用上述方式定義類(lèi)似于其它編程語(yǔ)言中"函數(shù)"概念的表達(dá)式，這樣就無(wú)需對(duì)每一個(gè) Resource Manager 都定義一個(gè)表達(dá)式了。
• [type → "prepare", rm → r]是一個(gè) TLA+ 中的 record，類(lèi)似于其它編程語(yǔ)言中的 struct。
• UNCHANGED ?rmState, tmState, msgs?表示這個(gè)動(dòng)作不會(huì)改變rmState、tmState、msgs這三個(gè)變量的值。在 TLA+ 中，每一個(gè)變量的值是否改變都需要顯式地聲明。

當(dāng)TM的狀態(tài)為init，且在消息池中存在來(lái)自r的Prepared消息，tmPrepared在下一個(gè)狀態(tài)的值會(huì)是tmPrepared和{r}的并集。

上述 4 個(gè) Resource Manager 動(dòng)作分別是 Resource Manager 選擇 Prepare 與 Abort，以及處理由 Transaction Manager 決定的 Commit 與 Abort。

其中，存在語(yǔ)法如rmState' = [rmState except ![r] = "prepared"]，意為"在下一個(gè)狀態(tài)中，rmState[r]的值變?yōu)?/span>prepared，其它部分不變"。

如果我們用形如rmState[r]' = "prepared"的形式來(lái)表示，我們并沒(méi)有顯式地說(shuō)明rmState的其它部分在下一個(gè)狀態(tài)的值，因此是不正確的。

TLA+ 與我們通常編寫(xiě)的程序不同，是數(shù)學(xué)。在編程中，我們會(huì)使用到數(shù)組，而在 TLA+ 中，我們使用函數(shù)來(lái)表達(dá)類(lèi)似的概念，數(shù)組的下標(biāo)組成的集合就是函數(shù)的定義域。

編寫(xiě)完系統(tǒng)可能存在的所有動(dòng)作后，我們就可以開(kāi)始?xì)w納系統(tǒng)的狀態(tài)轉(zhuǎn)換了：

其中，我們使用存在量詞?r ∈ RM來(lái)表示"對(duì)于集合RM的任意元素r，都存在這種行為"。TLA+ 的狀態(tài)轉(zhuǎn)換是原子的，因此在一個(gè)狀態(tài)中這個(gè)"或"分支內(nèi)只會(huì)有一個(gè)r被選擇，這可以類(lèi)比為編程語(yǔ)言中的for r in RM，但在本質(zhì)上不同。

至此，對(duì)系統(tǒng)的建模就完成了。下面我們需要編寫(xiě)系統(tǒng)的約束條件：

{
[r1|->"working",r2|->"working"],
[r1|->"working",r2|->"prepared"],
[r1|->"working",r2|->"committed"],
...
[r1|->"aborted",r2|->"committed"],
[r1|->"aborted",r2|->"aborted"]
}

{
[type|->"Prepared",rm|->r1],
[type|->"Prepared",rm|->r2],
...
}最

最后的約束條件Consistent用于保證系統(tǒng)的一致性：在任意時(shí)刻，系統(tǒng)中不可能存在兩個(gè) Resource Managers 分別處于committed和abort狀態(tài)。

最終，我們將約束條件作為不變量，與系統(tǒng)模型一起交給 TLC Model Checker 進(jìn)行驗(yàn)證，就可以證明系統(tǒng)的正確性。

3

總結(jié)