先給大家講個(gè)笑話(huà)樂(lè)呵一下：

有一天阿東到圖書(shū)館借了 N 本書(shū)，出圖書(shū)館的時(shí)候，警報(bào)響了，于是保安把阿東攔下，要檢查一下哪本書(shū)沒(méi)有登記出借。阿東正準(zhǔn)備把每一本書(shū)在報(bào)警器下過(guò)一下，以找出引發(fā)警報(bào)的書(shū)，但是保安露出不屑的眼神：你連二分查找都不會(huì)嗎？于是保安把書(shū)分成兩堆，讓第一堆過(guò)一下報(bào)警器，報(bào)警器響；于是再把這堆書(shū)分成兩堆…… 最終，檢測(cè)了 logN 次之后，保安成功的找到了那本引起警報(bào)的書(shū)，露出了得意和嘲諷的笑容。于是阿東背著剩下的書(shū)走了。

從此，圖書(shū)館丟了 N - 1 本書(shū)。

二分查找真的很簡(jiǎn)單嗎？并不簡(jiǎn)單。看看 Knuth 大佬（發(fā)明 KMP 算法的那位）怎么說(shuō)的：

“

Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky...

這句話(huà)可以這樣理解：思路很簡(jiǎn)單，細(xì)節(jié)是魔鬼。

本文就來(lái)探究幾個(gè)最常用的二分查找場(chǎng)景：尋找一個(gè)數(shù)、尋找左側(cè)邊界、尋找右側(cè)邊界。

而且，我們就是要深入細(xì)節(jié)，比如不等號(hào)是否應(yīng)該帶等號(hào)，mid 是否應(yīng)該加一等等。分析這些細(xì)節(jié)的差異以及出現(xiàn)這些差異的原因，保證你能靈活準(zhǔn)確地寫(xiě)出正確的二分查找算法。

零、二分查找框架

int binarySearch(int[] nums, int target) {
    int left = 0, right = ...;

    while(...) {
        int mid = (right + left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;
}

分析二分查找的一個(gè)技巧是：不要出現(xiàn) else，而是把所有情況用 else if 寫(xiě)清楚，這樣可以清楚地展現(xiàn)所有細(xì)節(jié) 。 本文都會(huì)使用 else if，旨在講清楚，讀者理解后可自行簡(jiǎn)化。

其中...標(biāo)記的部分，就是可能出現(xiàn)細(xì)節(jié)問(wèn)題的地方，當(dāng)你見(jiàn)到一個(gè)二分查找的代碼時(shí)，首先注意這幾個(gè)地方。后文用實(shí)例分析這些地方能有什么樣的變化。

另外聲明一下，計(jì)算 mid 時(shí)需要技巧防止溢出，可以 [參見(jiàn)前文]，本文暫時(shí)忽略這個(gè)問(wèn)題。

一、尋找一個(gè)數(shù)（基本的二分搜索）

這個(gè)場(chǎng)景是最簡(jiǎn)單的，可能也是大家最熟悉的，即搜索一個(gè)數(shù)，如果存在，返回其索引，否則返回 -1。

int binarySearch(int[] nums, int target) {
    int left = 0; 
    int right = nums.length - 1; // 注意

    while(left <= right) { // 注意
        int mid = (right + left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; // 注意
        else if (nums[mid] > target)
            right = mid - 1; // 注意
        }
    return -1;
}

1 . 為什么 while 循環(huán)的條件中是 <=，而不是 < ？

答：因?yàn)槌跏蓟?right 的賦值是 nums.length - 1，即最后一個(gè)元素的索引，而不是 nums.length。

這二者可能出現(xiàn)在不同功能的二分查找中，區(qū)別是：前者相當(dāng)于兩端都閉區(qū)間 [left, right]，后者相當(dāng)于左閉右開(kāi)區(qū)間 [left, right)，因?yàn)樗饕笮?nums.length 是越界的。

我們這個(gè)算法中使用的是 [left, right] 兩端都閉的區(qū)間。 這個(gè)區(qū)間就是每次進(jìn)行搜索的區(qū)間，我們不妨稱(chēng)為「搜索區(qū)間」 。

什么時(shí)候應(yīng)該停止搜索呢？當(dāng)然，找到了目標(biāo)值的時(shí)候可以終止：

if(nums[mid] == target)
        return mid;

但如果沒(méi)找到，就需要 while 循環(huán)終止，然后返回 -1。那 while 循環(huán)什么時(shí)候應(yīng)該終止？ 搜索區(qū)間為空的時(shí)候應(yīng)該終止 ，意味著你沒(méi)得找了，就等于沒(méi)找到嘛。

while(left <= right)的終止條件是 left == right + 1，寫(xiě)成區(qū)間的形式就是 [right + 1, right]，或者帶個(gè)具體的數(shù)字進(jìn)去 [3, 2]，可見(jiàn) 這時(shí)候搜索區(qū)間為空 ，因?yàn)闆](méi)有數(shù)字既大于等于 3 又小于等于 2 的吧。所以這時(shí)候 while 循環(huán)終止是正確的，直接返回 -1 即可。

while(left < right)的終止條件是 left == right，寫(xiě)成區(qū)間的形式就是 [right, right]，或者帶個(gè)具體的數(shù)字進(jìn)去 [2, 2]， 這時(shí)候搜索區(qū)間非空 ，還有一個(gè)數(shù) 2，但此時(shí) while 循環(huán)終止了。也就是說(shuō)這區(qū)間 [2, 2] 被漏掉了，索引 2 沒(méi)有被搜索，如果這時(shí)候直接返回 -1 就可能出現(xiàn)錯(cuò)誤。

當(dāng)然，如果你非要用 while(left < right) 也可以，我們已經(jīng)知道了出錯(cuò)的原因，就打個(gè)補(bǔ)丁好了：

//...
while(left < right) {
    // ...
}
return nums[left] == target ? left : -1;

2 . 為什么 left = mid + 1，right = mid - 1？我看有的代碼是 right = mid 或者 left = mid，沒(méi)有這些加加減減，到底怎么回事，怎么判斷？

答：這也是二分查找的一個(gè)難點(diǎn)，不過(guò)只要你能理解前面的內(nèi)容，就能夠很容易判斷。

剛才明確了「搜索區(qū)間」這個(gè)概念，而且本算法的搜索區(qū)間是兩端都閉的，即 [left, right]。那么當(dāng)我們發(fā)現(xiàn)索引 mid 不是要找的 target 時(shí)，如何確定下一步的搜索區(qū)間呢？

當(dāng)然是去搜索 [left, mid - 1] 或者 [mid + 1, right] 對(duì)不對(duì)？因?yàn)?mid 已經(jīng)搜索過(guò)，應(yīng)該從搜索區(qū)間中去除。

3 . 此算法有什么缺陷？

答：至此，你應(yīng)該已經(jīng)掌握了該算法的所有細(xì)節(jié)，以及這樣處理的原因。但是，這個(gè)算法存在局限性。

比如說(shuō)給你有序數(shù)組 nums = [1,2,2,2,3]，target = 2，此算法返回的索引是 2，沒(méi)錯(cuò)。但是如果我想得到 target 的左側(cè)邊界，即索引 1，或者我想得到 target 的右側(cè)邊界，即索引 3，這樣的話(huà)此算法是無(wú)法處理的。

這樣的需求很常見(jiàn)。你也許會(huì)說(shuō)，找到一個(gè) target 索引，然后向左或向右線(xiàn)性搜索不行嗎？可以，但是不好，因?yàn)檫@樣難以保證二分查找對(duì)數(shù)級(jí)的復(fù)雜度了。

我們后續(xù)的算法就來(lái)討論這兩種二分查找的算法。

二、尋找左側(cè)邊界的二分搜索

直接看代碼，其中的標(biāo)記是需要注意的細(xì)節(jié)：

int left_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0;
    int right = nums.length; // 注意

    while (left < right) { // 注意
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid; // 注意
        }
    }
    return left;
}

1. 為什么 while(left < right) 而不是 <= ?

答：用相同的方法分析，因?yàn)槌跏蓟?right = nums.length 而不是 nums.length - 1 。因此每次循環(huán)的「搜索區(qū)間」是 [left, right) 左閉右開(kāi)。

while(left < right) 終止的條件是 left == right，此時(shí)搜索區(qū)間 [left, left) 恰巧為空，所以可以正確終止。

2. 為什么沒(méi)有返回 -1 的操作？如果 nums 中不存在 target 這個(gè)值，怎么辦？

答：因?yàn)橐徊揭徊絹?lái)，先理解一下這個(gè)「左側(cè)邊界」有什么特殊含義：

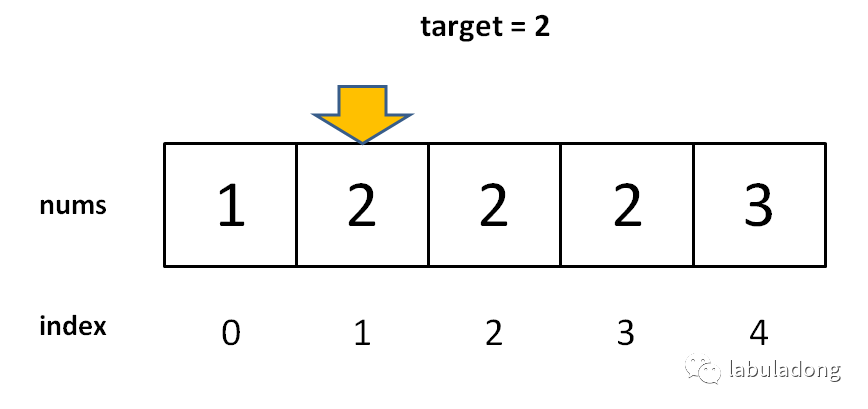
對(duì)于這個(gè)數(shù)組，算法會(huì)返回 1。這個(gè) 1 的含義可以這樣解讀：nums 中小于 2 的元素有 1 個(gè)。

比如對(duì)于有序數(shù)組 nums = [2,3,5,7], target = 1，算法會(huì)返回 0，含義是：nums 中小于 1 的元素有 0 個(gè)。如果 target = 8，算法會(huì)返回 4，含義是：nums 中小于 8 的元素有 4 個(gè)。

綜上可以看出，函數(shù)的返回值（即 left 變量的值）取值區(qū)間是閉區(qū)間 [0, nums.length]，所以我們簡(jiǎn)單添加兩行代碼就能在正確的時(shí)候 return -1：

while (left < right) {
    //...
}
// target 比所有數(shù)都大
if (left == nums.length) return -1;
// 類(lèi)似之前算法的處理方式
return nums[left] == target ? left : -1;

3. 為什么 left = mid + 1，right = mid ？和之前的算法不一樣？

答：這個(gè)很好解釋?zhuān)驗(yàn)槲覀兊摹杆阉鲄^(qū)間」是 [left, right) 左閉右開(kāi)，所以當(dāng) nums[mid] 被檢測(cè)之后，下一步的搜索區(qū)間應(yīng)該去掉 mid 分割成兩個(gè)區(qū)間，即 [left, mid) 或 [mid + 1, right)。

4. 為什么該算法能夠搜索左側(cè)邊界？

答：關(guān)鍵在于對(duì)于 nums[mid] == target 這種情況的處理：

if (nums[mid] == target)
        right = mid;

可見(jiàn)，找到 target 時(shí)不要立即返回，而是縮小「搜索區(qū)間」的上界 right，在區(qū)間 [left, mid) 中繼續(xù)搜索，即不斷向左收縮，達(dá)到鎖定左側(cè)邊界的目的。

5. 為什么返回 left 而不是 right？

答：都是一樣的，因?yàn)?while 終止的條件是 left == right。

三、尋找右側(cè)邊界的二分查找

尋找右側(cè)邊界和尋找左側(cè)邊界的代碼差不多，只有兩處不同，已標(biāo)注：

int right_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0, right = nums.length;

    while (left < right) {
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            left = mid + 1; // 注意
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left - 1; // 注意}

1. 為什么這個(gè)算法能夠找到右側(cè)邊界？

答：類(lèi)似地，關(guān)鍵點(diǎn)還是這里：

if (nums[mid] == target) {
        left = mid + 1;

當(dāng) nums[mid] == target 時(shí)，不要立即返回，而是增大「搜索區(qū)間」的下界 left，使得區(qū)間不斷向右收縮，達(dá)到鎖定右側(cè)邊界的目的。

*2. *為什么最后返回 left - 1 而不像左側(cè)邊界的函數(shù)，返回 left？而且我覺(jué)得這里既然是搜索右側(cè)邊界，應(yīng)該返回 right 才對(duì)。

答：首先，while 循環(huán)的終止條件是 left == right，所以 left 和 right 是一樣的，你非要體現(xiàn)右側(cè)的特點(diǎn)，返回 right - 1 好了。

至于為什么要減一，這是搜索右側(cè)邊界的一個(gè)特殊點(diǎn)，關(guān)鍵在這個(gè)條件判斷：

if (nums[mid] == target) {
        left = mid + 1;
        // 這樣想: mid = left - 1

因?yàn)槲覀儗?duì) left 的更新必須是 left = mid + 1，就是說(shuō) while 循環(huán)結(jié)束時(shí)，nums[left] 一定不等于 target 了，而 nums[left - 1] 可能是 target。

至于為什么 left 的更新必須是 left = mid + 1，同左側(cè)邊界搜索，就不再贅述。

*3. *為什么沒(méi)有返回 -1 的操作？如果 nums 中不存在 target 這個(gè)值，怎么辦？

答：類(lèi)似之前的左側(cè)邊界搜索，因?yàn)?while 的終止條件是 left == right，就是說(shuō) left 的取值范圍是 [0, nums.length]，所以可以添加兩行代碼，正確地返回 -1：

while (left < right) {
    // ...
}
if (left == 0) return -1;
return nums[left-1] == target ? (left-1) : -1;

四、最后總結(jié)

先來(lái)梳理一下這些細(xì)節(jié)差異的因果邏輯：

第一個(gè)，最基本的二分查找算法：

因?yàn)槲覀兂跏蓟?right = nums.length - 1
所以決定了我們的「搜索區(qū)間」是 [left, right]
所以決定了 while (left <= right)
同時(shí)也決定了 left = mid+1 和 right = mid-1

因?yàn)槲覀冎恍枵业揭粋€(gè) target 的索引即可
所以當(dāng) nums[mid] == target 時(shí)可以立即返回

第二個(gè)，尋找左側(cè)邊界的二分查找：

因?yàn)槲覀兂跏蓟?right = nums.length
所以決定了我們的「搜索區(qū)間」是 [left, right)
所以決定了 while (left < right)
同時(shí)也決定了 left = mid+1 和 right = mid

因?yàn)槲覀冃枵业?target 的最左側(cè)索引
所以當(dāng) nums[mid] == target 時(shí)不要立即返回
而要收緊右側(cè)邊界以鎖定左側(cè)邊界

第三個(gè)，尋找右側(cè)邊界的二分查找：

因?yàn)槲覀兂跏蓟?right = nums.length
所以決定了我們的「搜索區(qū)間」是 [left, right)
所以決定了 while (left < right)
同時(shí)也決定了 left = mid+1 和 right = mid

因?yàn)槲覀冃枵业?target 的最右側(cè)索引
所以當(dāng) nums[mid] == target 時(shí)不要立即返回
而要收緊左側(cè)邊界以鎖定右側(cè)邊界

又因?yàn)槭站o左側(cè)邊界時(shí)必須 left = mid + 1
所以最后無(wú)論返回 left 還是 right，必須減一

如果以上內(nèi)容你都能理解，那么恭喜你，二分查找算法的細(xì)節(jié)不過(guò)如此。

通過(guò)本文，你學(xué)會(huì)了：

1. 分析二分查找代碼時(shí)，不要出現(xiàn) else，全部展開(kāi)成 else if 方便理解。

2. 注意「搜索區(qū)間」和 while 的終止條件，如果存在漏掉的元素，記得在最后檢查。

3. 如需要搜索左右邊界，只要在 nums[mid] == target 時(shí)做修改即可。搜索右側(cè)時(shí)需要減一。

就算遇到其他的二分查找變形，運(yùn)用這幾點(diǎn)技巧，也能保證你寫(xiě)出正確的代碼。LeetCode Explore 中有二分查找的專(zhuān)項(xiàng)練習(xí)，其中提供了三種不同的代碼模板，現(xiàn)在你再去看看，很容易就知道這幾個(gè)模板的實(shí)現(xiàn)原理了。