線性判別分析(LDA)是一種降維技術,其目標是將數據集投影到較低維度空間中。線性判別分析也被稱為正態判別分析(NDA)或判別函數分析,是Fisher線性判別的推廣。
線性判別分析(LDA)和主成分分析(PCA)都是常用的線性變換技術,用于降低數據的維度。
PCA可以描述為“無監督”算法,因為它“忽略”類別標簽,其目標是找到最大化數據集方差的方向(所謂的主成分)。
與PCA不同,LDA是“有監督的”,它計算出能夠最大化多個類別之間間隔的軸(“線性判別”)。
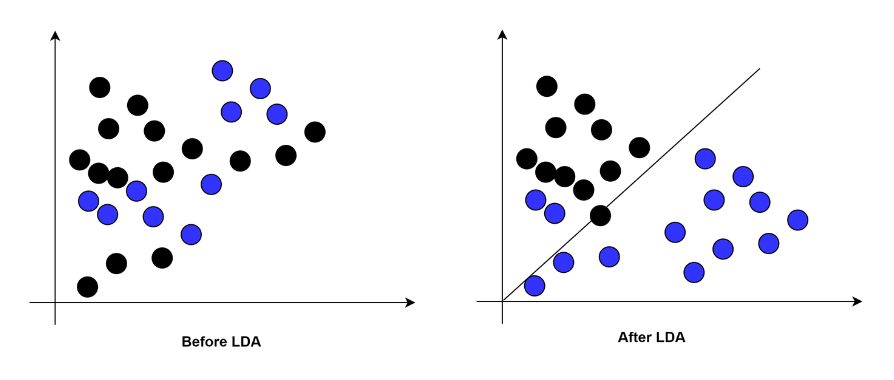
LDA是如何工作的?
LDA使用Fisher線性判別方法來區分類別。
Fisher線性判別是一種分類方法,它將高維數據投影到一維空間中,并在這個一維空間中進行分類。
投影最大化類別均值之間的距離,同時最小化每個類別內部的方差。
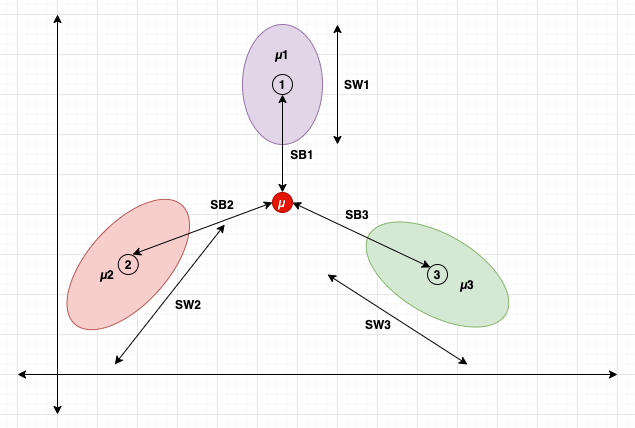
類別:1、2和3
類別均值:μ1、μ2和μ3
類別間散布:SB1、SB2和SB3
類別內散布:SW1、SW2和SW3
數據集均值:μ
它的思想是最大化類別間散布SB,同時最小化類別內散布SW。
數學公式
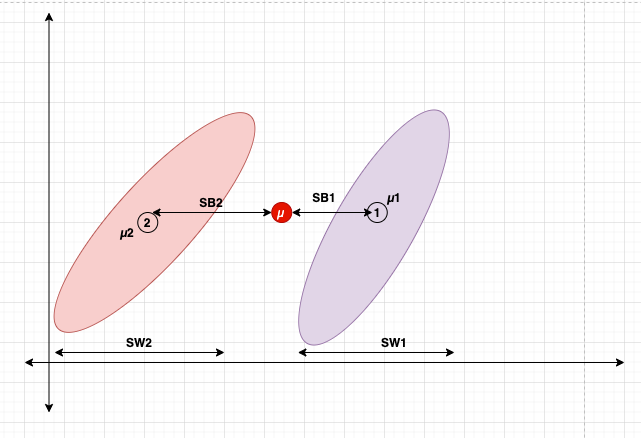

動機
-
尋找一個方向,可以放大類間差異。
-
最大化投影后的均值之間的(平方)差異。
(通過找到最大化類別均值之間差異的方向,LDA可以有效地將數據投影到一個低維子空間中,其中類別更容易分離)
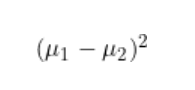
-
最小化每個類別內的投影散布
(通過找到最大化類別均值之間差異的方向,LDA可以有效地將數據投影到一個低維子空間中,其中類別更容易分離)
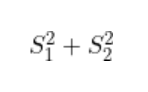
散布
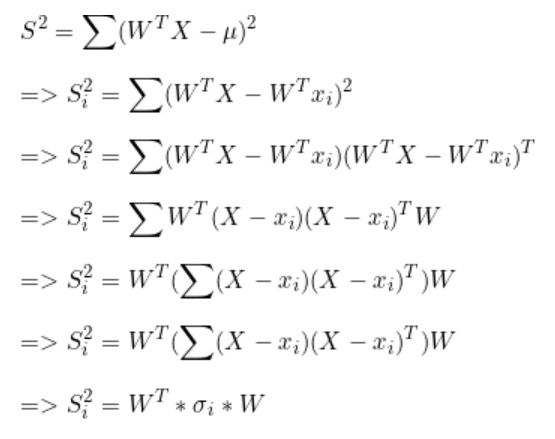

均值差異
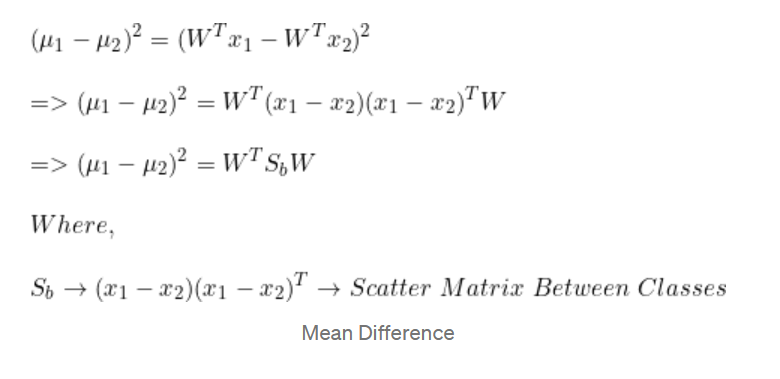
散布差異

Fischer 指數
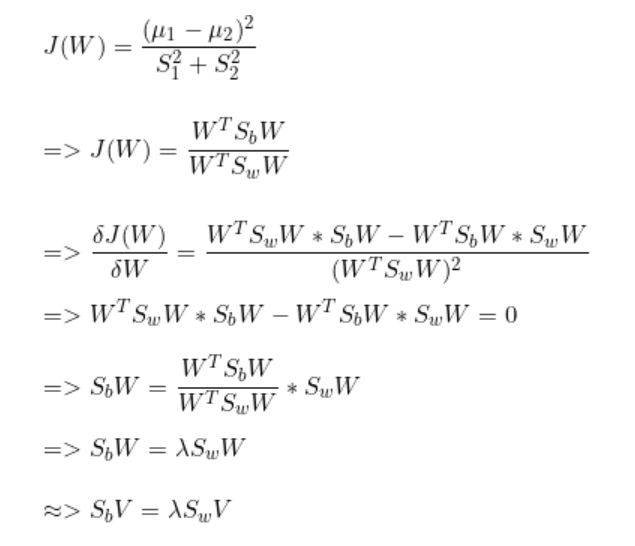

這意味著在選擇特征值時,我們將始終選擇C-1個特征值及其相應的特征向量。其中,C為數據集中的類別數。
例子
**數據集
**
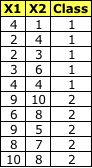
步驟1:計算類內散布矩陣(SW)

計算每個類別的協方差矩陣
類別1:
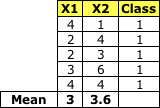
Class 1
均值矩陣:

協方差:

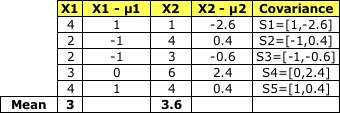
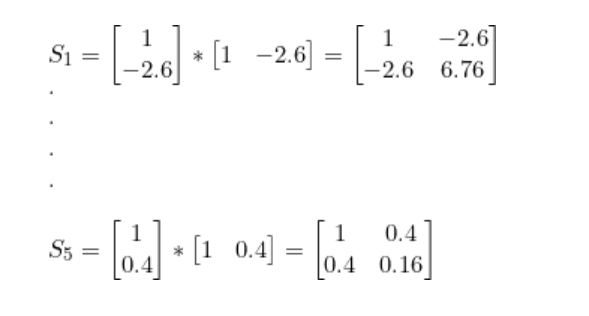
將S1到 S5加在一起就得到了 Sc1
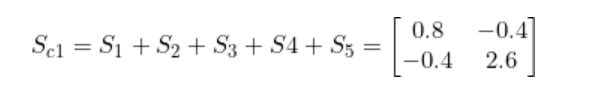
類別2:
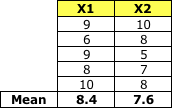
Class 2
均值矩陣:
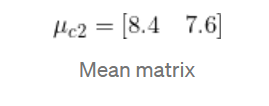
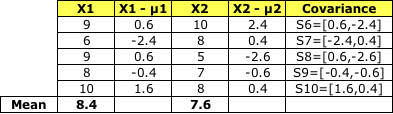
和 Sc1一樣, 將S6 到S10加到一起, 就得到了協方差 Sc2 -
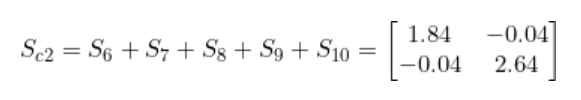
將Sc1和Sc2相加就得到了類內散布矩陣Sw。
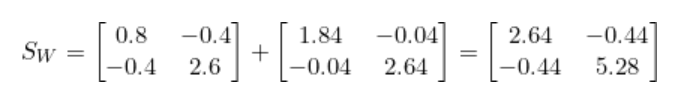
步驟2:計算類間散布矩陣(SB)
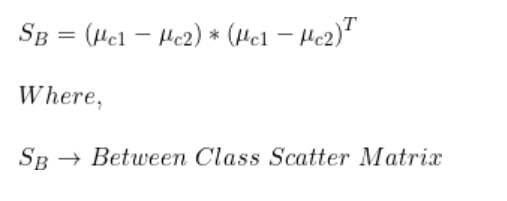
我們已經有了類別1和類別2每個特征的均值。
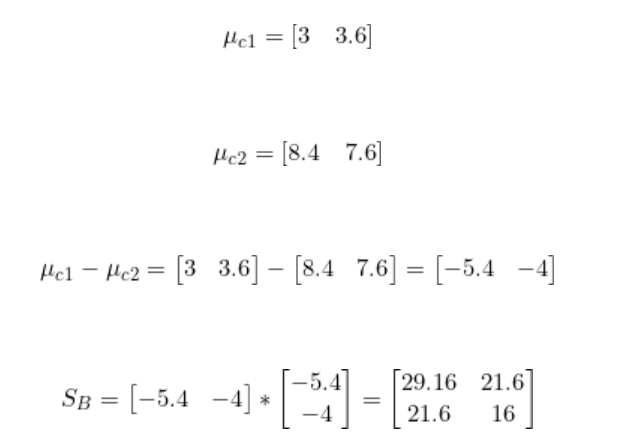
步驟3:找到最佳LDA投影向量
與PCA類似,我們使用具有最大特征值的特征向量來找到最佳投影向量。該特征向量可以用以下形式表示。
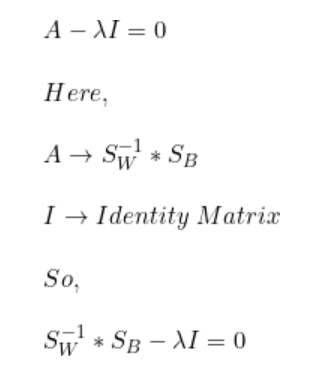
我們已經計算得到了SB和SW。
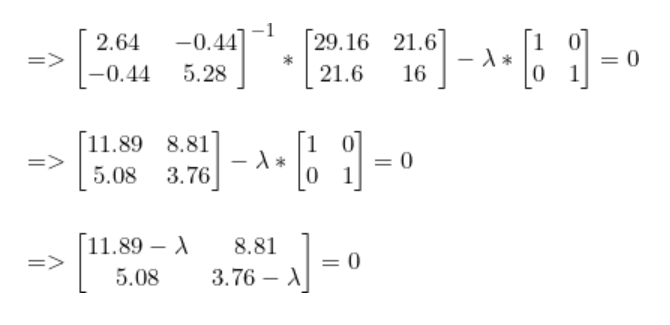
解出lambda后,我們得到最高值lambda = 15.65。現在,對于每個lambda值,解出相應的向量。
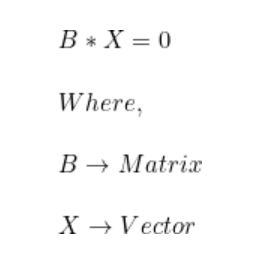
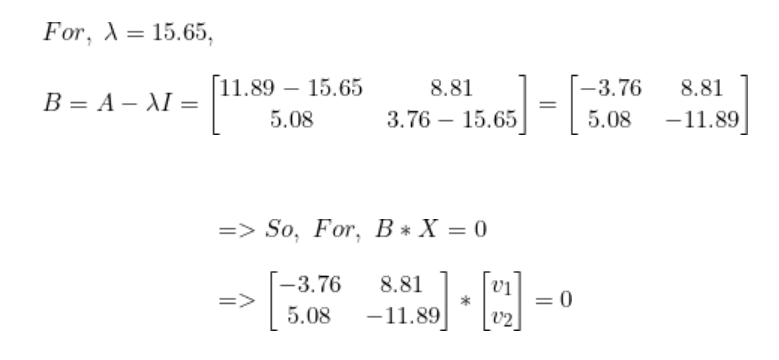
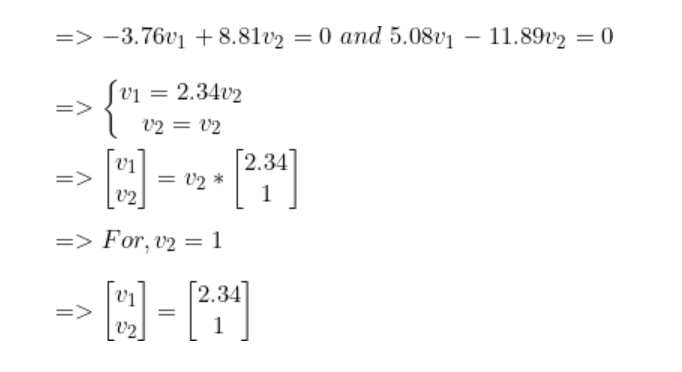
步驟4:將樣本轉換到新子空間上。

因此,使用LDA我們進行了如下轉換。
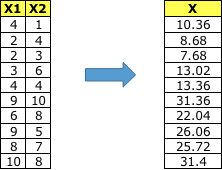
-
函數
+關注
關注
3文章
4346瀏覽量
62972 -
線性
+關注
關注
0文章
199瀏覽量
25200 -
LDA
+關注
關注
0文章
29瀏覽量
10647
發布評論請先 登錄
相關推薦
基于核函數的Fisher判別分析算法在人耳識別中的應用
近鄰邊界Fisher判別分析
人臉識別經典算法三:Fisherface(LDA)
核局部Fisher判別分析的行人重識別
基于逐步判別分析的血液氣味識別





 線性判別分析LDA背后的數學原理
線性判別分析LDA背后的數學原理











評論