根據機器學習相關介紹(10)——支持向量機(低維到高維的映射),支持向量機可通過引入φ(x)函數,將低維線性不可分問題轉換為高維線性可分問題。轉換后支持向量機的優化問題可改寫為:
最小化:1/2||ω||2+C∑δi或1/2||ω||2+C∑δi2,
限制條件:(1)δi≥0,i=1~N;(2)yi(ωTφ(Xi)+b)≥1-δi,i=1~N。
欲求解上述優化問題,需先知道φ(x)的形式。
但支持向量機的創始人Vladimir Vapnik提出結論:完成測試樣本的類別預測不必須知道φ(x)的具體形式,如果對任意兩個向量X1、X2已知:
K(X1,X2)=φ(X1)Tφ(X2)
則仍可以完成測試樣本的類別預測(具體如何完成在下篇文章中敘述)。
上式中K(X1,X2)被定義為核函數(Kernel Function),核函數是一個實數(上式中φ(X1)Tφ(X2)為兩個維度相同的行向量和列向量相乘的形式,其結果為一個實數)。
上述結論成立的一個必要條件是核函數K與低維到高維映射φ(x)具有一一對應的關系,即只有核函數K與映射φ(x)一一對應關系,核函數K才能代替φ(x)完成測試樣本的類別預測。
一般情況下,核函數K與映射φ(x)具有一一對應關系,下文以兩個案例說明核函數K與映射φ(x)的一一對應關系。
案例一:
假設:φ(x)是一個將二維向量映射為三維向量的映射,其中,二維向量X=[x1,x2]T,映射φ(x)=φ([x1,x2]T)=[x12,x1x2,x22];
再假設:X1=[x11,x12]T,X2=[x21,x22]T;
則φ(X1)=[x112,x11x12,x122],φ(X2)=[x212,x21x22,x222];
若核函數K(X1,X2)=φ(X1)Tφ(X2),則K(X1,X2)=[x112,x11x12,x122][x212,x21x22,x222]T=x112x212+x11x12x21x22+x122x222。
案例二:
假設:K(X1,X2)
=(x11x21+x12x22+1)2
=x112x212+x122x222+2x11x12x21x22+2x11x21+2x12x22
=φ(X1)Tφ(X2);
再假設:X=[x1,x2]T;
則φ(x)=φ([x1,x2]T)=[x12,x22,1,√2x1x2,√2x1,√2x2]T(該式中√代表根號,該式推導過程暫不知,若將X1=[x11,x12]T,X2=[x21,x22]T代入該式,再通過φ(X1)Tφ(X2)=K(X1,X2),可反推導出案例二中的核函數),φ(x)中各維度值可相互交換順序。
但當核函數不能轉化為兩個φ(x)內積形式時,核函數與映射φ(x)不具有一一對應關系。因此,核函數需可以轉化為兩個φ(x)內積形式。
K(X1,X2)可轉化為φ(X1)Tφ(X2)(即可轉化為兩個φ(x)內積形式)的充要條件:
(1)K(X1,X2)=K(X2,X1)(即核函數具有交換性)
(2)對于任意的Ci(i=1~N)和任意的N,有:
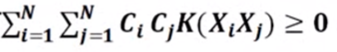
即核函數K具有半正定性。
審核編輯:劉清
-
向量機
+關注
關注
0文章
166瀏覽量
20924 -
機器學習
+關注
關注
66文章
8438瀏覽量
133080
原文標題:機器學習相關介紹(11)——支持向量機(核函數的定義)
文章出處:【微信號:行業學習與研究,微信公眾號:行業學習與研究】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
SUMIF函數與SUMIFS函數的區別
高斯卷積核函數在圖像采樣中的意義
高斯濾波的卷積核怎么確定
面試常考+1:函數指針與指針函數、數組指針與指針數組

Labview實現自定義四維云圖(三維曲面圖像)可視化顯示
函數信號發生器的定義、功能及應用
微軟Dev Home應用提供自定義文件管理支持
飛騰信息技術有限公司:復數向量卷積處理技術及設備
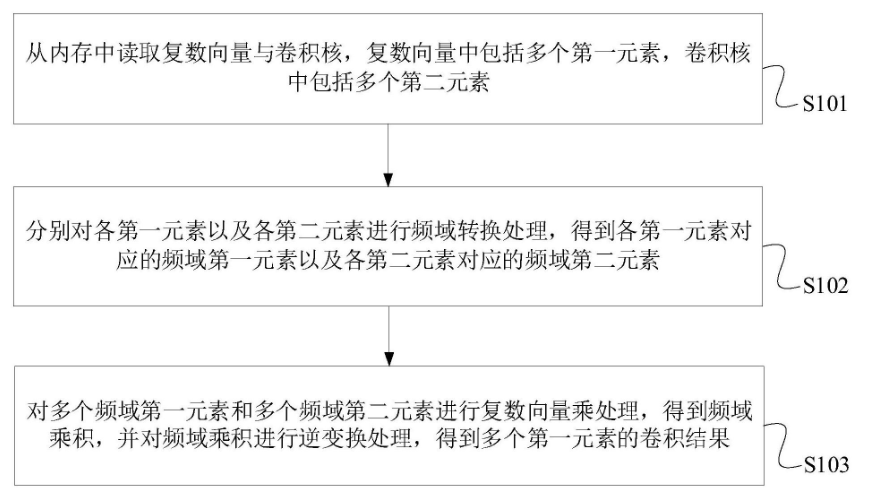




 支持向量機(核函數的定義)
支持向量機(核函數的定義)










評論