來源：古月居

KNN(k-Nearest Neighbors)思想簡單，應(yīng)用的數(shù)學(xué)知識幾乎為0，所以作為機(jī)器學(xué)習(xí)的入門非常實(shí)用、可以解釋機(jī)器學(xué)習(xí)算法使用過程中的很多細(xì)節(jié)問題。能夠更加完整地刻畫機(jī)器學(xué)習(xí)應(yīng)用的流程。

首先大致介紹一下KNN的思想，假設(shè)我們現(xiàn)在有兩類數(shù)據(jù)集，一類是紅色的點(diǎn)表示，另一類用藍(lán)色的點(diǎn)表示，這兩類點(diǎn)就作為我們的訓(xùn)練數(shù)據(jù)集，當(dāng)有一個新的數(shù)據(jù)綠色的點(diǎn)，那么我們該怎么給這個綠色的點(diǎn)進(jìn)行分類呢？

一般情況下，我們需要先指定一個k，當(dāng)一個新的數(shù)據(jù)集來臨時，我們首先計(jì)算這個新的數(shù)據(jù)跟訓(xùn)練集中的每一個數(shù)據(jù)的距離，一般使用歐氏距離。

然后從中選出距離最近的k個點(diǎn)，這個k一般選取為奇數(shù)，方便后面投票決策。在k個點(diǎn)中根據(jù)最多的確定新的數(shù)據(jù)屬于哪一類。

KNN基礎(chǔ)

1.先創(chuàng)建好數(shù)據(jù)集x_train, y_train，和一個新的數(shù)據(jù)x_new, 并使用matplot將其可視化出來。

import numpy as np
import matplotlib.pyplot as plt


raw_data_x = [[3.3935, 2.3313],
       [3.1101, 1.7815],
       [1.3438, 3.3684],
       [3.5823, 4.6792],
       [2.2804, 2.8670],
       [7.4234, 4.6965],
       [5.7451, 3.5340],
       [9.1722, 2.5111],
       [7.7928, 3.4241],
       [7.9398, 0.7916]]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
x_train = np.array(raw_data_x)
y_train = np.array(raw_data_y)


x_new = np.array([8.0936, 3.3657])


plt.scatter(x_train[y_train==0,0], x_train[y_train==0,1], color='g')
plt.scatter(x_train[y_train==1,0], x_train[y_train==1,1], color='r')
plt.scatter(x_new[0], x_new[1], color='b')
plt.show()

1.knn過程

2.計(jì)算距離

from math import sqrt
distance = []
for x in x_train:
  d = sqrt(np.sum((x_new - x) ** 2))
  distance.append(d)


# 其實(shí)上面這些代碼用一行就可以搞定
# distances = [sqrt(np.sum((x_new - x) ** 2)) for x in x_train]

輸出結(jié)果：

[10.888422144185997,
 11.825242797930196,
 15.18734646375067,
 11.660703691887552,
 12.89974598548359,
 12.707715895864213,
 9.398411207752083,
 15.62480440229573,
 12.345673749536719,
 14.394770082568183]

將距離進(jìn)行排序,返回的是排序之后的索引位置

nearsest = np.argsort(distances)

輸出結(jié)果：array([6, 0, 3, 1, 8, 5, 4, 9, 2, 7], dtype=int64)

取k個點(diǎn)，假設(shè)k=5

k = 5
topk_y = [y_train[i] for i in nearest[:k]]
topk_y

輸出結(jié)果：[1, 0, 0, 0, 1]

根據(jù)輸出結(jié)果我們可以發(fā)現(xiàn)，新來的數(shù)據(jù)距離最近的5個點(diǎn)，有三個點(diǎn)屬于第一類，有兩個點(diǎn)屬于第二類，根據(jù)少數(shù)服從多數(shù)原則，新來的數(shù)據(jù)就屬于第一類！

投票

from collections import Counter
Counter(topk_y)

輸出結(jié)果：Counter({1: 2, 0: 3})

votes = Counter(topk_y)
votes.most_common(1)
y_new = votes.most_common(1)[0][0]

輸出結(jié)果：0

這樣，我們就完成了一個基本的knn！

自己寫一個knn函數(shù)

knn是一個不需要訓(xùn)練過程的機(jī)器學(xué)習(xí)算法。其數(shù)據(jù)集可以近似看成一個模型。

import numpy as np
from math import sqrt
from collections import Counter


def kNN_classifier(k, x_train, y_train, x_new):


  assert 1 <= k <= x_train.shape[0], "k must be valid"
 ? ?assert x_train.shape[0] == y_train.shape[0], "the size of x_train must be equal to the size of y_train"
 ? ?assert x_train.shape[1] == x_new.shape[0], "the feature number of x_new must be equal to x_train"


 ? ?distances = [sqrt(np.sum((x_new - x) ** 2)) for x in x_train]
 ? ?nearest = np.argsort(distances)


 ? ?topk_y = [y_train[i] for i in nearest[:k]]
 ? ?votes = Counter(topk_y)


 ? ?return votes.most_common(1)[0][0]

測試一下：

raw_data_x = [[3.3935, 2.3313],
       [3.1101, 1.7815],
       [1.3438, 3.3684],
       [3.5823, 4.6792],
       [2.2804, 2.8670],
       [7.4234, 4.6965],
       [5.7451, 3.5340],
       [9.1722, 2.5111],
       [7.7928, 3.4241],
       [7.9398, 0.7916]]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
x_train = np.array(raw_data_x)
y_train = np.array(raw_data_y)


x_new = np.array([8.0936, 3.3657])


y_new = kNN_classifier(5, x_train, y_train, x_new)
print(y_new)

使用sklearn中的KNN

from sklearn.neighbors import KNeighborsClassifier
import numpy as np


raw_data_x = [[3.3935, 2.3313],
       [3.1101, 1.7815],
       [1.3438, 3.3684],
       [3.5823, 4.6792],
       [2.2804, 2.8670],
       [7.4234, 4.6965],
       [5.7451, 3.5340],
       [9.1722, 2.5111],
       [7.7928, 3.4241],
       [7.9398, 0.7916]]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
x_train = np.array(raw_data_x)
y_train = np.array(raw_data_y)


x_new = np.array([8.0936, 3.3657])


knn_classifier = KNeighborsClassifier(n_neighbors=5)
knn_classifier.fit(x_train, y_train)


y_new = knn_classifier.predict(x_new.reshape(1, -1))
print(y_new[0])

自己寫一個面向?qū)ο蟮腒NN

import numpy as np
from math import sqrt
from collections import Counter


class KNNClassifier():


  def __init__(self, k):
    assert 1 <= k, "k must be valid"
 ? ? ? ?self.k = k
 ? ? ? ?self._x_train = None
 ? ? ? ?self._y_train = None


 ? ?def fit(self, x_train, y_train):
 ? ? ? ?assert x_train.shape[0] == y_train.shape[0],  
 ? ? ? ?"the size of x_train must be equal to the size of y_train"
 ? ? ? ?assert self.k <= x_train.shape[0],  
 ? ? ? ? "the size of x_train must be at least k"


 ? ? ? ?self._x_train = x_train
 ? ? ? ?self._y_train = y_train
 ? ? ? ?return self


 ? ?def predict(self, x_new):
 ? ? ? ?x_new = x_new.reshape(1, -1)
 ? ? ? ?assert self._x_train is not None and self._y_train is not None, 
 ? ? ? ?"must fit before predict"
 ? ? ? ?assert x_new.shape[1] == self._x_train.shape[1], 
 ? ? ? ?"the feature number of x must be equal to x_train"


 ? ? ? ?y_new = [self._predict(x) for x in x_new]
 ? ? ? ?return np.array(y_new)


 ? ?def _predict(self, x):
 ? ? ? ?assert x.shape[0] == self._x_train.shape[1], 
 ? ? ? ?"the feature number of x must be equal to x_train"


 ? ? ? ?distances = [sqrt(np.sum((x_train - x) ** 2)) for x_train in self._x_train]
 ? ? ? ?nearest = np.argsort(distances)


 ? ? ? ?topk_y = [self._y_train[i] for i in nearest[:self.k]]
 ? ? ? ?votes = Counter(topk_y)


 ? ? ? ?return votes.most_common(1)[0][0]


 ? ?def __repr__(self):
 ? ? ? ?return "KNN(k=%d)" % self.k

測試一下：

raw_data_x = [[3.3935, 2.3313],
       [3.1101, 1.7815],
       [1.3438, 3.3684],
       [3.5823, 4.6792],
       [2.2804, 2.8670],
       [7.4234, 4.6965],
       [5.7451, 3.5340],
       [9.1722, 2.5111],
       [7.7928, 3.4241],
       [7.9398, 0.7916]]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
x_train = np.array(raw_data_x)
y_train = np.array(raw_data_y)


x_new = np.array([8.0936, 3.3657])


knn_clf = KNNClassifier(6)
knn_clf.fit(x_train, y_train)
y_new = knn_clf.predict(x_new)
print(y_new[0])

分割數(shù)據(jù)集

import numpy as np
from sklearn import datasets




def train_test_split(x, y, test_ratio=0.2, seed=None):


  assert x.shape[0] == y.shape[0], "the size of x must be equal to the size of y"
  assert 0.0 <= test_ratio <= 1.0, "test_ratio must be valid"


 ? ?if seed:
 ? ? ? ?np.random.seed(seed)


 ? ?shuffle_idx = np.random.permutation(len(x))


 ? ?test_size = int(len(x) * test_ratio)
 ? ?test_idx = shuffle_idx[:test_size]
 ? ?train_idx = shuffle_idx[test_size:]


 ? ?x_train = x[train_idx]
 ? ?y_train = y[train_idx]


 ? ?x_test = x[test_idx]
 ? ?y_test = y[test_idx]


 ? ?return x_train, y_train, x_test, y_test

sklearn中鳶尾花數(shù)據(jù)測試KNN

import numpy as np
from sklearn import datasets
from knn_clf import KNNClassifier


iris = datasets.load_iris()
x = iris.data
y = iris.target


x_train, y_train, x_test, y_test = train_test_split(x, y)
my_knn_clf = KNNClassifier(k=3)
my_knn_clf.fit(x_train, y_train)


y_predict = my_knn_clf.predict(x_test)
print(sum(y_predict == y_test))
print(sum(y_predict == y_test) / len(y_test))
# 也可以使用sklearn中自帶的數(shù)據(jù)集拆分方法
from sklearn.model_selection import train_test_split
import numpy as np
from sklearn import datasets
from knn_clf import KNNClassifier


iris = datasets.load_iris()
x = iris.data
y = iris.target
x_train, y_train, x_test, y_test = train_test_split(x, y, 
                          test_size=0.2, random_state=666)
my_knn_clf = KNNClassifier(k=3)
my_knn_clf.fit(x_train, y_train)
y_predict = my_knn_clf.predict(x_test)
print(sum(y_predict == y_test))
print(sum(y_predict == y_test) / len(y_test))

sklearn中手寫數(shù)字?jǐn)?shù)據(jù)集測試KNN

首先，先來了解一下手寫數(shù)字?jǐn)?shù)據(jù)集。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets


digits = datasets.load_digits()
digits.keys()
print(digits.DESCR)
y.shape
digits.target_names
y[:100]
x[:10]
some_digit = x[666]
y[666]
some_digit_image = some_digit.reshape(8, 8)
plt.imshow(some_digit_image, cmap=plt.cm.binary)
plt.show()

接下來，就開始動手試試。

from sklearn import datasets
from shuffle_dataset import train_test_split
from knn_clf import KNNClassifier


digits = datasets.load_digits()
x = digits.data
y = digits.target


x_train, y_train, x_test, y_test = train_test_split(x, y, test_ratio=0.2)
my_knn_clf = KNNClassifier(k=3)
my_knn_clf.fit(x_train, y_train)
y_predict = my_knn_clf.predict(x_test)


print(sum(y_predict == y_test) / len(y_test))

把求acc封裝成一個函數(shù)，方便調(diào)用。

def accuracy_score(y_true, y_predict):
  assert y_true.shape[0] == y_predict.shape[0],  
  "the size of y_true must be equal to the size of y_predict"


  return sum(y_true == y_predict) / len(y_true)

接下來把它封裝到KNNClassifier的類中。

import numpy as np
from math import sqrt
from collections import Counter
from metrics import accuracy_score


class KNNClassifier():


  def __init__(self, k):
    assert 1 <= k, "k must be valid"
 ? ? ? ?self.k = k
 ? ? ? ?self._x_train = None
 ? ? ? ?self._y_train = None


 ? ?def fit(self, x_train, y_train):
 ? ? ? ?assert x_train.shape[0] == y_train.shape[0], 
 ? ? ? ?"the size of x_train must be equal to the size of y_train"
 ? ? ? ?assert self.k <= x_train.shape[0], 
 ? ? ? ?"the size of x_train must be at least k"


 ? ? ? ?self._x_train = x_train
 ? ? ? ?self._y_train = y_train
 ? ? ? ?return self


 ? ?def predict(self, x_new):
 ? ? ? ?# x_new = x_new.reshape(1, -1)
 ? ? ? ?assert self._x_train is not None and self._y_train is not None, 
 ? ? ? ?"must fit before predict"
 ? ? ? ?assert x_new.shape[1] == self._x_train.shape[1], 
 ? ? ? ?"the feature number of x must be equal to x_train"


 ? ? ? ?y_new = [self._predict(x) for x in x_new]
 ? ? ? ?return np.array(y_new)


 ? ?def _predict(self, x):
 ? ? ? ?assert x.shape[0] == self._x_train.shape[1], 
 ? ? ? ?"the feature number of x must be equal to x_train"


 ? ? ? ?distances = [sqrt(np.sum((x_train - x) ** 2)) for x_train in self._x_train]
 ? ? ? ?nearest = np.argsort(distances)


 ? ? ? ?topk_y = [self._y_train[i] for i in nearest[:self.k]]
 ? ? ? ?votes = Counter(topk_y)


 ? ? ? ?return votes.most_common(1)[0][0]


 ? ?def score(self, x_test, y_test):
 ? ? ? ?y_predict = self.predict(x_test)
 ? ? ? ?return accuracy_score(y_test, y_predict)


 ? ?def __repr__(self):
 ? ? ? ?return "KNN(k=%d)" % self.k

其實(shí)，在sklearn中這些都已經(jīng)封裝好了。

from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier


digits = datasets.load_digits()
x = digits.data
y = digits.target


x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
knn_classifier = KNeighborsClassifier(n_neighbors=3)
knn_classifier.fit(x_train, y_train)
knn_classifier.score(x_test, y_test)

超參數(shù)

k

在knn中的超參數(shù)k何時最優(yōu)？

from sklearn.metrics import accuracy_score 
from sklearn.model_selection import train_test_split 
from sklearn.neighbors import KNeighborsClassifier 


digits = datasets.load_digits() 
x = digits.data 
y = digits.target 
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2) 


best_score = 0.0 
best_k = -1 
for k in range(1, 11): 
  knn_clf = KNeighborsClassifier(n_neighbors=k) 
  knn_clf.fit(x_train, y_train) 
  score = knn_clf.score(x_test, y_test) 
  if score > best_score: 
    best_k = k 
    best_score = score 
print("best k=", best_k) print("best score=", best_score)

投票方式

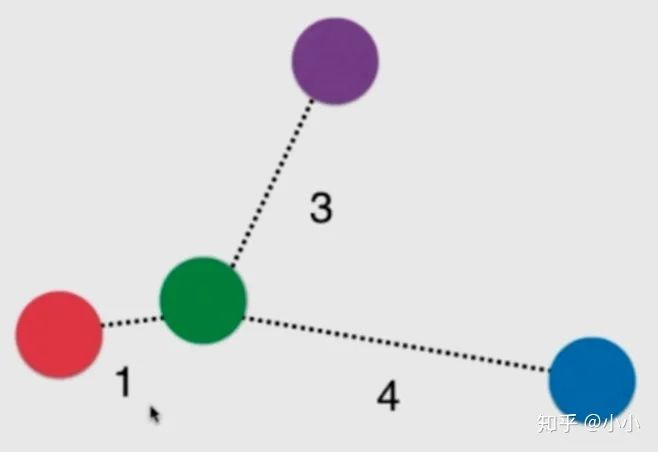
上面這張圖，綠色的球最近的三顆球分別是紅色的1號，紫色的3號和藍(lán)色的4號。如果只考慮綠色的k個近鄰中多數(shù)服從少數(shù)，目前來說就是平票。

即使不是平票，紅色也是距離綠色最近。此時我們就可以考慮給他們加個權(quán)重。一般使用距離的倒數(shù)作為權(quán)重。假設(shè)距離分別為1、 3、 4

紅球：1 紫+藍(lán)：1/3 + 1/4 = 7/12

這兩者加起來都沒有紅色的權(quán)重大，因此最終將這顆綠球歸為紅色類別。這樣能有效解決平票問題。 因此，這也算knn的一個超參數(shù)。

其實(shí)這個在sklearn封裝的knn中已經(jīng)考慮到了這個問題。在KNeighborsClassifier(n_neighbors=k，weights=？)

還有一個參數(shù)weights，一般有兩種：uniform、distance。

from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier


digits = datasets.load_digits()
x = digits.data
y = digits.target


x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)


best_method = ""
best_score = 0.0
best_k = -1
for method in["uniform", "distance"]: 
  for k in range(1, 11):
    knn_clf = KNeighborsClassifier(n_neighbors=k, weights=method)
    knn_clf.fit(x_train, y_train)
    score = knn_clf.score(x_test, y_test)
    if score > best_score:
      best_method = method
      best_k = k
      best_score = score
print("best_method=", best_method)
print("best k=", best_k)
print("best score=", best_score)

p

如果使用距離，那么有很多種距離可以使用，歐氏距離、曼哈頓距離、明可夫斯基距離。

from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier


digits = datasets.load_digits()
x = digits.data
y = digits.target


x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)


best_p = -1
best_score = 0.0
best_k = -1
for p in range(1, 6):
  for k in range(1, 11):
    knn_clf = KNeighborsClassifier(n_neighbors=k, weights="distance", p=p)
    knn_clf.fit(x_train, y_train)
    score = knn_clf.score(x_test, y_test)
    if score > best_score:
      best_p = p
      best_k = k
      best_score = score
print("best_p=", best_p)
print("best k=", best_k)
print("best score=", best_score)