前言

在研究運放形成的反饋系統時，相位裕度是衡量穩定性的一個重要指標。因此，明確相位裕度與運放的開環，環路，閉環響應的關系是一個重要的問題，有助于我們更好地在穩定性，功耗，速度之間進行折衷考慮。

巴克豪森判據

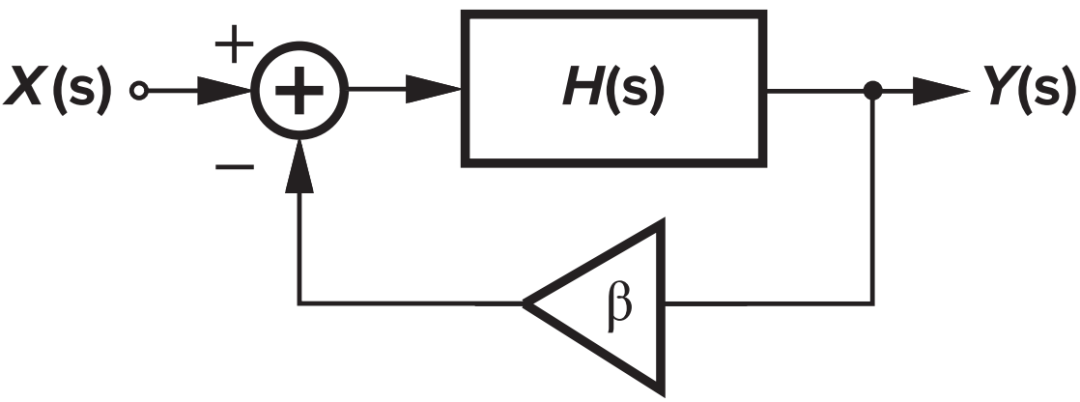
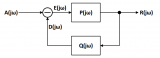
圖1 基本負反饋系統

如上圖所示的負反饋系統，假定圖中β是頻率無關的常數(β通常由電阻分壓，電容分壓等方式形成，大部分情況下是頻率無關的)，該閉環傳輸函數可寫為 式(1) ：

其中β為反饋系數，H(s)是開環響應，βH(s)為環路響應。

若在一個頻率ω1處，環路響應βH(s=jω 1 )=-1，則閉環“增益”趨于無窮大，電路可以放大自身的噪聲直到它最終開始振蕩，該條件可以分別表達為**式(2) **和式** (3)**

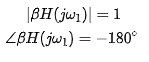
上述就是 巴克豪森判據 。

從巴克豪森判據可以看出，判斷反饋系統是否穩定主要取決于環路響應βH(s)。然而，有時候我們在設計運放時，通常是將開環響應GBW頻率處的剩余相位當作相位裕度（即單位增益相位裕度），這是一種所有反饋系數β下的最差相位裕度。這樣設計對可能使用在各種情況下的通用運放來說沒問題的，但對于芯片內部一些反饋環路固定不變的情況，便會存在過設計，造成一些性能浪費，在本文的后面章節關于該問題將進行更為詳細的分析。

相位裕度

使環路增益幅值等于1的頻率點為“增益交點頻率”，GX，使環路增益相位等于-180°的頻率點為“相位交點頻率”，PX。要保證系統的穩定，PX必須遠于GX，且兩者間距越大，反饋系統越穩定。而相位裕度PM，就是描述當GX出現時，距離PX出現剩余的相位，從而反應兩者的距離。

相位裕度與開環，環路，閉環響應的關系

圖2 相位裕度與開環，環路，閉環響應的關系

正如上文所言，相位裕度主要取決于環路響應，那么相位裕度和開環響應，閉環響應之間的關系是怎樣的呢，本節對這個問題進行分析。本文以一個次主極點位于GBW外的兩極點運放組成的反饋系統作為研究對象，如圖2所示，自上至下三幅圖分別為三個不同反饋系數的環路響應，閉環響應以及運放的開環相位（也為環路相位）圖。圖中運放的響應A即為上文反饋系統中的H。

首先觀察圖2(a)和圖2(c)，在(a)中，環路增益βA open =1(0dB)的點(GX)即為它們的曲線與橫坐標的交點。從β1至β3值逐漸變大，GX出現得逐漸變晚。由于反饋系數通常小于1，因此β 3 =1是這個系統可能出現的最晚的GX。對應到圖2(c)中，β1至β3對應的相位裕度PM1~PM3逐漸減小。因此可以得到結論：反饋系數越大，相位裕度越小。

由于β 3 =1，所以圖2(a)中β3Aopen的曲線就是運放的開環增益曲線。我們在設計運放時，常常通過檢查GBW處剩余的相位作為運放的相位裕度，實際上得到的就是該運放在β 3 =1這個相位裕度最壞情況下的值。

圖2(b)中給出了反饋系統的閉環增益，從式(1)可知，開環增益Aopen與閉環增益Aclose之間的差約為環路增益βA open (取dB之前相除等于取dB之后相減)，因此βA open =1(0dB)的點應為Aopen與Aclose重新交合的點（也為閉環主極點位置），如圖中所示，將其對應到圖2(c)后可以得到與之前相同的結論。

對運放設計的參考

我們在設計一個運放時，通常使用單位增益相位裕度作為指標進行設計。通過上文的分析可知，這種方式得到的相位裕度是運放在所有可能的反饋情況下的最差值。對于一個通用運放，運放可能被應用在各種反饋系數下，因此這樣設計可以確保運放在所有反饋情況下都是穩定的。但假如對于一個固定反饋系數的運放，比如IC設計時內部各個環路使用的運放，假如反饋系數小于1，實際的相位裕度比上述方法得到的相位裕度要大，因此相位裕度實際上被過設計了，這樣實際上造成了固定速度下功耗的浪費或者固定功耗下速度的浪費。

以設計兩級運放為例，過設計的相位裕度導致了過設計的密勒補償電容，從而造成輸入級電流或運放帶寬的浪費。

因此，對固定反饋系數的運放，實際上我們可以回歸巴克豪森判據的本質，去找屬于該反饋系數的環路響應的GX，從而設計相位裕度，而不是直接去設計單位增益相位裕度。

總結

本文分析了相位裕度與運放的開環響應，環路響應，閉環響應的關系，為讀者在設計運放的相位裕度時提供一些理論參考，不足之處請多多指正。