大多數示波器上都有個FFT功能,也叫快速傅立葉變換,但很多人不了解這個功能是做什么用的,百度以后又會遇到各種各樣的高數公式,看的一頭霧水,遂而放棄這塊知識。

我們來看百度百科的解釋:
FFT,即為快速傅氏變換,是離散傅氏變換的快速算法,它是根據離散傅氏變換的奇、偶、虛、實等特性,對離散傅立葉變換的算法進行改進獲得的。
這一看,頭都大了。
今天我們就帶大家簡單的了解下什么是傅里葉變換以及它的功能作用。
本文不會涉及任何數學公式,目的只在讓大家能理解傅里葉變換表達的是什么,至于怎么來的,我們不管。
理解傅立葉變換基本原理:
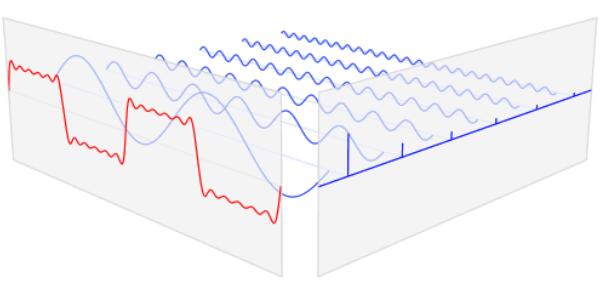
傅立葉變換認為,任何復雜的信號都是由多個正余弦波疊加而來的。
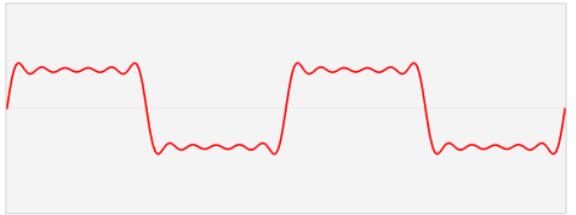
比如這個紅色信號,我們就可以看作是多個藍色正余弦波在垂直向量上的疊加。
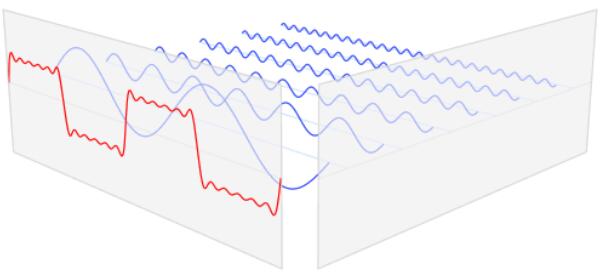
大家都知道秤和砝碼吧?我們要量物品的重量,就可以用一個一個砝碼來標稱。這里,這一個個藍色的正余弦波就是砝碼,這個紅色的信號就是被測物品。傅立葉變換,就是這桿秤。
通過傅立葉變換,我們可以把這一個個看不見的藍色信號給抓出來。
再比如,光也是一種波,自然光也是由不同顏色的光疊加而成的。通過傅立葉變換,可以把不同頻率的光從自然光中給區分出來。

還有,假設你處在一個嘈雜的環境中,各種各樣的聲音一起進入你的耳朵,這個嘈雜的聲音的聲波實際也就是由環境中各種各樣聲音的聲波組合起來的。通過傅立葉變換,可以把不同頻率的聲音從嘈雜聲中給區分出來。
理解頻域:
我們活在這個世界,對周圍萬物的感受,可以說都是在時間軸上的感受。聽音樂、畫畫、跳舞,看著你的孩子一天天長高,觀察股市的變化等等,都是建立在時間上變化的,世間萬物都隨時間不停變化。以時間為參考系去看待這個世界,我們就叫它時域分析。示波器上的信號亦是如此,電壓大小隨時間變化。這就是時域。
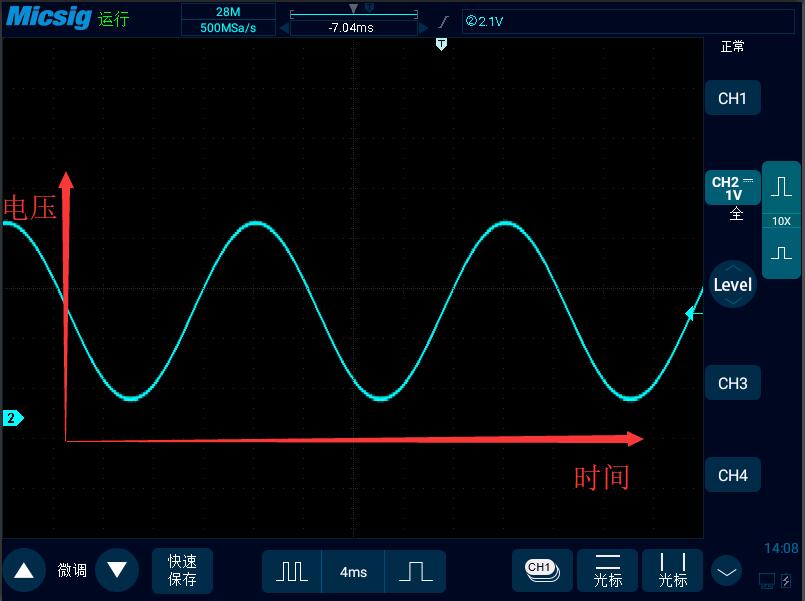
那么,什么是頻域呢?顧名思義,頻域就是以頻率作為參考系去觀察的世界。
還記得這個圖不?
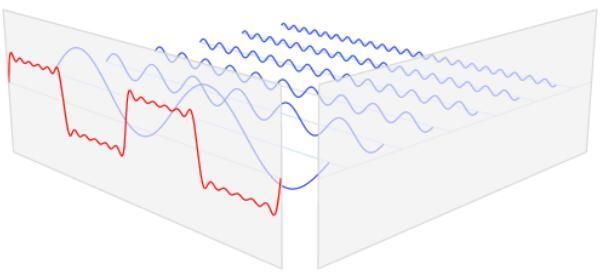
這里,每個被分出來的藍色信號都有不同的頻率,每個信號有不同的電壓值。如果我們把這些信號的頻率作為X軸,電壓值作為Y軸,就會是下面這樣:
這個圖,就是FFT后我們看到的圖。這就是頻域。
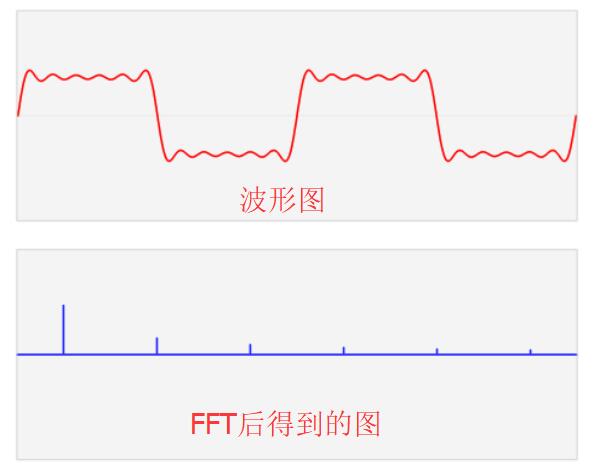
我們上面所學全部匯成一個圖,就是下面這樣:

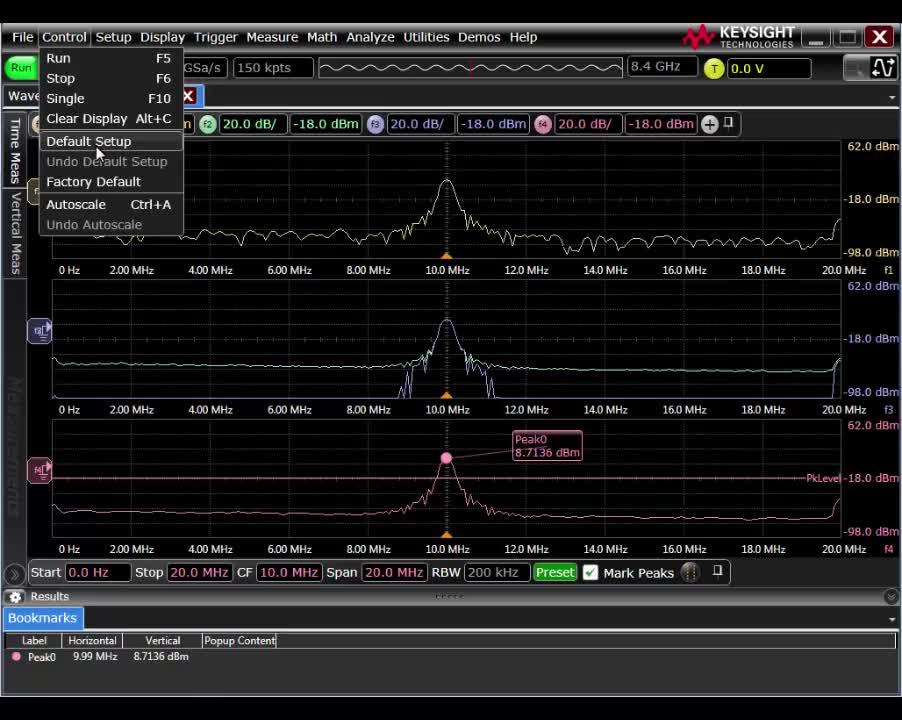
示波器實操測量:
下面這個信號是示波器的校準方波信號,我們打開FFT功能可以看到這個信號的頻譜圖。
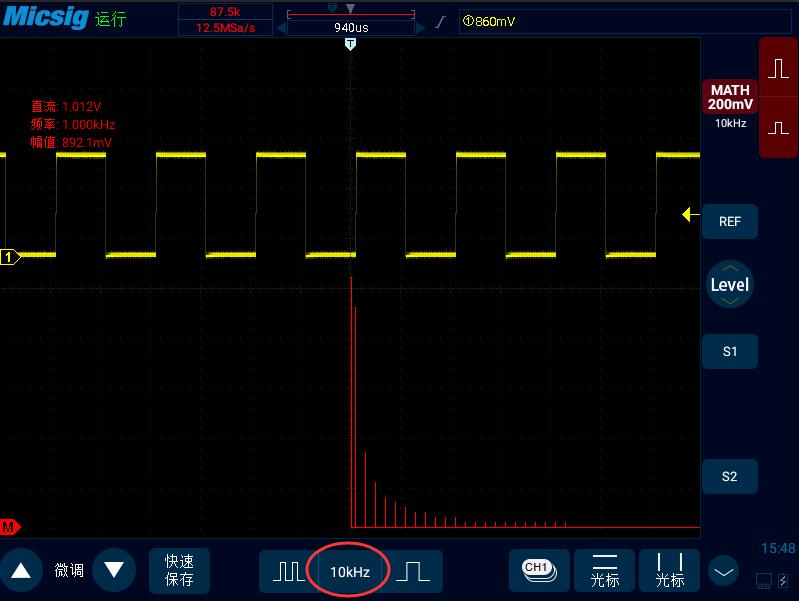
此時,橫坐標的時基變成了“頻基”,示波器橫坐標上一格代表10KHz
縱坐標依然還是代表電壓值。
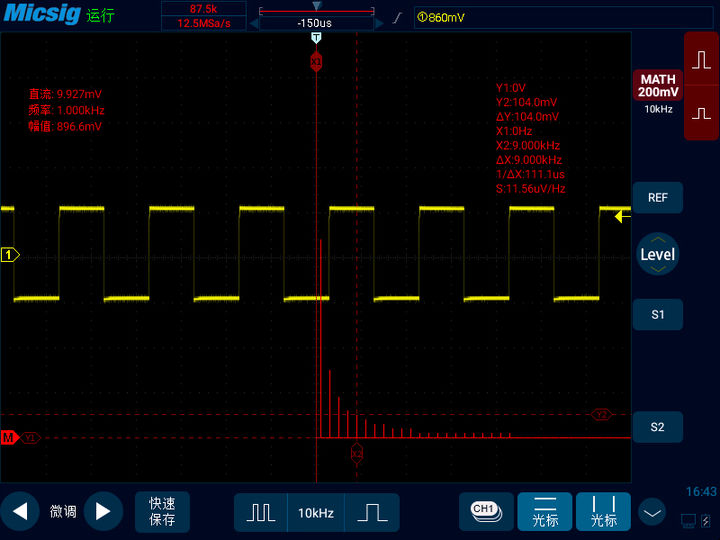
我們打開光標,通過微調,將X1調至0Hz,Y1調至0V,然后我們就可以通過移動X2和Y2來知道某個信號的頻率和電壓值了。也許你會奇怪,第一條直線0Hz是什么?其實那個就是信號中的直流成分,直流信號的頻率是0Hz。我們將通道的耦合方式改成交流,濾除直流信號,你就會發現第一條的直線消失了。
FFT快速傅立葉變換的作用:
FFT就是分析信號的頻譜,在物理學、電子類學科、數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學、海洋學、結構動力學等領域都有著廣泛的應用。
我們比較熟悉的廣播和電視,都需要調頻道來觀看聆聽不同的節目。而頻道,就是頻率的通道,不同的頻道就是將不同的頻率作為一個通道來進行信息傳輸。
示波器的頻域分析,在電源調試中也可以起到加速調試進程的作用。在計算機中,圖像、文件的壓縮也有用到傅立葉變換的計算。我們常用的PS軟件里也有很多工具運用到了傅立葉變換的算法。
再比如從某條曲線中去除一些特定的頻率成分,也就是濾波,是信號處理中十分重要的概念,也只有在頻域才能輕松的做到。我們用的降噪耳機,就是將外界嘈雜聲音的頻率過濾掉的原理。
-
示波器
+關注
關注
113文章
6282瀏覽量
185840
發布評論請先 登錄
相關推薦
傅立葉變換在機器學習中的應用 常見傅立葉變換的誤區解析
傅立葉變換與時域信號的關系 傅立葉變換在音頻信號處理中的應用
傅立葉變換與拉普拉斯變換的區別
傅立葉變換的基本概念 傅立葉變換在信號處理中的應用
經典傅里葉變換與快速傅里葉變換的區別
是否可以使用TLC320AIC3262片內miniDSP_A進行FFT變換對ADC采樣后的一組數據進行FFT?
使用MXO示波器的快速FFT功能進行EMI調試




 淺懂示波器FFT快速傅立葉變換功能及運用
淺懂示波器FFT快速傅立葉變換功能及運用










評論