離線式反激轉換器 (off-line flyback converter) 的反饋控制經常困擾著電源工程師,因為牽涉到連續導通模式 (continuous conduction mode, CCM) 與非連續導通模式(discontinuous conduction mode, DCM)的小信號模型、TL431與光耦合器(opto-coupler)的特殊反饋補償模式,使得反饋參數的設計,還流于試誤(cut and try)模式。本設計指南提供完整的理論設計,從功率級的轉換函數到設計TL431與光耦補償器,使得系統獲得良好的相位裕度(phase margin),達到瞬時穩定度的要求。本文將利用Mathcad 軟件做理論計算,同時以Simplis 模擬做比較驗證。
一、適用范圍 : 次級穩壓反激轉換器
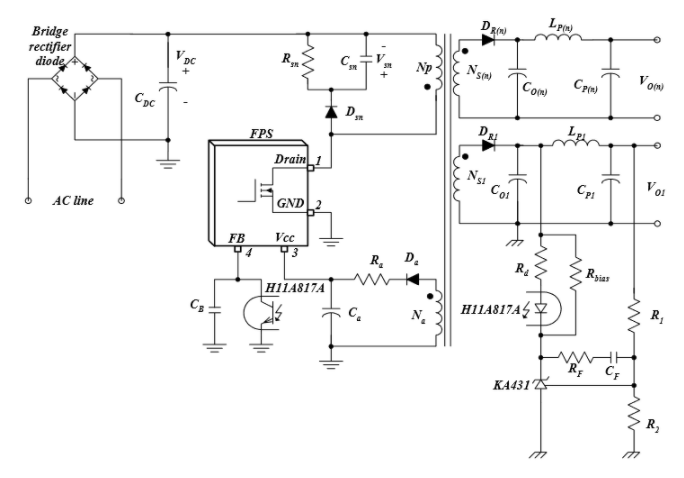
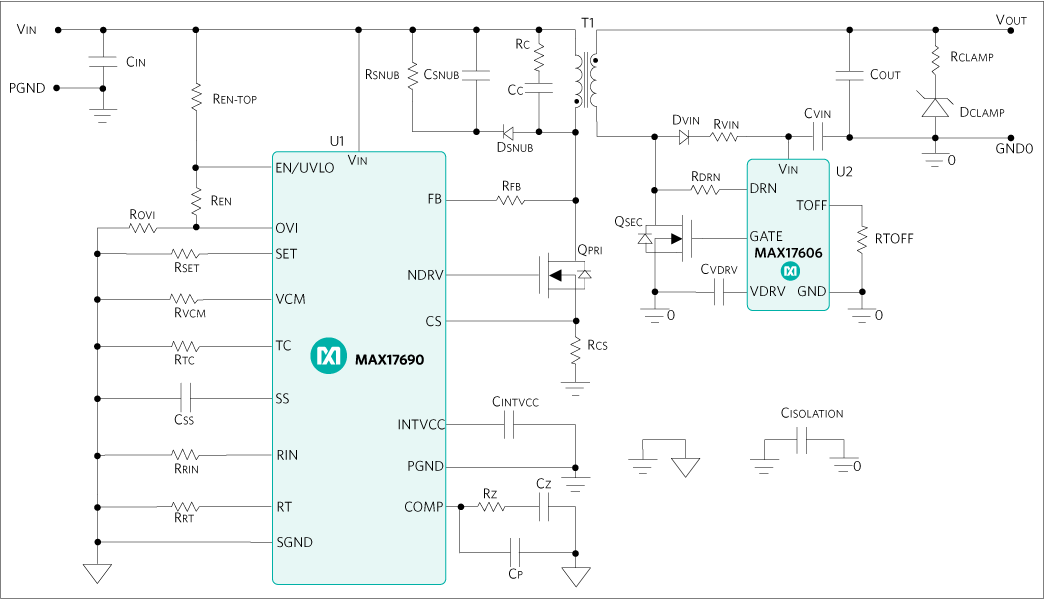
絕大部份反激轉換器都采用次級穩壓的峰值電流控制(peak current mode control)來完成調節輸出電壓的反饋方式,圖一為其簡圖。次級輸出電壓經過光耦與TL431電路,在初級側形成電壓VCOMP,這個電壓與初級峰值電流比較,決定開關晶體管Q的占空比,完成負反饋穩壓的作用。其中,RS 為初級電流檢測電阻,CTR 為光耦的電流傳遞比(current transfer ratio),GFB為小信號增益 (在RT773x IC內部設計為1/3),Se為消除次諧波振蕩(sub-harmonic oscillation) 所外加的斜率補償(slop compensation)。
為方便后續的推導與說明,電路做了基本的假設如下:
1.開關器件Q與次級二極管D為理想組件
2.變壓器視為理想器件
3.TL431的開回路增益為無限大 (常規的開路增益約50 ~ 60dB)
4.光耦的電流傳遞比為一常數
其中,光耦的電流傳遞比是一個極非線性的數值,隨著工作點(通過光耦二極管的電流)的變動,電流傳遞比也會隨著變化。但為了方便說明與推導起見,姑且將其視為定值。在常規的應用中,流過光耦二極管的電流很低,可能低于1mA,導致電流傳遞比可能小于20%。
其他名詞與符號定義如下:

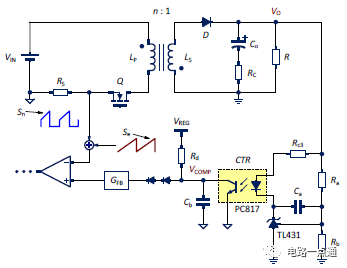
圖一、利用TL431與光耦反饋的反激轉換器
二、功率電路的小信號模型
在許多不同的參考文獻中可以找到不同的反激轉換器小信號模型[1-3],這些模型都是基于狀態平均(state averaging)法推導的,可能是因為簡化或假設條件不同而有些許差異。本文乃采用 Christophe Basso 的小信號模型作反饋補償設計[1]。從實用的角度而言,所有小信號模型都將得到近似的結果。
連續導通模式(CCM)的轉移函數(transfer function)

這是一個一個極點(pole)、兩個零點(zero)的系統,如圖二所示。極點的位置與電路參數以及負載輕重有關,而第一個零點為輸出電容與其等效串聯電阻(ESR)所構成,為一固定不動的零點。另一個零點在s-平面的右半邊,稱為右半平面零點(RHP zero),這個右半平面零點的位置與輸入電壓、負載電流的高低有關。在一個設計良好的系統里,交越頻率 (cross-over frequency) 必須設計得遠低于右半平面零點頻率,才能有足夠的相位裕量(phase margin)。所以在補償電路設計時,這個高頻的零點將忽略不計。
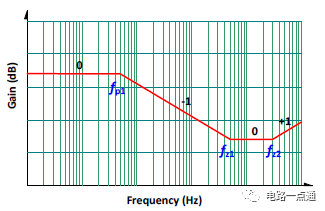 圖二、CCM 1P2Z 的轉移函數圖
圖二、CCM 1P2Z 的轉移函數圖
非連續導通模式 (DCM)的轉移函數

將(2)式的轉移函數繪制在波德圖(Bode Plot)上,如圖三。在DCM 模式下,功率電路小信號模型呈現兩極點與兩零點,不過其中有一個極點ωp2頻率極高(遠高于目標的交越頻率),在設計反饋時不需考慮。所以等效上,不論CCM 或是DCM,其功率級的轉移函數,均可視為一極點、兩零點(1P2Z)的形式,這非常有利于反饋組態電路的選定。從(1)與(2) 轉移函數來看,這些極點與零點,有些是固定不變的,如輸出電容等效串聯電阻ESR造成的零點。大部份的極零點與直流增益都與工作點(operating point)有關,所謂工作點即指某一個輸入電壓與某個負載電流工作條件。接下來,就用數值來說明這些極零點的變化。
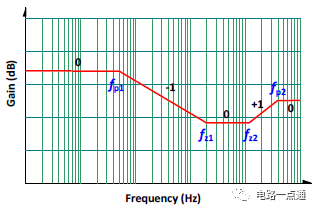
圖三、DCM 2P2Z 的轉移函數圖
工作點與極零點變化
舉一個常規的應用例子來說明:一個反激轉換器,輸入電壓范圍為90V 到360V,負載范為為0到3A,輸出電壓為12V。并有著下列的電路參數 : LP = 1.1mH, NP : NS = n = 7.7, CO = 1360μF, RESR = 30 mΩ, RS = 0.56Ω, fS = 65kHz, Se = 3.46 x 104 V/sec, GFB = 0.3333。(其中 Se 與GFB 必須由控制IC提供)根據反激轉換器的工作原理[4],在常規的設計里,高輸入電壓與輕載狀態總是讓轉換器傾向于非連續導通模式;反之,低輸入電壓與重載的條件下,轉換器會走向連續導通模式。其間存在著一條所謂 CCM與DCM 的邊界曲線,如圖四所示,在曲線上方為CCM 工作模式,曲線下方為DCM 工作模示。(3)式就是代表這條曲線的方程式。

圖四、CCM 與DCM 邊界曲線

不同工作點的零極點變化
表一為范例中的直流增益以及零極點位置的計算結果。圖五為輸入電壓與負載電流變化的波德示意圖。可以看出,當低輸入電壓與高負載時,增益曲線較低;反之,高輸入電壓與輕載時,增益曲線較高。這個事實關系到如何選擇工作點作為反饋設計的基準,很顯然,低輸入電壓與重載條件做為反饋設計點是比較恰當的。也就是說在這樣的條件下,如果擁有足夠的相位裕量,通常也能延伸到其他工作點有著更好的相對穩定裕量。
表一、不同工作點的直流增益與零極點位置
| VIN (V) | 90 | 180 | 270 | 360 | 90 | 90 | 90 | 360 | 360 | 360 |
| IO (A) | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 2.0 | 1.0 | 3.0 | 2.0 | 1.0 |
| Mode | CCM | CCM | CCM | DCM | CCM | CCM | DCM | DCM | DCM | DCM |
| G0 (dB) | 13.1 | 16.5 | 17.0 | 17.1 | 13.1 | 15.6 | 17.0 | 17.1 | 18.8 | 21.8 |
| fP1 (Hz) | 59.0 | 53.0 | 57.0 | 58.5 | 59.0 | 44.0 | 19.5 | 58.5 | 39.0 | 19.5 |
| fP2 (Hz) | NA | NA | NA | 21.7k | NA | NA | 25k | 21.7k | 32.6k | 65k |
| fZ1 (Hz) | 3.9k | 3.9k | 3.9k | 3.9k | 3.9k | 3.9k | 3.9k | 3.9k | 3.9k | 3.9k |
| fZ2 (Hz) | 16.5k | 44.2k | 75k | 106k | 16.5k | 24.7k | 49.5k | 106k | 160k | 319k |
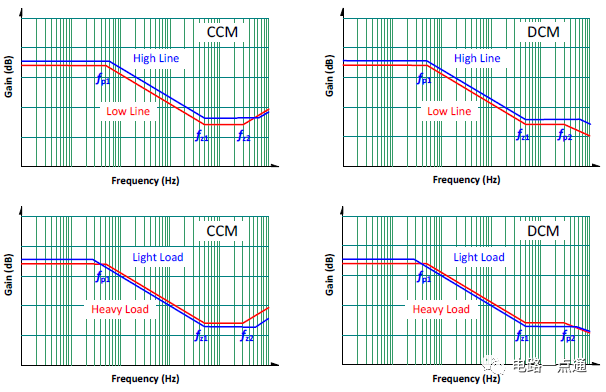
圖五、改變工作點的增益曲線變化
三、反饋補償電路設計
從前面的分析得知,不同的操作點有著不同的零極點位置以及不同的低頻直流增益,所以存在著許多設計補償電路的方法。基本上一個Type II 的補償器 (一個零頻率的極點,隨著一個低頻零點以及一個極點) 最適合做此類的補償。如果用一個低頻零點來補償功律電路的低頻極點,同時利用高頻極點來補償ESR零點,這樣將容易獲得較好的相位裕量。利用補償器的中頻段增益來設定適當的交越頻率,系統將有相當好的穩定度。
一種簡單實用的方法便是先設定好一個“目標回路增益”(target loop gain)為:

這樣的回路增益在波德圖上就是一條 -20dB/dec 斜率的直線,如圖六,在低頻直流部分有著極高(相當于補償器的開路增益)的增益,所以整個電路的直流穩態電壓調整率理論值可為零。同時,其交越頻率fC為

因為斜率近似 -20dB/dec,所以在交越頻率有著近90° 的相位裕量。對一個離線的反激轉換器而言,交越頻率設計在低壓輸入滿載時工作點為800Hz到3kHz為最恰當 (以65kHz 開關頻率而言)。
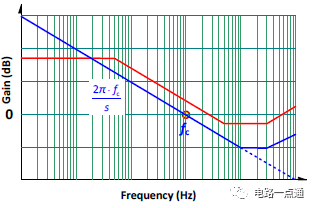
圖六、功率電路轉移函數曲線(紅色)與目標回路增益(藍色)
設計步驟
有了以上的了解與認知后,很自然的一般補償器設計的方法就可以應用了,現將這些步驟整理如下:
1.選擇低壓輸入與滿載做為補償電路設計基準的功率電路。如前所述,采用這個工作點設計的補償器可以延伸涵蓋到其他工作點,并且有更好的相位裕量。
2.設定交越頻率 fC,其回路增益波德圖為 -20dB/dec 斜率。越高的交越頻率,雖然代表著更快的瞬時響應,但是別忘了反激轉換器固有的右半平面零點問題,這個零點無法用傳統的極點補償,所以交越頻率必須遠低于這個零點位置。實務上,離線反激轉換器的交越頻率多半設計在3kHz以下。
3.定義一個兩極點、一零點的補償電路,并設定補償電路的零點為功率電路的低頻極點;設定補償電路的高頻極點為功率電路的ESR零點。利用一組Type II 的補償電路,恰可以結合功率電路的轉移函數,成為目標回路增益。
4.根據功率電路在fC 的增益,算出補償器的中頻增益。
5.同時,相位裕量可以先預估。
6.補償電路的轉換函數可以確定了:

也就是說 (6) 式的 A、ωcp1 與 ωcz1 都可以計算出來了。
補償電路的實現
1.選用最廣泛使用的TL431與光耦合器架構,如圖七。實現Type II 補償器的電路結構有許多種,不在此討論,僅提供最常用結合TL431與光耦的常規Type II電路計算與說明。
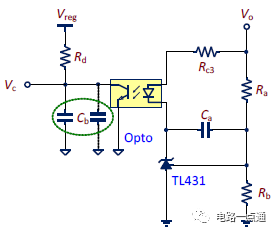
圖七、實現反饋補償的電路結構
2.圖七補償電路的小信號轉換函數如下 [5]
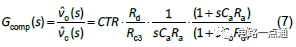
圖八為相應的補償器波德圖。
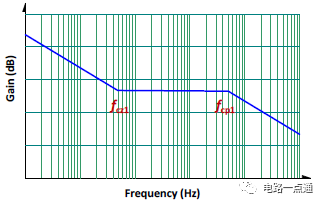
圖八、Type II 補償器波德圖
3.從(7)式看,共有Ra、Rb、Rc3、Rd、Ca、Cb 及 CTR 等七個參數待定。而已知的只有前面算出的三個關系式。



換句話說,有四個參數必須從其他條件獲得。
4.首先為電阻Rd,大部份新型的控制IC都已設定好,設計者可以從IC供貨商數據中獲得。
5.其次,TL431 的參考電壓也可從供貨商數據中得取,常規約為2.5V。為讓TL431正常運作,通過Rb 的電流(Ivd) 至少須125μA,一般加上余裕,可以設定成250μA。所以 Ra 與Rb 就可以很容易的計算出來。


6.此外,光耦的電流傳遞比(CTR)可以從供貨商數據里估計。事實上如前所述,CTR 為一非線性值,隨通過光耦二極管電流大小而變。一般通過光耦二極管電流約為幾百μA,CTR 約在0.1 到0.5之間,確實的數值必須透過精密量測而得。此例將假設CTR 為0.5。
7.如此一來,七個參數已經決定了四個,其余的三個參數可藉由(8)、(9)及(10)三個關系式算出唯一解。
8.算出RC3 的數值后必須要檢討一下。從TL431 運行原理,其陰極電壓必須高于2.5V,同時流過陰極的電流必須大于1mA 才可以獲得正確的穩壓。通常會在光耦二極管上并聯一個1kΩ 左右的電阻以提供足夠的陰極電流。特別注意,這個并聯電阻并不會改變系統小信號特性。所以可以得到下列關系式:
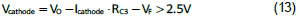

其中VF 為光耦二極管的順向壓降,常規約略為1.0V。RC3的最大值就可以估計出來了。

代入前面的例子,同時假定最大陰極電流為1.5mA,則RC3必須小于5.6kΩ。太高的RC3會降低補償電路的中頻增益。如果計算出來的RC3大于上限值就表示必須降低設定交越頻率,或采用其他的補償計算方法。
9.光耦合器在先天上存在一個并聯于光耦三極管的等效電容,必須用電路量測的方法測得,常規約在2nF到5nF之間。補償器計算出來的Cb值必須減去這個雜散電容,才是要外加的電容值。如果算出來的Cb值比雜散電容小,那就不需要外加電容了,不過因為不能完全補償ESR零點(極點靠近低頻),所以相位裕量會變差一些。
設計工具與模擬驗證
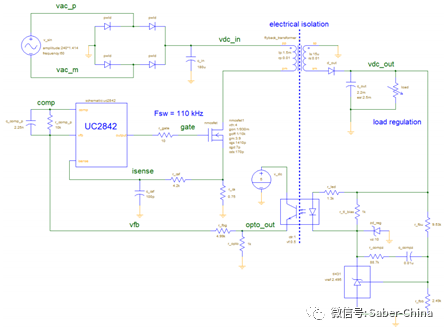
為了讓上述計算可以快速進行,特別制作兩個Mathcad計算程序“Flyback CCM Type II Compensation” 與 “Flyback Loop Gain Analysis”,方便反饋的計算與分析。同時可藉由Simplis仿真來比較本文模型計算的誤差。圖九為Simplis仿真電路圖,圖十到圖十二為本文提供的設計方法用Mathcad 分析計算與Simplis 模擬結果比較。圖十為功率電路轉移函數波德圖,圖十一為補償器電路轉移函數波德圖,圖十二為回路增益波德圖。(a)為幅值,(b)為相位。圖中紅色實曲線為Mathcad依據小信號模型計算結果,藍色虛曲線為用Simplis直接仿真的結果。可以看出從低頻段到交越頻率,小信號模型有很好的準確度。高頻部份由于小信號模型的誤差,有比較大的誤差,不過因為回路增益已遠小于1,對于實際瞬時響應影響不大。圖十三為用Simplis仿真在輸入電壓為90V情況下階梯負載變化(負載自1A瞬變到3A)的輸出電壓瞬時響應圖,可以看出只有很小的過沖(overshoot)以及很快的回復時間(settling time)。
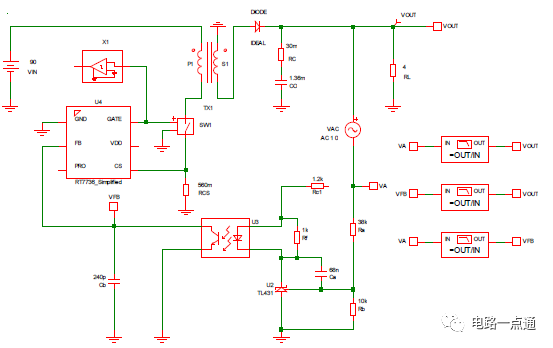
圖九、Simplis 仿真電路圖
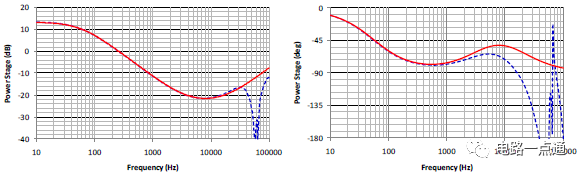
圖十、功率電路轉移函數波德圖 (a) 幅值, (b) 相位
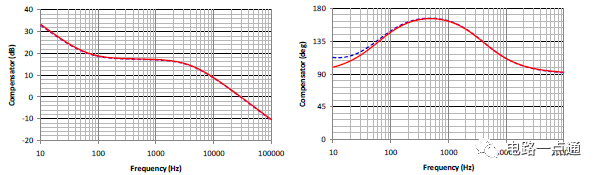
圖十一、補償器電路轉移函數波德圖 (a) 幅值, (b) 相位
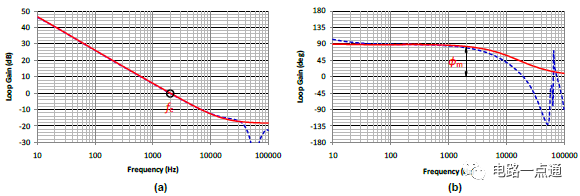
圖十二、回路增益波德圖 (a) 幅值, (b) 相位
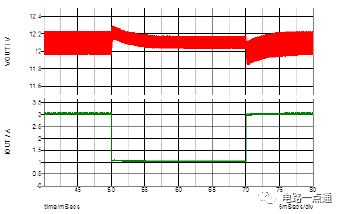
圖十三、負載瞬變瞬態響應圖
-
二極管
+關注
關注
147文章
9702瀏覽量
167554 -
轉換器
+關注
關注
27文章
8743瀏覽量
148032 -
光耦合器
+關注
關注
8文章
498瀏覽量
36309 -
TL431
+關注
關注
19文章
289瀏覽量
80943 -
光耦
+關注
關注
30文章
1451瀏覽量
57930
原文標題:設計指南:離線反激式轉換器的反饋控制
文章出處:【微信號:電路一點通,微信公眾號:電路一點通】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 離線反激式轉換器的反饋控制設計指南
離線反激式轉換器的反饋控制設計指南











評論