Sadaf Saleem| 作者

羅伯特|編輯

神經網絡是深度學習算法的基本構建模塊。神經網絡是一種機器學習算法，旨在模擬人腦的行為。它由相互連接的節點組成，也稱為人工神經元，這些節點組織成層次結構。

神經網絡與機器學習有何不同？

神經網絡是一種機器學習算法，但它們與傳統機器學習在幾個關鍵方面有所不同。最重要的是，神經網絡可以自行學習和改進，無需人的干預。它可以直接從數據中學習特征，因此更適合處理大型數據集。然而，在傳統機器學習中，特征需要手動提供。

為什么使用深度學習？

深度學習的一個關鍵優勢是其處理大數據的能力。隨著數據量的增加，傳統機器學習技術在性能和準確性方面可能變得低效。而深度學習則能夠持續表現出色，因此是處理數據密集型應用的理想選擇。

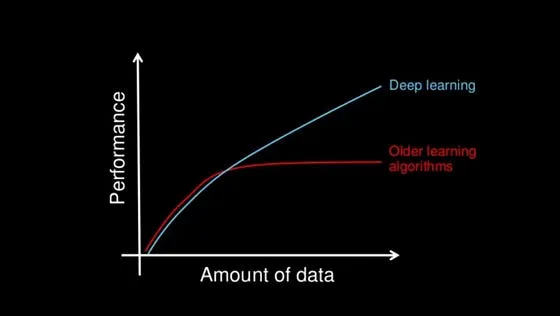
有人會問，為什么我們要費心研究深度學習的結構，而不是簡單地依賴計算機為我們生成輸出結果，這是一個合理的問題。然而，深入了解深度學習的底層結構可以帶來更好的結果，這其中有很多令人信服的理由。

研究深度學習結構的好處是什么？

通過分析神經網絡的結構，我們可以找到優化性能的方法。例如，我們可以調整層數或節點的數量，或者調整網絡處理輸入數據的方式。我們還可以開發更適合分析醫學圖像或預測股市的神經網絡。如果我們知道網絡中的哪些節點對于特定輸入被激活，我們可以更好地理解網絡是如何做出決策或預測的。

神經網絡如何工作？

每個神經元代表一個計算單元，接收一組輸入，執行一系列計算，并產生一個輸出，該輸出傳遞給下一層。

就像我們大腦中的神經元一樣，神經網絡中的每個節點都接收輸入，處理它，并將輸出傳遞給下一個節點。隨著數據在網絡中傳遞，節點之間的連接會根據數據中的模式而加強或減弱。這使得網絡可以從數據中學習，并根據其學到的知識進行預測或決策。

想象一個28x28的網格，其中某些像素比其他像素更暗。通過識別較亮的像素，我們可以解讀出在網格上寫的數字。這個網格作為神經網絡的輸入。

網格的行排列成水平的一維數組，然后轉化為垂直數組，形成第一層神經元，就像這樣；

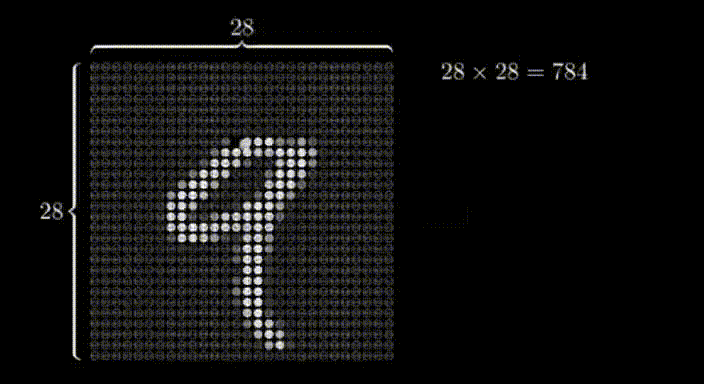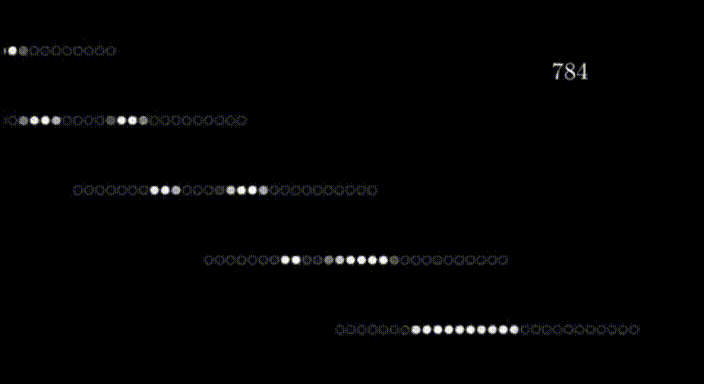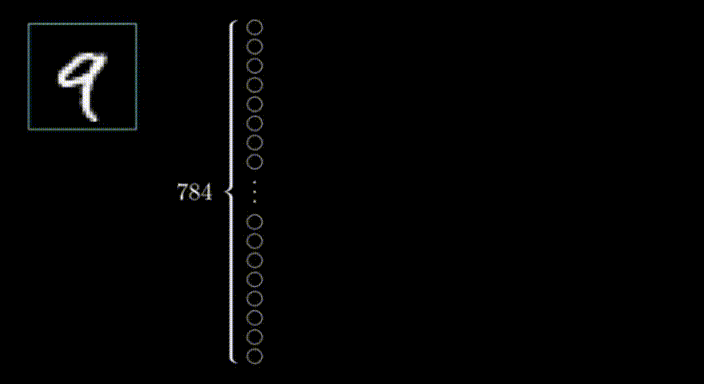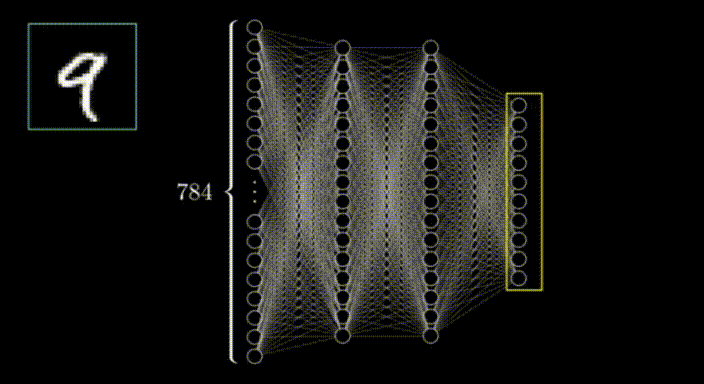
在第一層的情況下，每個神經元對應于輸入圖像中的一個像素，每個神經元內的值代表該像素的激活或強度。神經網絡的輸入層負責接收原始數據（在本例中是圖像）并將其轉化為可以被網絡其余部分處理的格式。

在這種情況下，我們有28x28個輸入像素，這給了我們784個輸入層的神經元。每個神經元的激活值要么是0，要么是1，這取決于輸入圖像中相應的像素是黑色還是白色。

神經網絡的輸出層在這種情況下包括10個神經元，每個代表一個可能的輸出類別（在本例中是數字0到9）。輸出層中每個神經元的輸出代表輸入圖像屬于該特定類別的概率。最高概率值確定了對于該輸入圖像的預測類別。

隱藏層

在輸入層和輸出層之間，我們有一個或多個隱藏層，對輸入數據執行一系列非線性變換。這些隱藏層的目的是從輸入數據中提取對當前任務更有意義的高級特征。您可以決定在網絡中添加多少隱藏層。

隱藏層中的每個神經元都從前一層的所有神經元接收輸入，并在將結果通過非線性激活函數之前，對這些輸入應用一組權重和偏差。這個過程在隱藏層的所有神經元上重復，直到達到輸出層。

前向傳播

前向傳播是將輸入數據通過神經網絡生成輸出的過程。它涉及計算網絡每一層中每個神經元的輸出，通過將權重和偏差應用于輸入并通過激活函數傳遞結果來完成。

數學公式：或 其中， 是神經網絡的輸出， 是非線性激活函數，是第 個輸入特征或輸入變量， 是與第個輸入特征或變量相關聯的權重， 是偏差項，它是一個常數值，加到輸入的線性組合上。 ：這是輸入特征和它們相關權重的線性組合。有時這個術語也被稱為輸入的“加權和”。

反向傳播

反向傳播是訓練神經網絡中常用的算法。它涉及計算梯度，即損失函數相對于網絡中每個權重的變化的度量。損失函數衡量了神經網絡在給定輸入下能夠正確預測輸出的能力。通過計算損失函數的梯度，反向傳播允許神經網絡以減小訓練過程中的整體誤差或損失的方式更新其權重。

該算法通過將來自輸出層的誤差沿著網絡的層傳播回去，使用微積分的鏈式法則計算損失函數相對于每個權重的梯度。然后，這個梯度用于梯度下降優化，以更新權重并最小化損失函數。

神經網絡中使用的術語

神經網絡的訓練是根據輸入數據和期望輸出來調整神經網絡權重的過程，以提高網絡預測的準確性。權重：權重是在訓練過程中學到的參數，它們決定了神經元之間連接的強度。每個神經元之間的連接被分配一個權重，該權重與輸入值相乘，以確定其輸出。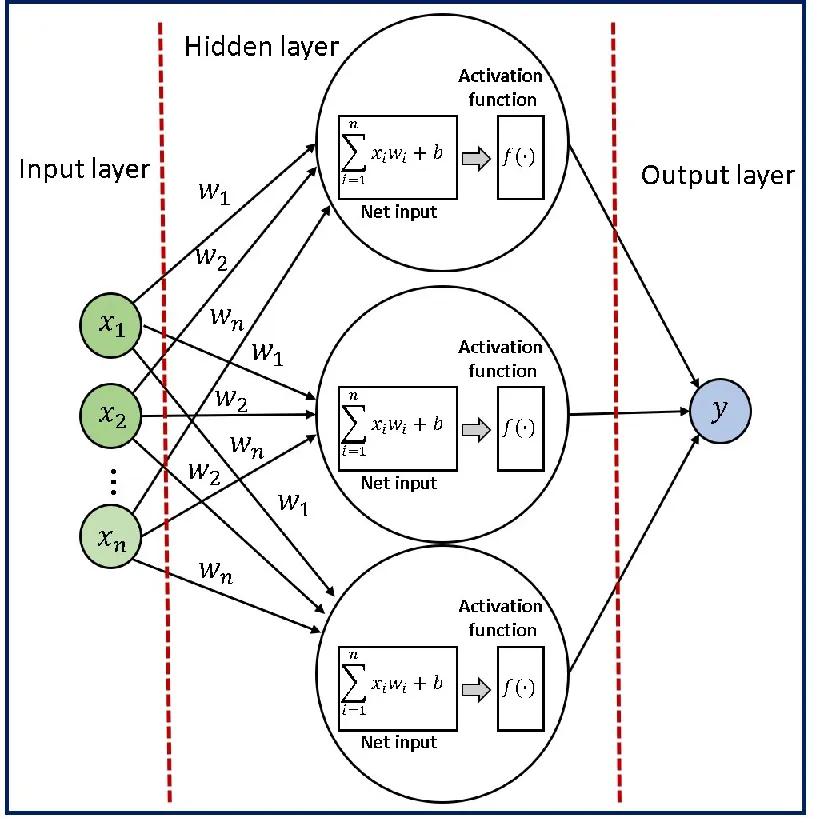

偏差（Bias）：偏差是另一個在給定層中神經元的加權和上添加的學習參數。它是神經元的附加輸入，有助于調整激活函數的輸出。

非線性激活函數（Non-linear activation function）：非線性激活函數應用于神經元的輸出，引入了網絡中的非線性。非線性很重要，因為它允許網絡建模輸入和輸出之間的復雜、非線性關系。在神經網絡中常用的激活函數包括 Sigmoid 函數、ReLU（修正線性單元）函數和 softmax 函數。損失函數（Loss function）：這是一個數學函數，用于衡量神經網絡的預測輸出與真實輸出之間的誤差或差異。經驗損失度量了整個數據集上的總損失。交叉熵損失常用于輸出概率在0和1之間的模型，而均方誤差損失用于輸出連續實數的回歸模型。目標是在訓練過程中最小化損失函數，以提高網絡預測的準確性。損失優化（Loss optimization）：這是在神經網絡進行預測時，最小化神經網絡所產生的誤差或損失的過程。這是通過調整網絡的權重來完成的。

梯度下降（Gradient descent）：這是一種用于尋找函數最小值的優化算法，例如神經網絡的損失函數。它涉及迭代地調整權重，沿著損失函數的負梯度方向。其思想是不斷將權重朝著減小損失的方向移動，直到達到最小值。

讓我們通過實際例子記住這些術語：

1. 想象一家公司希望通過銷售產品來最大化利潤。他們可能有一個基于各種因素如價格、營銷支出等來預測利潤的模型。偏差可能指的是影響產品利潤但與價格或營銷支出無直接關系的任何固定因素。例如，如果產品是季節性物品，可能在一年中的某些時段存在對更高利潤的偏差。實際利潤與預測利潤之間的差異就是損失函數。梯度下降涉及計算損失函數相對于每個輸入特征的梯度，并使用這個梯度迭代地調整特征值，直到找到最佳值的過程，而涉及找到最小化損失函數的輸入特征的最佳值的過程就是損失優化。利潤預測模型可能會使用非線性激活函數將輸入特征（例如價格、營銷支出）轉化為預測的利潤值。這個函數可以用來引入輸入特征和輸出利潤之間的非線性關系。2. 想象你正在玩一個視頻游戲，你是一個角色試圖到達一個目的地，但你只能在二維平面上移動（前后和左右）。你知道目的地的確切坐標，但不知道如何到達那里。你的目標是找到到達目的地的最短路徑。在這種情況下，損失函數可以是你當前位置與目的地之間的距離。損失函數的梯度將是通往目的地最陡坡度的方向和大小，你可以使用它來調整你的移動，靠近目的地。隨著你靠近目的地，損失函數減小（因為你離目標更近了），梯度也相應改變。通過反復使用梯度來調整你的移動，最終你可以以最短路徑到達目的地。希望你在了解神經網絡方面有了更深入的了解。為了更好地理解這一概念，請參考文章中提到的視頻。