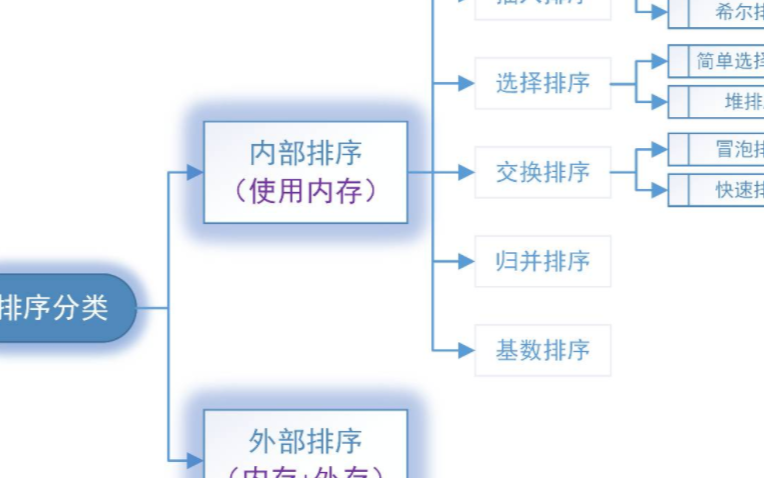
選擇排序： （Selection sort）是一種簡單直觀的排序算法，也是一種不穩定的排序方法。

選擇排序的原理：

一組無序待排數組，做升序排序，我們先假定第一個位置上的數據就是最小的，我們用一個參數記錄這個最小的數，然后依次把后面的每個位置的數據和這個最小的比較，如果比這個數小就替換兩個位置數據，等到第一輪比較完成就能確定最小的數據排在第一位了，然后第二輪從第二個位置開始，相同的方式比較，每次都能找到本輪最小的值，直至全部待排元素個數為0的時候，數組就排好順序了。

選擇排序流程圖

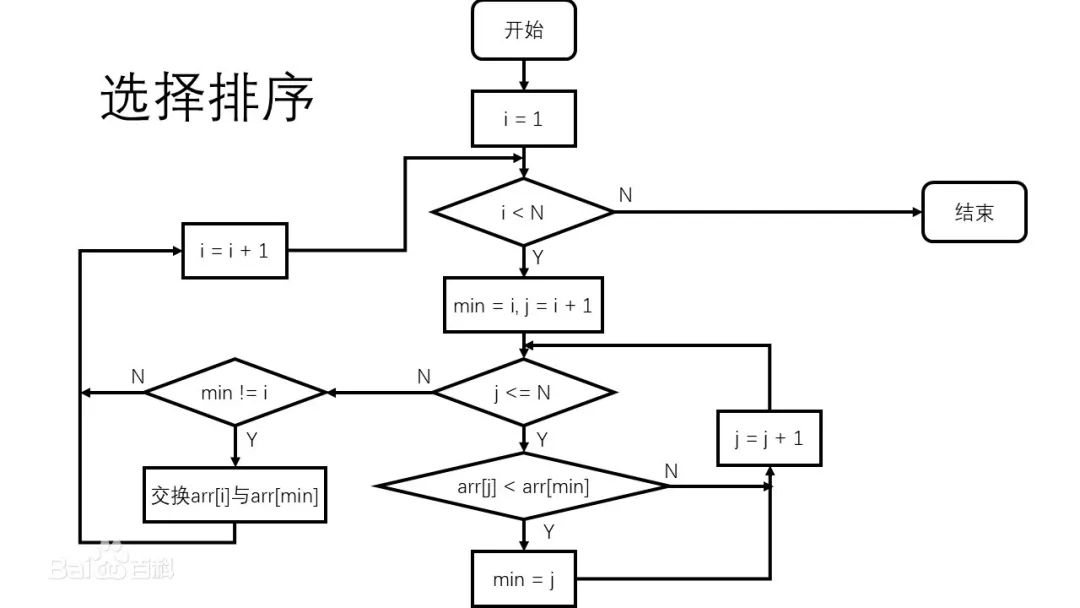
我們來進行詳細解析看看

首先我們給個無序數組[4,6,15,9,12,3,32]進行升序排序，因為需要確定每個數組的長度，所以需要比較數組長度-1輪，當前面的元素都排好了之后，那么數組最后一個元素自然就確定了位置。

我們定義兩個值，minIndex，minNum用來分別表示每一輪的找到的最小值的下標和值，后面未排序的值都和minNum比較，從而找出每一輪的最小值。

• 第一輪我們以下標為1的第一位作為標志位（也就是把第一個值當做最小值），那么此時minIndex=0，minNum=4，經過和 minNum 比較發現后面只有3比4小，那么3和4交換位置，minIndex=5，minNum=3，把4換到下標為5的位置，如下圖所示：

第一輪我們得到的結果是[3,6,15,9,12,4,32]，本輪最小數是：3，所以3放到本輪標志位，也就是第一位

• 第二輪：拿到第一輪排序的值作為初始值[3,6,15,9,12,4,32]，同第一輪一樣，此時6作為標志位minNum=6，minNum和其他比較，只有4比6小，需要交換位置，如下圖所示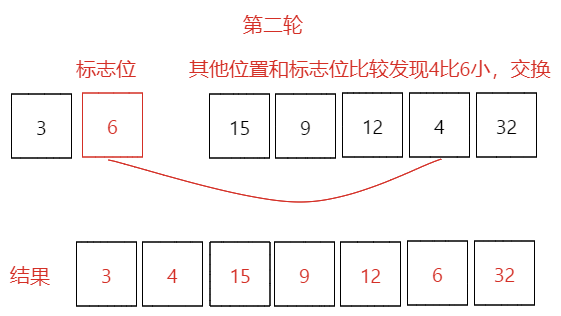第二輪排序結果[3,4,15,9,12,6,32]，本輪最小數是：4
• 第三輪：初始值[3,4,15,9,12,6,32],這次標志位15，minNum=15，minIndex=2，minNum先比和9比較，發現9比15小，minNum=9，minIndex=3，然后minNum和12比較，不需要替換minNum，再和6比較，minNum=6，minIndex=5,后面再比較已經沒有比6小了，那么本輪就是初始標志位15和下標為5，值為6的數據換位置。
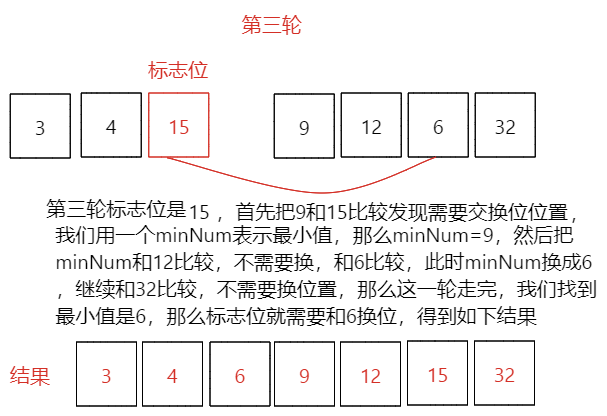
  第三輪排序結果[3,4,6,9,12,15,32]，本輪最小數是：6
• 第四、五、六輪：初始值[3,4,6,9,12,15,32]，經過前面的比較我們可以看到數組已經排序完成，但是程序并不知道，會繼續比較下去，把下標為4、5、6位置都作為標志位比較一次，發現都不需要變動位置，那么最終執行完成之后就能排序完成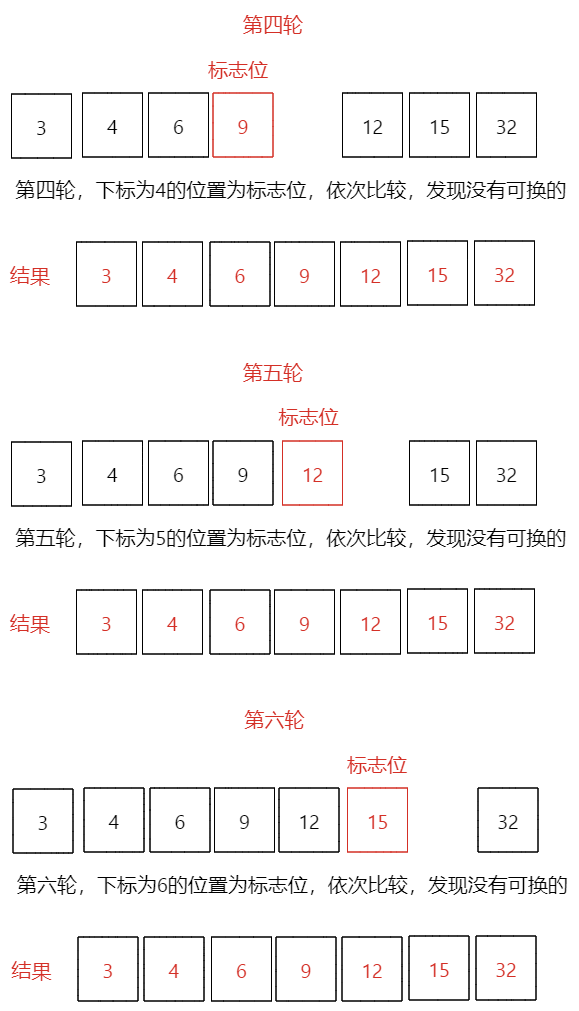第四、五、六輪排序結果[3,4,6,9,12,15,32]

到這，我們已經清楚了每個步驟做了什么，那么接下來上代碼驗證一下：

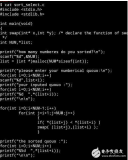
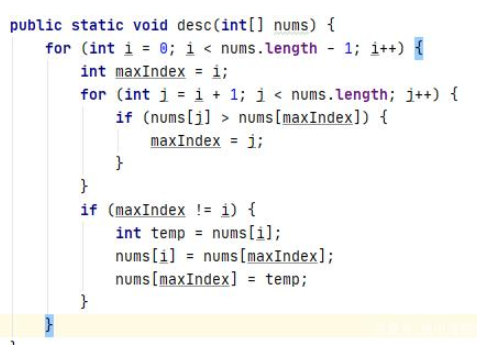
Java代碼實現

public class selectionSort {
     public static void main(String[] args){
          int[] arr = new int[]{4,6,15,9,12,3,32};
         for(int i=0;i< arr.length-1;i++){//每次循環都會找出最小的數
             //記錄最小數的下標
             int minIndex = i;
             //記錄最小數
             int minNum = arr[i];
             //每次循環都會找出最小的數
             for(int j=i+1;j< arr.length;j++){
                 if(arr[j]< minNum){//如果當前數比最小數小，則更新最小數
                     minNum = arr[j];//更新最小數
                     minIndex = j;//更新最小數的下標
                 }
             }
             //將最開始假定的小的數移動到真實最小的位置
             arr[minIndex]=arr[i];
             arr[i]=minNum;//將標志位放到最小數原來所在的位置
             
             //打印結果，方便查看
             System.out.print("第"+(i+1)+"輪[");
             for(int a=0;a< arr.length;a++){
                 System.out.print(arr[a]+"t");
             }
             System.out.println ("]，本輪最小數是："+minNum);
         }
         System.out.print("最終結果[");
         for(int i=0;i< arr.length;i++){
             System.out.print(arr[i]+"t");
         }
         System.out.println("]");
     }
 }

輸出結果

第1輪[3 6 15 9 12 4 32 ]，本輪最小數是：3
  第2輪[3 4 15 9 12 6 32 ]，本輪最小數是：4
  第3輪[3 4 6 9 12 15 32 ]，本輪最小數是：6
  第4輪[3 4 6 9 12 15 32 ]，本輪最小數是：9
  第5輪[3 4 6 9 12 15 32 ]，本輪最小數是：12
  第6輪[3 4 6 9 12 15 32 ]，本輪最小數是：15
  最終結果[3 4 6 9 12 15 32 ]

時間復雜度

我們通過上面的細節拆分發現，無論是否是已經排好的還是沒排好的情況，我們都需要每個數字都比較到，那么就出現N個元素的數組，第一輪是n次比較，第二輪是從第二個位置開始，那么就是n-1，第三輪就是n-2次... 最后是1，那么就出現了n+(n-1)+(n-2)+(n-3)...1,這是一個等差數列，求和為一個二次型多項式，因為等差數列求和會出現二次型；我們取最高階就是n^2,所以時間復雜度就是O(n^2),而且最好和最壞的情況時間復雜度都是O(n^2)