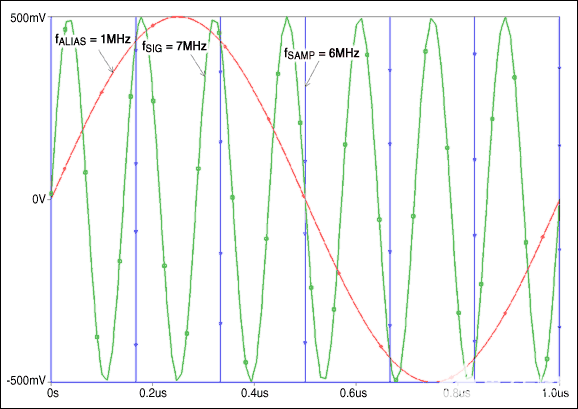
我們以示波器為例，看看頻域中的尼奎斯特頻率和混疊現象。

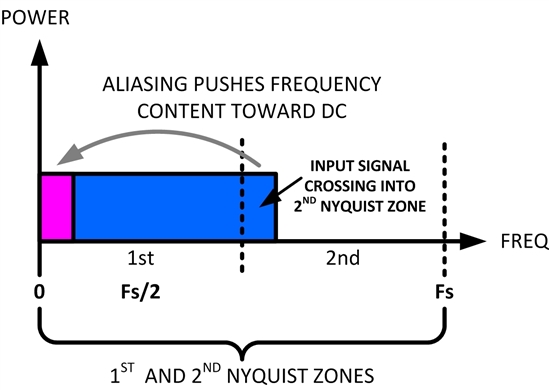
尼奎斯特頻率是任何實時數字化示波器可進行采集而不會混疊的最高頻率。此頻率為采樣率的一半。超過尼奎斯特頻率的頻率將會導致采樣不足，從而出現混疊。尼奎斯特頻率也稱為折疊頻率，因為在查看頻域時，混疊的頻率分量將從該頻率向后折疊。

信號中的頻率分量高于采樣率的一半時發生混疊。因為 FFT 頻譜受到該頻率的限制，所以任何較高的分量都以較低（混疊）的頻率顯示。

下圖對混疊做了說明。這是 990 Hz 方波的頻譜，具有很多的諧波。方波的水平時間 /格設置可設置采樣率，從而導致 FFT 分辨率為 1.91 Hz。從顯示的 FFT頻譜波形中可看到，高于尼奎斯特頻率的輸入信號分量要在顯示中鏡像（混疊），并反映在右邊沿之外。

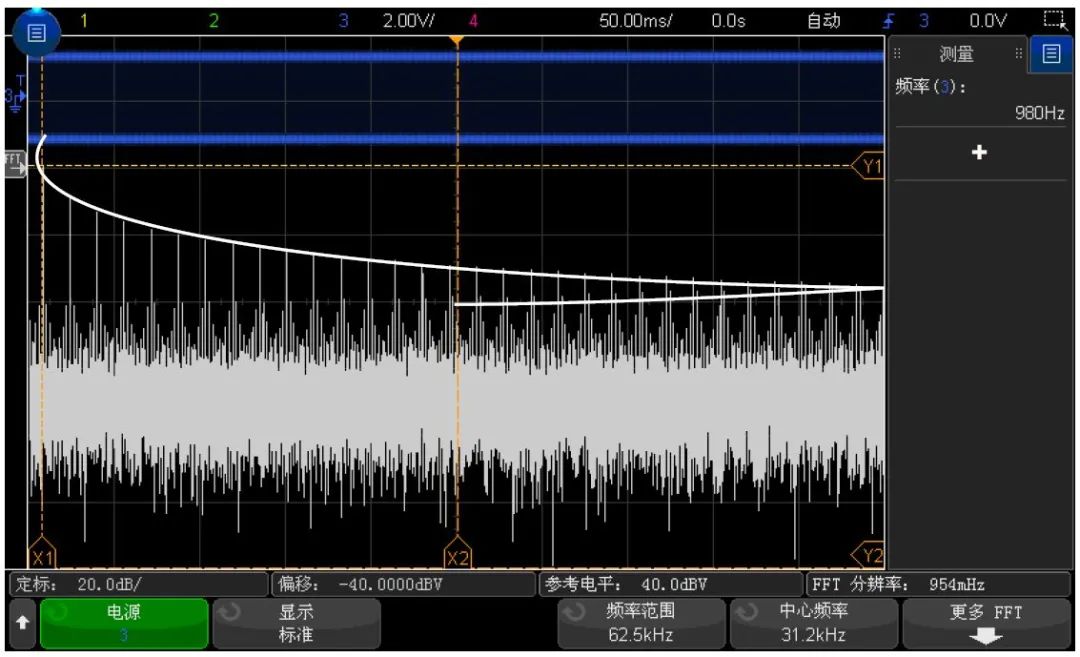
混疊

因為頻率范圍為從約等于 0 到尼奎斯特頻率，所以防止混疊的最佳方式是確保頻率范圍大于輸入信號中出現的高能量頻率。

Nyquist 采樣定理

數字測量應用所需的采用率為多少？一些工程師對于 Nyquist 理論深信不疑，并且認為只要采樣率是示波器帶寬的 2 倍便足矣。而其他工程師則不相信建立于 Nyquist 標準的數字濾波技術，更愿意使用采樣率為帶寬技術指標 10 至 20 倍的示波器。實際情況介于二者之間。

若要理解其中的原因，則必須了解 Nyquist 的理論及其與示波器頻率響應之間的關系。Harry Nyquist 博士假設：Nyquist 采樣定理對于具有最大頻率 fMAX 的有限帶寬信號，等間隔采樣頻率 fS 必須大于兩倍的最大頻率 fMAX，才能唯一地重建信號而不會有混疊現象。

Nyquist 采樣定理可以歸納為兩個簡單規則，然而，對于 DSO 技術而言卻不是那么簡單。

1. 采集的最高頻率分量必須小于采樣率的一半。

2. 第二個規則是必須等間隔采樣，而這一點經常會被遺忘。

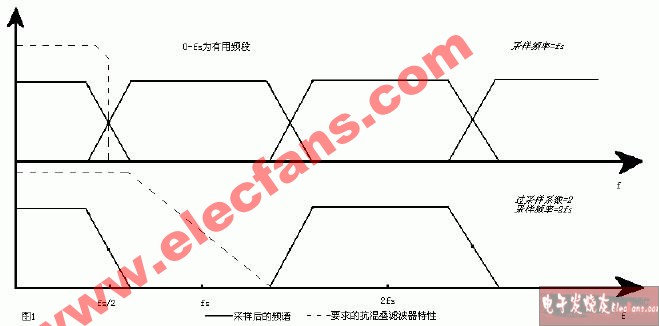
Nyquist 所稱的 fMAX 就是我們通常所指的 Nyquist 頻率（fN），它不同于示波器帶寬（fBW）。如果示波器帶寬恰好指定為 Nyquist（fN），則意味著示波器具有理想的磚墻式（brick-wall）響應，該響應在此相同頻率下會完全衰減（如圖 2 所示）。低于 Nyquist 頻率的頻率分量會完全通過（增益 =1），高于 Nyquist 頻率的頻率分量則會完全予以排除。然而，這種頻率響應濾波器無法在硬件中實施。

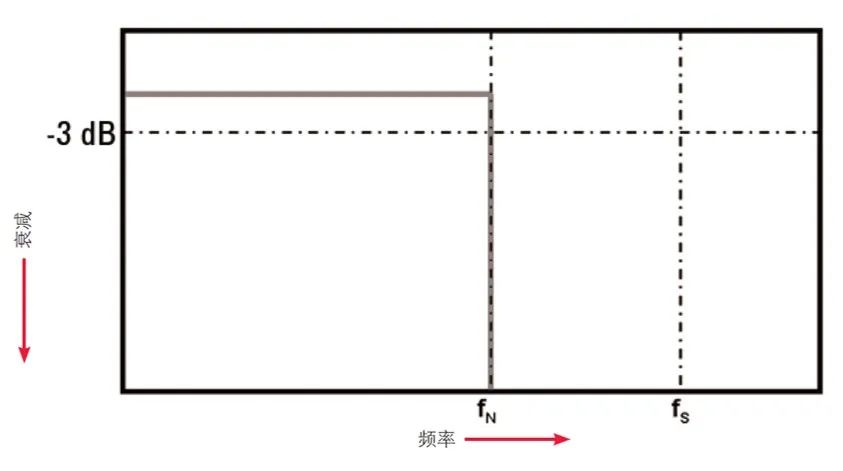
圖 2：理想的磚墻式頻率響應

帶寬技術指標為 1 GHz 及以下的大部分示波器具有稱為高斯頻率響應的響應類型。當信號輸入頻率接近示波器的指定帶寬時，測得的幅度會慢慢下降。信號在帶寬頻率下將會衰減 3 dB（~30%）。如果示波器的帶寬正好指定為 Nyquist（fN）（如圖 3 所示），輸入信號超過這個頻率的分量盡管衰減超過 3 dB，但也被采樣（紅色陰影部分），尤其當輸入信號中包含快速邊沿時，情況更是如此（測量數字信號時）。這種現象違背了 Nyquist 采樣定理的第一條規則。

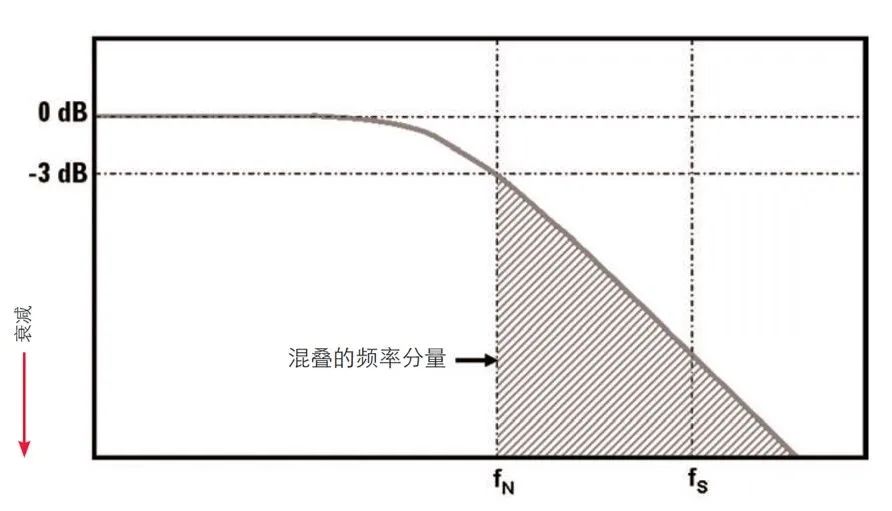
圖 3：帶寬（fBW）指定為 Nyquist 頻率（fN）時，典型的示波器高斯頻率響應

大多數示波器廠商不會將示波器的帶寬指定在 Nyquist 頻率（fN），不過也有部分廠商會這樣做。但是，波形記錄儀 / 數字轉換器的廠商往往會將其儀器的帶寬指定在 Nyquist 頻率。現在我們看一下，如果示波器的帶寬與 Nyquist 頻率（fN）相同時會是什么狀況。

圖 4 顯示：在三或四通道模式下工作時， 500-MHz 帶寬的示波器正好以 1 GSa/s的速度進行采樣。盡管輸入信號的基本頻率（時鐘頻率）處于 Nyquist 的范圍內，但是信號邊沿所包含的重要頻率分量遠落在 Nyquist 頻率（fN）之外。仔細查看會發現，該信號的邊沿具有不同程度的預沖、過沖和各種邊沿速度，呈現出“不穩定” 的趨勢。這就是混疊的跡象，它清晰地表明僅僅使用帶寬為采樣率 2 倍的示波器還不足以獲得可靠的數字信號測量結果。

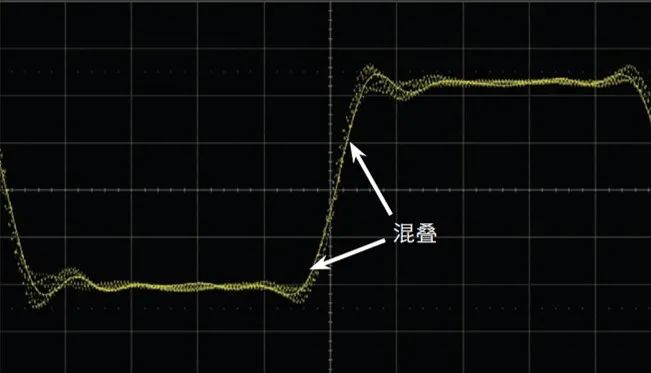
圖 4：使用 1 GSa/s 采樣率和 500-MHz 帶寬的示波器進行采樣所產生的混疊邊沿

那么，示波器的帶寬（fBW）的定義應該怎么關聯到波器的采樣率（fS）和 Nyquist 頻率（fN）呢？為了盡量避免對超出 Nyquist 頻率（fN）的頻率分量進行采集，大多數示波器廠商將其具有典型高斯頻率響應的示波器帶寬指定為實時采樣率的 1/4 至 1/5 或更低（如圖 5 所示）。盡管以比示波器帶寬大更多倍的速率采樣可以進一步降低采集 Nyquist 頻率（fN）之外頻率分量的可能性，但是 4:1 的采樣率與帶寬比足以獲得可靠的數字測量結果。

帶寬技術指標在 2-GHz 和更高范圍的示波器通常具有更陡峭的頻率衰減響應 / 特征。我們將這種類型的頻率響應稱為“最大平坦度”響應。由于具有最大平坦度響應的示波器接近于磚墻式濾波器的理想特征，在這種情況下，超出 Nyquist 的頻率分量衰減程度更高，因此無需進行多次采樣即可很好地顯示使用數字濾波的輸入信號。理論上廠商可以將具有此類響應的示波器帶寬（假設前端模擬硬件具備相應能力）指定為 fS/2.5。

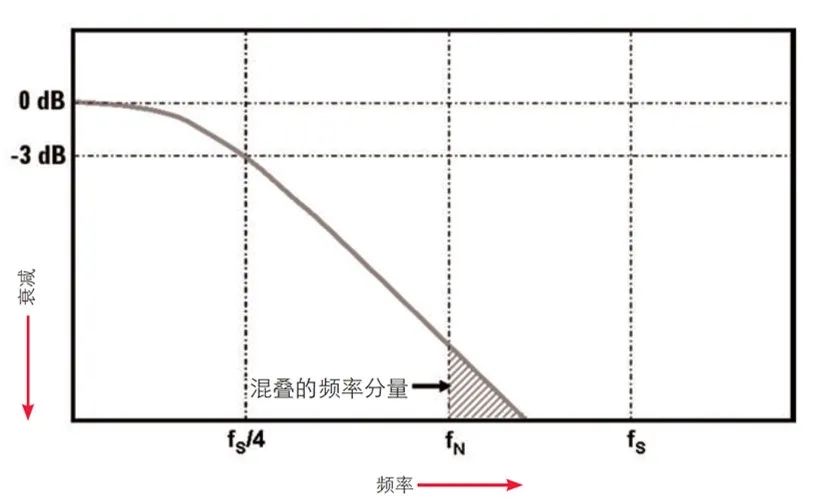
圖 5：將示波器帶寬（fBW）限制為采樣率的 1/4（fS/4），可以降低 Nyquist 頻率（fN）之上的頻率分量

圖 6 顯示了 500-MHz 帶寬的示波器捕獲邊沿速度在 1 ns（10% - 90%）范圍的 100-MHz 的時鐘信號。500 MHz 的帶寬技術指標是精確捕獲此數字信號的最小推薦帶寬。這一特定的示波器能夠在雙通道工作模式下以 4 GSa/s 進行采樣，或者在三或四通道工作模式下以 2 GSa/s 進行采樣。圖 6 顯示的是 2 GSa/s 采樣的示波器，其采樣頻率是 Nyquist 頻率（fN）的兩倍，帶寬頻率（fBW）的四倍。該圖表明，采樣率與帶寬之比為 4:1 的示波器可以非常穩定而準確地表示輸入信號。并且，借助 Sin(x)/x 波形重建 / 插值數字濾波技術，此示波器的波形和測量分辨率可達幾十皮秒的量級。與我們之前圖 4 所顯示的例子（采用相同帶寬的示波器，但僅為帶寬（fN）兩倍的速度進行采樣）相比，波形穩定性和精確度的差別顯而易見。

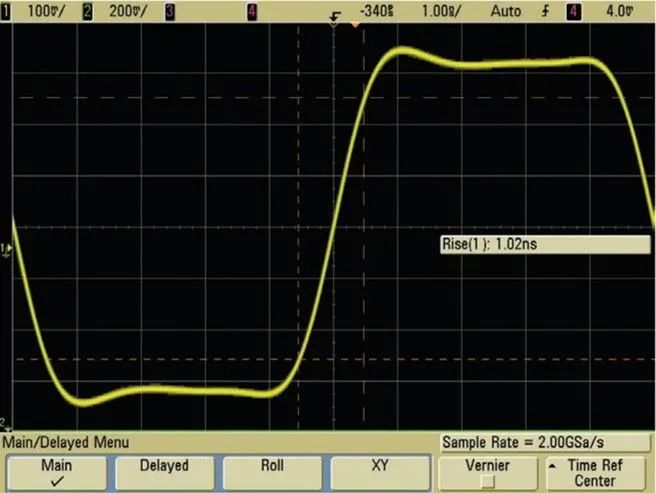
圖 6：采用是德科技 500-MHz 帶寬示波器以 2 GSa/s 的速率進行采樣，可以精確測量這個邊沿速度為 1 ns 的 100-MHz 時鐘信號

那么，如果我們將采樣率增大一倍，使其達到 4 GSa/s，再以相同的 500-MHz 帶寬示波器（fBW x 8）采樣，結果又會怎樣呢？您可能會直觀地認為該示波器將會獲得更佳的波形和測量結果。但正如圖 7 所示，您只能取得很小的改進。如果仔細觀察這兩個波形圖（圖 6 和圖 7），您將會發現，以 4 GSa/s（fBW x 8）采樣時，顯示的波形中僅有輕微的預沖和過沖。但是，上升時間測量顯示相同的結果（1.02 ns）。波形保真度略有提高的關鍵在于：當此示波器的采樣率與帶寬之比由 4:1（2 GSa/s）升至 8:1（4 GSa/s）時，沒有引入其他的誤差源。這就引出了我們的一個主題：如果違背 Nyquist 規則二會怎么樣呢？Nyquist 強調必須等間隔進行采樣。用戶在評測數字存儲示波器時，往往會忽視這一重要規則。

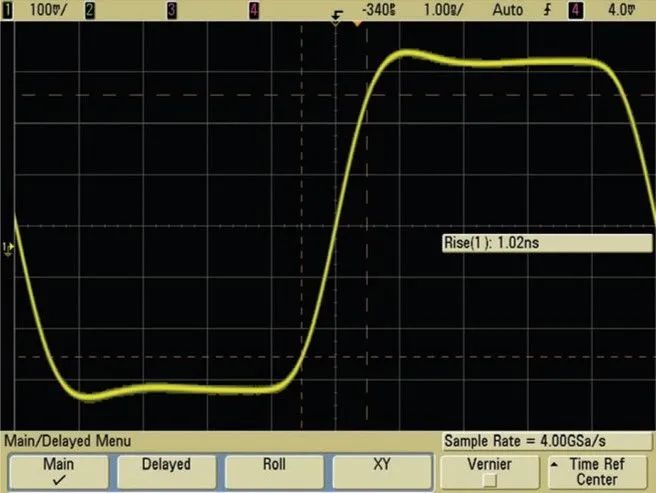
圖 7：采用是德科技 500-MHz 帶寬示波器以 4 GSa/s 采樣，與 2 GSa/s 采樣相比，對測量效果的提高微乎其微。

審核編輯：湯梓紅