微分(D)項是PID控制器的一個組成部分,它對系統的控制輸出做出反應,以減小系統的過度調節和減小響應的快速變化。微分項的作用是在控制系統中引入一個滯后效應,以幫助系統平穩響應。
以下是微分(D)項的詳細介紹:
1. 作用原理:微分項的計算基于誤差的變化率,通常是誤差隨時間的導數。微分項根據誤差的變化率來計算控制輸出。微分項的數學表達式如下:
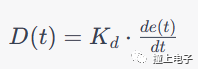
2. 影響:微分項對系統的控制輸出有兩個主要作用:首先,它減小系統的過度調節,防止振蕩;其次,它幫助減小系統響應的快速變化,使系統更穩定。微分項通常在系統的短期變化和噪聲中起關鍵作用,對系統的瞬時響應有較大影響。 3. 微分時間常數:微分時間常數T(d)是一個重要參數,它控制了微分項的響應速度。較大的T(d)值會導致微分項的響應較慢,較小的T(d)值會導致響應較快。通過調整T(d),可以平衡系統的響應速度和穩定性。 4. 調節:調節微分增益K(d)和微分時間常數T(d)是調整PID控制器性能的關鍵。根據具體應用,您可能需要不同的K(d)和T(d)值。一種常見的調節方法是通過試驗和模擬來找到合適的K(d)和T(d)值,以使系統能夠快速響應和保持穩定。
5. 特點:微分項主要用于減小過度調節和平穩系統的響應,因此在系統的瞬時響應中起關鍵作用。如果微分增益K(d)設置得過高,可能會導致系統過度調節或引入噪聲。如果微分增益設置得過低,系統可能無法減小響應的快速變化。
在PID控制器中,微分項通常與比例項和積分項一起使用,以綜合控制系統的性能。合理設置微分增益K(d)和微分時間常數T(d)是PID控制器調節的關鍵,因為它們直接影響了系統的響應速度和穩定性。通過仔細調整微分項,可以實現系統的精確控制和穩定性。微分(D)項通常在實際的PID控制器實現中需要計算誤差的變化率,以計算微分項的控制輸出。
下面是一個簡單的C語言示例代碼,演示如何計算微分項的控制輸出:
#include // PID控制器參數float Kd = 1.0; // 微分增益float Td = 0.1; // 微分時間常數// 全局變量用于存儲上一次的誤差float previousError = 0.0;// 計算微分項float calculateDerivative(float error, float deltaTime) { // 計算誤差的變化率 float errorChange = (error - previousError) / deltaTime;
// 計算微分項的控制輸出 float derivativeOutput = Kd * errorChange * Td;
// 更新上一次的誤差 previousError = error;
return derivativeOutput;}int main() { float setpoint = 100.0; // 期望值 float processVariable = 80.0; // 實際測量值 float error = setpoint - processVariable; float deltaTime = 0.1; // 采樣時間間隔 // 計算微分項的控制輸出 float output = calculateDerivative(error, deltaTime); // 輸出結果 printf("Derivative Output: %f\n", output); return 0;}
在上面的示例中,我們定義了微分增益K(d)和微分時間常數T(d),它們用于調整微分項的影響。calculateDerivative 函數接受誤差值和采樣時間間隔作為參數,然后通過計算誤差的變化率來計算微分項的控制輸出。還使用一個全局變量 previousError來跟蹤上一次的誤差值,以計算誤差的變化率。
-
PID
+關注
關注
35文章
1473瀏覽量
85826 -
代碼
+關注
關注
30文章
4828瀏覽量
69058 -
控制算法
+關注
關注
4文章
166瀏覽量
21797
發布評論請先 登錄
相關推薦




 控制算法PID之微分控制(D)的原理和示例代碼
控制算法PID之微分控制(D)的原理和示例代碼














評論