作者:智林
引言
點(diǎn)云配準(zhǔn)(點(diǎn)云配準(zhǔn)初識(shí))的目的是計(jì)算不同視角下若干組具有共視關(guān)系點(diǎn)云的空間變換關(guān)系(位置和姿態(tài)),從而將這些點(diǎn)云統(tǒng)一到一個(gè)坐標(biāo)系下,進(jìn)而得到被觀測(cè)物體的整體信息。那么,我們?nèi)绾斡?jì)算這種變換關(guān)系呢?或者說(shuō)其對(duì)應(yīng)的數(shù)學(xué)問(wèn)題是怎么樣的呢?
其實(shí),點(diǎn)云配準(zhǔn)本質(zhì)就是一個(gè)優(yōu)化問(wèn)題,從幾何關(guān)系來(lái)說(shuō)就是使具有共視關(guān)系點(diǎn)云的空間距離足夠小,接近于零;從空間分布關(guān)系來(lái)說(shuō),就是最大化共視關(guān)系的點(diǎn)落在所在柵格的概率分布。因此,對(duì)于一個(gè)點(diǎn)云配準(zhǔn)這個(gè)技術(shù)問(wèn)題,我們需要定義優(yōu)化函數(shù),運(yùn)用優(yōu)化方法去求解所定義的優(yōu)化問(wèn)題。所需要用到的數(shù)學(xué)知識(shí)包括,空間變換的表示,矩陣分析,優(yōu)化方法(常見的高斯-牛頓法,LM算法),導(dǎo)數(shù)求解等等。
接下來(lái)的內(nèi)容就是分享其中的一部分?jǐn)?shù)學(xué)基礎(chǔ)知識(shí),其中優(yōu)化方法和導(dǎo)數(shù)求解建議大家先去看看高博的《視覺(jué)slam十四講》,這里可能就不展開了,因?yàn)橐坏┱归_就太雜了,遲遲無(wú)法進(jìn)入點(diǎn)云配準(zhǔn)算法的講解(要講的東西實(shí)在太多太多),所以大家自己先去學(xué)習(xí)一下吧!后面如果有機(jī)會(huì),我在對(duì)這部分內(nèi)容詳細(xì)講解。其實(shí),這兩部分是自動(dòng)駕駛算法中的關(guān)鍵基礎(chǔ)知識(shí),大家必須都要會(huì),不然無(wú)論是看論文還是看代碼都是一臉茫然,快去自己看書學(xué)習(xí),不懂的可以加入交流群一起討論交流。下面,我們就著重講解空間變換關(guān)系的表示及其參數(shù)化以及剛性配準(zhǔn)的基本數(shù)學(xué)問(wèn)題表達(dá)與求解,和對(duì)應(yīng)的c++代碼。
空間變換及其參數(shù)化
我們已經(jīng)知道點(diǎn)云配準(zhǔn)就是計(jì)算空間變換關(guān)系,也就是位置和姿態(tài)。那么,用什么方法表示位置和姿態(tài)呢?每個(gè)表示方法又有什么優(yōu)點(diǎn)和缺點(diǎn)呢?實(shí)際運(yùn)用中我們?nèi)绾芜x擇呢?帶著這些有趣的問(wèn)題,開始接下來(lái)的學(xué)習(xí)。
向量在三維空間中的表示方法
我們以后再?zèng)]有特別說(shuō)明的情況下,討論的都是三維空間,所討論的點(diǎn)云配準(zhǔn)也是三維點(diǎn)云配準(zhǔn)。那么,我們首先要知道如何表示三維空間中的點(diǎn),以及兩點(diǎn)連線構(gòu)成的向量。可能,這里大家會(huì)有疑問(wèn),我知道怎么表示點(diǎn)不就行了嗎,為什么還要表示向量呢?原因是,點(diǎn)云配準(zhǔn)需要求解的空間變換關(guān)系除了位置之外,還有姿態(tài)。點(diǎn)的信息只能刻畫位置,兩點(diǎn)連接所形成的向量就可以表示姿態(tài),并且向量本身也可以表示位置,所以我們的核心實(shí)則是研究向量,其既包括位置信息又包括姿態(tài)信息。
在三維空間中,無(wú)論是研究點(diǎn)還是由點(diǎn)構(gòu)成的向量,我們都必須要指定坐標(biāo)系,只有在某個(gè)指定的坐標(biāo)系下才能去研究點(diǎn)的表示以及向量的表示。
線性代數(shù)的知識(shí)告訴我們,只需要找到三維空間的一組基,就可以利用這組基表示三維空間下的任意向量。簡(jiǎn)單回顧一下基的定義:
在線性代數(shù)中,一個(gè)向量空間 的基(basis)是指滿足以下兩個(gè)性質(zhì)的向量集合:
生成性質(zhì) (Spanning Property):基中的向量能夠通過(guò)線性組合生成向量空間 中的任意向量。換句話說(shuō),對(duì)于任意 中的向量 ,存在基中的向量 和標(biāo)量 使得
線性無(wú)關(guān)性質(zhì)(Linear Independence Property):基中的向量之間不存在非零的線性組合使得結(jié)果為零向量。換句話說(shuō),如果 ,其中 是標(biāo)量,且不全為零,則基中的向量線性相關(guān)。
假設(shè)我們已經(jīng)找到了三維空間的一組基 , 那么, 任意一個(gè)向量 在這組基下可以表示為:
這里 稱為 在此基下的坐標(biāo) 。由此可見,坐標(biāo)的具體取值,一是和向量本身有關(guān),,二是和坐標(biāo)系 (基) 的選取有關(guān)。通常情況下,坐標(biāo)系由 3 個(gè)正交的坐標(biāo)軸組成,也就是我們常說(shuō)的笛卡爾坐標(biāo)系的x,y,z軸,所選擇的基就是
在這里,為了方便后續(xù)對(duì)向量的討論,這里引出一個(gè)向量外積的概念,這個(gè)概念很簡(jiǎn)單,但是在slam領(lǐng)域非常重要和實(shí)用。先簡(jiǎn)單回顧一下高中學(xué)到的向量?jī)?nèi)積是啥。對(duì)于任意的,內(nèi)積的定義為:
其中, 指向量 的夾角。雖然內(nèi)積的概念從高中就已經(jīng)知道了,但是那時(shí)候畢竟是為了應(yīng)付高考,現(xiàn)在我們可以想一想這個(gè)有啥實(shí)際的工程或者學(xué)術(shù)價(jià)值。這里,我就拋磚引玉一下,內(nèi)積在實(shí)際工程中,可以計(jì)算其數(shù)值與零比較大小,判斷兩個(gè)向量的夾角是否超過(guò)90度,進(jìn)而判斷移動(dòng)的智能體是否發(fā)生空間位置的變化(大家好好琢磨,其中的一個(gè)向量是點(diǎn)的法向量,另外一個(gè)向量是當(dāng)前位置與點(diǎn)連線構(gòu)成的向量)。話不多時(shí),趕緊來(lái)聊聊新的知識(shí),向量的外積,向量外積的定義為:
外積的一個(gè)重要性質(zhì)是:外積的結(jié)果是一個(gè)向量,并且垂直于這兩個(gè)向量,其大小為。這里,有一個(gè)重要的符號(hào)引入,即,其作用就是將一個(gè)向量映射為一個(gè)矩陣,并且這個(gè)矩陣是一一映射(單射),這個(gè)矩陣是反對(duì)稱的,稱為反對(duì)稱矩陣。其定義為:對(duì)于任意向量,有:
同理,對(duì)于任意一個(gè)反對(duì)稱矩陣,我們有:。
坐標(biāo)系間的歐式變換與旋轉(zhuǎn)矩陣
根據(jù)上面的分析,我們知道我們研究的最底層?xùn)|西是向量,這個(gè)向量只有在定義了坐標(biāo)系之后才有意義。那現(xiàn)在我們?cè)诨剡^(guò)頭想一想點(diǎn)云配準(zhǔn)的核心是什么?點(diǎn)云配準(zhǔn)是計(jì)算兩個(gè)具有共視關(guān)系點(diǎn)云的變換關(guān)系,這里的具有共視關(guān)系區(qū)域的每個(gè)點(diǎn)大家可以理解成向量,這些點(diǎn)(向量)是在不同時(shí)刻不同坐標(biāo)系下定義的,因此我們所要求得坐標(biāo)變換關(guān)系也就是坐標(biāo)系的變換關(guān)系。
通過(guò)上面的分析,我想大家應(yīng)該可以比較徹底的弄明白為啥書上講到點(diǎn)云配準(zhǔn),或者slam,一定要首先講解坐標(biāo)系的歐式變換,只有理解了,才會(huì)覺(jué)得書上的內(nèi)容不是那么突兀和跳躍,而是非常合理的安排,哈哈。那下面我們就開始介紹坐標(biāo)系的歐式變換,進(jìn)而直接引出旋轉(zhuǎn)矩陣。
兩個(gè)坐標(biāo)系之間的運(yùn)動(dòng)由一個(gè)旋轉(zhuǎn)加上一個(gè)平移組成,這種運(yùn)動(dòng)稱為剛體運(yùn)動(dòng)。由于剛體運(yùn)動(dòng)保持了向量的長(zhǎng)度和夾角,相當(dāng)于把一個(gè)剛體原封不動(dòng)地進(jìn)行移動(dòng)或旋轉(zhuǎn),不改變它自身的形狀,因此它是一種歐式變換(Euclidean Transform)。這里大家可能有這樣的疑問(wèn),夾角為啥沒(méi)有變化,我坐標(biāo)系都發(fā)生旋轉(zhuǎn)了,向量的夾角怎么還沒(méi)有變化呢?沒(méi)有這樣的疑問(wèn)最好,有這樣的疑問(wèn)也沒(méi)事,因?yàn)橹皇墙^大多數(shù)書上沒(méi)有怎么解釋這個(gè)夾角是什么意思。這里的夾角通常指的是兩個(gè)向量之間的角度。在不同坐標(biāo)系中,兩個(gè)向量之間的夾角是不變的。這意味著,如果你有兩個(gè)向量 和,它們的夾角在剛體運(yùn)動(dòng)時(shí)會(huì)保持不變。無(wú)論剛體怎么運(yùn)動(dòng),這兩個(gè)向量之間的夾角都不會(huì)發(fā)生變化。
這里借用高博書上的一個(gè)例子,剛好我自己最近也弄到了一臺(tái)mate60pro昆侖玻璃加持,摔不壞,但是我沒(méi)有嘗試過(guò),哈哈哈。想象你把手機(jī)拋到空中、在它落地掉碎之前,只可能有空間位置和姿態(tài)的不同,而它自己的長(zhǎng)度、各個(gè)面的角度等性質(zhì)不會(huì)有任何變化。手機(jī)并不會(huì)像橡皮那樣一會(huì)兒被擠扁,一會(huì)兒被拉長(zhǎng)。此時(shí),我們說(shuō)手機(jī)坐標(biāo)系到世界坐標(biāo)之間,相差了一個(gè)歐氏變換。
有了這些基礎(chǔ)之上,我們終于可以引出旋轉(zhuǎn)矩陣了。假設(shè)某個(gè)單位正交基經(jīng)過(guò)了一次旋轉(zhuǎn)變成(,那么對(duì)于向量 而言,它在兩個(gè)坐標(biāo)系下 (同一個(gè)點(diǎn)參考系不同) 的坐標(biāo)分別為和。由于 本身沒(méi)有改變,因此:
對(duì)上面的式子做一個(gè)小小的變形,兩邊同時(shí)左乘,左邊直接變成了單位矩陣,因此有:
我們將中間的矩陣記為,其描述了同一個(gè)向量在旋轉(zhuǎn)前后(姿態(tài)發(fā)生變化前后)的坐標(biāo)坐標(biāo)變化關(guān)系,這里并沒(méi)有表達(dá)出位置的關(guān)系,因此稱為旋轉(zhuǎn)矩陣(Rotation Matrix)。
旋轉(zhuǎn)矩陣有一個(gè)非常重要的性質(zhì):。
這里的證明大家可以看書,比較簡(jiǎn)單,但是這個(gè)性質(zhì)非常非常重要,后面我們慢慢回味。旋轉(zhuǎn)矩陣的概念可以推廣到多維,將維旋轉(zhuǎn)矩陣的集合定義為:
式中 SO(n)表示特殊正交群,旋轉(zhuǎn)矩陣即描述了兩個(gè)坐標(biāo)的姿態(tài)變換關(guān)系:
如果考慮平移,則可以更新表示為。因此兩個(gè)坐標(biāo)系的剛體運(yùn)動(dòng)可以由和進(jìn)行描述,但是該變換不是一個(gè)線性變換。假設(shè)我們進(jìn)行了兩次坐標(biāo)變換:,這里簡(jiǎn)單說(shuō)明一下, 是指“把坐標(biāo)系 2 的向量變換到坐標(biāo)系 1” 中,從右往左讀,這里借鑒了高博的十四講的做法,當(dāng)然你也可以按照自己的習(xí)慣反過(guò)來(lái)都一樣。
那么,從 到 的變換為
這樣的形式在變換多次之后會(huì)顯得很不簡(jiǎn)約。因此,引人齊次坐標(biāo)和變換矩陣,重寫上式:
將原始的三維向最末尾增加1個(gè)維度,取值為1,該四維向量被稱為齊次坐標(biāo),而矩陣寫作,稱為變換矩陣(Transform Matrix),這種類型的矩陣又被稱為特殊歐式群:
式中,為 3×3 的矩陣, 的逆表示進(jìn)行反向的變換:
有了變換矩陣這個(gè)工具之后,我們就可以對(duì)上面連續(xù)進(jìn)行兩次變換的疊加有一個(gè)簡(jiǎn)單直觀的表示,用 表示 的齊次坐標(biāo)。那么依靠齊次坐標(biāo)和變換矩陣,兩次變換的疊加就可以有很好的形式:
旋轉(zhuǎn)向量/角軸/軸角
旋轉(zhuǎn)矩陣描述了物體運(yùn)動(dòng)的3自由度旋轉(zhuǎn),在此基礎(chǔ)上引入了變換矩陣,描述了6自由度的三維剛體運(yùn)動(dòng),看似已經(jīng)足夠了,我們已經(jīng)找到了點(diǎn)云配準(zhǔn)所需計(jì)算的變換運(yùn)動(dòng)的表達(dá)形式。是的,的確是可以了,在計(jì)算的時(shí)候一般也是輸出和,然后將點(diǎn)云投影到統(tǒng)一的坐標(biāo)系下,最終得到點(diǎn)云。
但是,通過(guò)矩陣表示方式存在兩個(gè)明顯的不足,分別是:
旋轉(zhuǎn)矩陣有9個(gè)量,但是一次選準(zhǔn)只有3個(gè)自由度;變換矩陣有16個(gè)量,但是一次歐式變換只有6個(gè)自由度。因此,這種表示方式存在冗余,占用的內(nèi)存多。由此,是不是可以找到一種緊湊的表達(dá)形式呢?
上述分析中提到旋轉(zhuǎn)矩陣有一個(gè)重要的性質(zhì):旋轉(zhuǎn)矩陣是行列式為1的正交矩陣。因此在后續(xù)估計(jì)或者優(yōu)化一個(gè)旋轉(zhuǎn)矩陣時(shí),我們必要要保持這一性質(zhì),這樣會(huì)讓求解變得麻煩困難。
首先,可以肯定的說(shuō),存在一種緊湊的方式來(lái)描述平移和旋轉(zhuǎn),用一個(gè)三維向量表達(dá)旋轉(zhuǎn),用一個(gè)六維的向量表達(dá)變換。事實(shí)上,任意旋轉(zhuǎn)都可以用一個(gè)旋轉(zhuǎn)軸和一個(gè)旋轉(zhuǎn)角來(lái)刻畫。于是,我們可以使用一個(gè)向量,其方向與旋轉(zhuǎn)軸一致,而長(zhǎng)度等于旋轉(zhuǎn)角。這種問(wèn)量稱為**旋轉(zhuǎn)向量(或軸角/角軸,Axis-Angle)**,只需一個(gè)三維向量即可描述旋轉(zhuǎn)。同樣,對(duì)于變換矩陣,我們使用一個(gè)旋轉(zhuǎn)向量和一個(gè)平移向量即可表達(dá)一次變換。這時(shí)的變量維數(shù)正好是六維。具體表達(dá)形式為:
式中, 與旋轉(zhuǎn)軸方向一致的單位向量, 為角度。
乍一看,這種表示方式好極了,表示6自由度的變換恰到好處非常緊湊。但是,旋轉(zhuǎn)向量也存在缺點(diǎn):
使用軸角表示方式無(wú)法表達(dá)兩次連續(xù)的旋轉(zhuǎn),由于兩次旋轉(zhuǎn)的旋轉(zhuǎn)軸會(huì)不一樣,因此旋轉(zhuǎn)角度不能直接相加。
當(dāng)旋轉(zhuǎn)角度為 0°或者 180°時(shí),羅德里格斯公式失效,此時(shí)的旋轉(zhuǎn)矩陣為 0。可以理解為這種情況下旋轉(zhuǎn)角具有無(wú)數(shù)多種情況。由于旋轉(zhuǎn)矩陣到軸角表示法的映射關(guān)系是一對(duì)多的關(guān)系,因此存在多種軸角組合對(duì)應(yīng)一種旋轉(zhuǎn)矩陣的情況。
這里簡(jiǎn)單解釋一下,因?yàn)楹竺嫖覀儐为?dú)會(huì)講各種變換關(guān)系之間的轉(zhuǎn)化,其中羅德里格斯公式也會(huì)詳細(xì)介紹,這里直接給出:
羅德里格斯公式描述的是旋轉(zhuǎn)向量到旋轉(zhuǎn)矩陣的轉(zhuǎn)換關(guān)系,當(dāng)或者時(shí),。
歐拉角
通過(guò)上述分析知道,旋轉(zhuǎn)矩陣和旋轉(zhuǎn)向量都可以表示旋轉(zhuǎn),但各自又都有缺點(diǎn),不是很完美。除了已經(jīng)談到自身固有的缺點(diǎn)之后,它們兩還有一個(gè)非常大的bug,那就是不直觀。給你一個(gè)旋轉(zhuǎn)矩陣或者旋轉(zhuǎn)向量在你面前,比較難去想像這個(gè)旋轉(zhuǎn)究竟是什么樣的,或者比較簡(jiǎn)單的旋轉(zhuǎn)向量還可以,但是一旦旋轉(zhuǎn)軸復(fù)雜一些,就懵了。那下面就介紹一個(gè)非常直觀的表示旋轉(zhuǎn)的一種方式------歐拉角。
歐拉角使用了3個(gè)分離的轉(zhuǎn)角,把一個(gè)旋轉(zhuǎn)分解成 3 次繞不同軸的旋轉(zhuǎn)。對(duì)于我們來(lái)說(shuō),很容易理解繞單個(gè)軸旋轉(zhuǎn)的過(guò)程。但是,這里也帶來(lái)一定的問(wèn)題,由于分解方式有許多種,所以歐拉角也存在著眾多不同的、易于混淆的定義方法。例如,先繞 軸,再繞 軸,最后繞 軸旋轉(zhuǎn),就得到了一個(gè) 軸的旋轉(zhuǎn),同理也可以得到,,甚至可以定義,等等。
這種定義方式上的不確定性帶來(lái)了很多實(shí)際當(dāng)中的困難,但是在某一個(gè)特定的領(lǐng)域,歐拉角通常有統(tǒng)一的定義方式。在航天航空領(lǐng)域,歐拉角便有一種約定俗成的定義方式,便是用“偏航- 俯仰-滾轉(zhuǎn)"(yaw-pitch-roll)3個(gè)角度來(lái)描述一個(gè)旋轉(zhuǎn)。它等價(jià)于 軸的旋轉(zhuǎn),因此就以 為例。假設(shè)一個(gè)剛體的前方( 朝向我們的方向)為 軸,右側(cè)為軸,上方為軸,如下圖所示。那么, 轉(zhuǎn)角相當(dāng)于把任意旋轉(zhuǎn)分解成以下 3 個(gè)軸上的轉(zhuǎn)角:
繞物體的 軸旋轉(zhuǎn),得到偏航角 yaw。
繞旋轉(zhuǎn)之后的軸旋轉(zhuǎn),得到俯仰角 pitcho
繞旋轉(zhuǎn)之后的 軸旋轉(zhuǎn),得到滾轉(zhuǎn)角 roll。
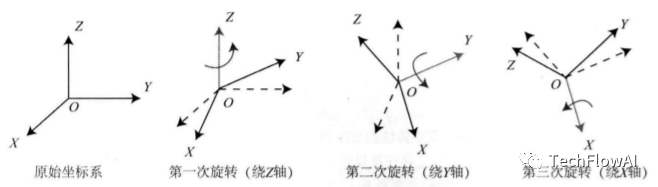
此時(shí),可以使用 這樣一個(gè)三維的向量描述任意旋轉(zhuǎn),并且這個(gè)非常直觀。所以在跨行業(yè)或者跨模塊協(xié)作的時(shí)候,一定要問(wèn)清楚對(duì)方是哪一種歐拉角。
歐拉角一般可以定義為靜態(tài)和動(dòng)態(tài)兩種形式。在介紹靜態(tài)和動(dòng)態(tài)兩種形式之前,首先定義繞各個(gè)旋轉(zhuǎn)軸轉(zhuǎn)相應(yīng)角度時(shí)所應(yīng)對(duì)的選準(zhǔn)矩陣。
當(dāng)繞軸旋轉(zhuǎn) 角度時(shí)對(duì)應(yīng)的旋轉(zhuǎn)矩陣為:
當(dāng)繞軸旋轉(zhuǎn) 角度時(shí)對(duì)應(yīng)的旋轉(zhuǎn)矩陣為:
當(dāng)繞軸旋轉(zhuǎn) 角度時(shí)對(duì)應(yīng)的旋轉(zhuǎn)矩陣為:
這三個(gè)矩陣怎么得到的,大家可以去看我b站視頻,因?yàn)檫@里畫圖太麻煩了,實(shí)則非常簡(jiǎn)單,大家直接百度也可以搜到。那下面就來(lái)介紹靜態(tài)和動(dòng)態(tài)歐拉角。
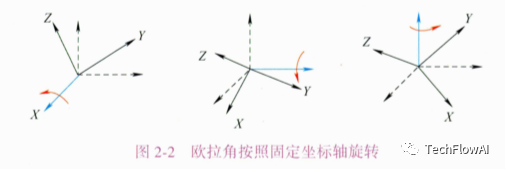
所謂靜態(tài)的歐拉角指繞世界坐標(biāo)系三個(gè)固定軸的旋轉(zhuǎn),旋轉(zhuǎn)過(guò)程中世界坐標(biāo)系的三個(gè)軸不發(fā)生變化,也稱為外旋旋轉(zhuǎn)方式。如圖 2-2 所示,按照外旋方式,X-Y- 旋轉(zhuǎn)順序 (指先繞固定軸X 旋轉(zhuǎn) α, 再繞固定軸 Y 旋轉(zhuǎn) , 最后繞固定軸 旋轉(zhuǎn) ), 這種形式的歐拉角也稱為 RPY 角,α、β和γ對(duì)應(yīng)航空領(lǐng)域的 Roll、Pitch 和 Yaw。最終可得旋轉(zhuǎn)矩陣
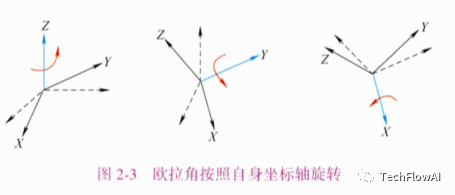
而動(dòng)態(tài)歐拉角是指繞物體坐標(biāo)系三個(gè)軸的旋轉(zhuǎn),由于物體旋轉(zhuǎn)過(guò)程中坐標(biāo)軸隨著旋轉(zhuǎn)變換運(yùn)動(dòng),也稱為內(nèi)旋旋轉(zhuǎn)方式。如圖 2-3 所示,此時(shí)若按照 的順序依次旋轉(zhuǎn) 、 和 α 的角度,這種形式的歐拉角也稱為 歐拉角,則最終可得旋轉(zhuǎn)矩陣
這里要注意:內(nèi)旋時(shí)繞自身坐標(biāo)系旋轉(zhuǎn),右乘坐標(biāo)向量,坐標(biāo)系(基底)在變換, 變換;外旋時(shí)繞固定坐標(biāo)系旋轉(zhuǎn),左乘坐標(biāo)向量,坐標(biāo)(向量) 在變換,行變換。這種情況下如果使用 RPY 角進(jìn)行描述,即繞物體的 軸旋轉(zhuǎn) , 得到偏航角 Yaw, 繞旋轉(zhuǎn)之后的 Y軸旋轉(zhuǎn),得到俯仰角 Pitch, 繞旋轉(zhuǎn)之后的 軸旋轉(zhuǎn) , 得到滾轉(zhuǎn)角 Roll。因此 Yaw、Pitch 和Roll 分別對(duì)應(yīng) 、 和
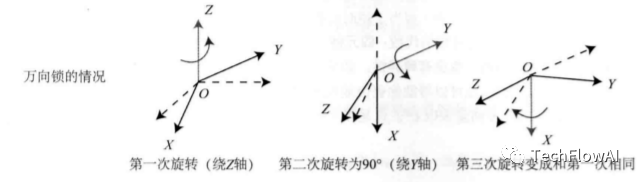
通過(guò)上述分析,可以看出來(lái)歐拉角非常直觀,便于立即。但是這個(gè)方法同樣也存在缺點(diǎn),即著名的萬(wàn)向鎖(或萬(wàn)向節(jié)死鎖)(Gimbal Lock)問(wèn)題:在俯仰角為 時(shí), 第一次旋轉(zhuǎn)與第三次旋轉(zhuǎn)將使用同一個(gè)軸,使得系統(tǒng)丟失了一個(gè)自由度(由3次旋轉(zhuǎn)變成了2次旋轉(zhuǎn))。這被稱為奇異性問(wèn)題,在其他形式的歐拉角中也同樣存在。理論上可以證明,只要想用3 個(gè)實(shí)數(shù)來(lái)表達(dá)三維旋轉(zhuǎn),都會(huì)不可避免地碰到奇異性問(wèn)題。由于這種原理,歐拉角不適用于插值和迭代,往往只用于人機(jī)交互中。我們也很少在 SLAM 程序中直接使用歐拉角表達(dá)姿態(tài),同樣不會(huì)在濾波或優(yōu)化中使用歐拉角表達(dá)旋轉(zhuǎn)(因?yàn)樗哂衅娈愋?。不過(guò),若你想驗(yàn)證自己的算法是否有錯(cuò),轉(zhuǎn)換成歐拉角能夠幫你快速分辨結(jié)果是否正確。
四元數(shù)
四元數(shù)最早于 1843 年由哈密頓(William Rowan Hamilton ) 發(fā)明,作為復(fù)數(shù) ( Complex Numbers) 的擴(kuò)展。直到1985 年才由 Shoemake 把四元數(shù)引入到計(jì)算機(jī)圖形學(xué)中。四元數(shù)在一 些方面優(yōu)于歐拉角、軸角和旋轉(zhuǎn)矩陣,比如解決萬(wàn)向鎖問(wèn)題。由于僅需存儲(chǔ)4 個(gè)浮點(diǎn)數(shù),相比矩陣更加輕量,使得四元數(shù)解決求逆、串聯(lián)(多個(gè)變換的疊加變換)等操作,相比矩陣更加高效。總結(jié)一下,四元數(shù)具有一下兩個(gè)良好的性質(zhì):一是其表示旋轉(zhuǎn)是緊湊的;二是其不存在奇異性。
這里應(yīng)用高博十四講中的做法引出單位四元數(shù)可以表示三維旋轉(zhuǎn)。例如,當(dāng)我們想要將復(fù)平面的向量旋轉(zhuǎn) 角時(shí),可以給這個(gè)復(fù)向量乘以 e。這是極坐標(biāo)表示的復(fù)數(shù),它也可以寫成普通的形式,只要使用歐拉公式即可:
這正是一個(gè)單位長(zhǎng)度的復(fù)數(shù)。所以,在二維情況下,旋轉(zhuǎn)可以由單位復(fù)數(shù)來(lái)描述。類似地,我們會(huì)看到,三維旋轉(zhuǎn)可以由單位四元數(shù)來(lái)描述。
一個(gè)四元數(shù)由一個(gè)實(shí)部和三個(gè)虛部構(gòu)成,表達(dá)形式如下:
其中,,,為四元數(shù)的三個(gè)虛部。這三個(gè)虛部滿足以下關(guān)系式:
為了方便表示四元數(shù),通常用一個(gè)標(biāo)量和一個(gè)向量來(lái)表達(dá)四元數(shù):
這里, 稱為四元數(shù)的實(shí)部,而 稱為它的虛部。如果一個(gè)四元數(shù)的虛部為 0, 則稱為實(shí)四元數(shù);反之,若它的實(shí)部為0, 則稱為虛四元數(shù)。
四元數(shù)也可以進(jìn)行各種運(yùn)算,例如:加法。乘法、共軛,求逆,數(shù)乘等等,這些也都是我們工程或者學(xué)習(xí)中經(jīng)常使用。這里直接給出其結(jié)論:

對(duì)四元數(shù)有了初步的了解之后,下面我們來(lái)考慮四元數(shù)如何表示旋轉(zhuǎn)?
可以用四元數(shù)表達(dá)對(duì)一個(gè)點(diǎn)的旋轉(zhuǎn)。假設(shè)有一個(gè)空間三維點(diǎn) 。以及一個(gè)由單位四元數(shù) 指定的旋轉(zhuǎn)。三維點(diǎn) 經(jīng)過(guò)旋轉(zhuǎn)之后變?yōu)?。如果使用矩陣描述,那么有。而如果用四元數(shù)描述旋轉(zhuǎn),它們的關(guān)系又如何表達(dá)呢?
首先,把三維空間點(diǎn)用一個(gè)虛四元數(shù)來(lái)描述:
相當(dāng)于把四元數(shù)的 3 個(gè)虛部與空間中的 3 個(gè)軸相對(duì)應(yīng)。那么,旋轉(zhuǎn)后的點(diǎn) 可表示為這樣的乘積:
這里的乘法均為四元數(shù)乘法,結(jié)果也是四元數(shù)。最后把的虛部取出,即得旋轉(zhuǎn)之后點(diǎn)的坐標(biāo)。這是為什么呢?因?yàn)樯鲜龉降挠?jì)算結(jié)果的實(shí)部為 0, 故為純虛四元數(shù)。
關(guān)于四元數(shù)更多的知識(shí),以及上述我所提到的知識(shí)的深入講解,大家可以參考論文《Quaternion kinematics for the error-state Kalman filter》。
總結(jié)
這一小節(jié)我們主要介紹了如何表示三自由度的旋轉(zhuǎn),講解了四種表示方式,分別為:旋轉(zhuǎn)矩陣,旋轉(zhuǎn)向量,歐拉角和四元數(shù),它們各有其優(yōu)勢(shì)和不足,大家可以自己思考一下,回顧一下自己是否掌握了。現(xiàn)在我們已經(jīng)解決了一個(gè)非常棘手的問(wèn)題,就是用什么工具來(lái)表示點(diǎn)云配準(zhǔn)中的變換關(guān)系。但是,我們有面臨一個(gè)苦惱,這么多方法我怎么選擇呀?或者說(shuō)我計(jì)算出其中一個(gè)能不能得到另外三個(gè)?答案是肯定的,它們之間可以相互轉(zhuǎn)換,那一節(jié)我們將探究空間變換的不同表示方法之間的互相轉(zhuǎn)換。
[1] 高翔等,視覺(jué)slam十四講[M].
[2] 郭浩,點(diǎn)云配準(zhǔn)從入門到精通[M].
[3] Sola J. Quaternion kinematics for the error-state Kalman filter[J]. arXiv preprint arXiv:1711.02508, 2017.
編輯:黃飛
-
算法
+關(guān)注
關(guān)注
23文章
4630瀏覽量
93358 -
C++
+關(guān)注
關(guān)注
22文章
2114瀏覽量
73858 -
自動(dòng)駕駛
+關(guān)注
關(guān)注
785文章
13932瀏覽量
167010 -
點(diǎn)云配準(zhǔn)
+關(guān)注
關(guān)注
0文章
4瀏覽量
808
原文標(biāo)題:深度剖析點(diǎn)云配準(zhǔn)中的數(shù)學(xué)基礎(chǔ)
文章出處:【微信號(hào):3D視覺(jué)工坊,微信公眾號(hào):3D視覺(jué)工坊】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
基于深度學(xué)習(xí)的三維點(diǎn)云配準(zhǔn)方法
一種快速的三維點(diǎn)云自動(dòng)配準(zhǔn)方法
基于特征點(diǎn)精度提純的圖像配準(zhǔn)改進(jìn)算法
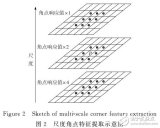
具有SIFT描述的多尺度角點(diǎn)圖像配準(zhǔn)
基于平移域估計(jì)的點(diǎn)云全局配準(zhǔn)算法

使用PCL進(jìn)行點(diǎn)云數(shù)據(jù)粗配準(zhǔn)算法的研究資料分析
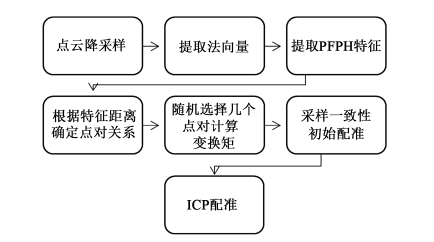
一種多幅點(diǎn)云數(shù)據(jù)與紋理序列自動(dòng)配準(zhǔn)方法

基于機(jī)械臂的車輛輪廓掃描定位及數(shù)據(jù)配準(zhǔn)
自動(dòng)駕駛?cè)谠挘撼S玫?b class='flag-5'>點(diǎn)云配準(zhǔn)方法以及未來(lái)發(fā)展方向
三維點(diǎn)云配準(zhǔn)的相關(guān)知識(shí)學(xué)習(xí)技巧
SDMNet:大規(guī)模激光雷達(dá)點(diǎn)云配準(zhǔn)的稀疏到稠密匹配網(wǎng)絡(luò)
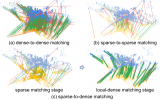
基于深度學(xué)習(xí)的三維點(diǎn)云配準(zhǔn)新方法

三維點(diǎn)云配準(zhǔn)算法,包括4PCS、K-4PCS、SAC-IA、ICP、PCA、深度學(xué)習(xí)方法等





 深度剖析點(diǎn)云配準(zhǔn)中的數(shù)學(xué)基礎(chǔ)
深度剖析點(diǎn)云配準(zhǔn)中的數(shù)學(xué)基礎(chǔ)










評(píng)論