01
限幅消抖濾波
原理
限幅消抖濾波法是一種簡單有效的數字濾波算法,常用于對采集到的離散信號進行去抖動處理。它可以去除信號中的瞬時噪聲和突發干擾,同時保留信號的主要特征。
限幅消抖濾波法的原理是通過設置一個合適的閾值,將信號限制在一個固定的范圍內,并消除信號中的抖動。當信號的變化速度超過閾值時,限制信號的變化幅度,以消除抖動;當信號變化速度較緩時,允許信號在一定范圍內波動,以保留信號的主要特征。在實際應用中,通常將限幅消抖濾波法與其他濾波算法結合使用,以進一步提高濾波效果。
限幅消抖濾波法的優點是簡單易實現,能夠快速去除瞬時噪聲和突發干擾,適用于一些對實時性要求較高的應用場景。但是它也存在一些缺點,如可能會丟失一些信號細節,對信號的頻率特性影響較大等。
在單片機系統中,限幅消抖濾波法可以通過編程實現。具體步驟是:先讀取一組原始信號數據,然后設置一個合適的閾值,將信號限制在一個固定的范圍內,再通過一定的方法消除信號的抖動,最后輸出處理后的濾波信號數據。
代碼
C++
#define MAX_VALUE 100
#define MIN_VALUE -100
#define THRESHOLD 10
int LimitFilter(int input)
{
static int previous_output = 0; // 上一次的輸出值
int output = input; // 當前的輸出值
// 限制輸出值在一定范圍內
if (output > MAX_VALUE) {
output = MAX_VALUE;
} else if (output < MIN_VALUE) {
output = MIN_VALUE;
}
// 消除信號抖動
if (output - previous_output > THRESHOLD) {
output = previous_output + THRESHOLD;
} else if (previous_output - output > THRESHOLD) {
output = previous_output - THRESHOLD;
}
previous_output = output; // 保存當前輸出值
return output;
}
使用示例
這個函數實現了限幅消抖濾波法的基本功能,包括限制輸出值在一定范圍內,以及消除信號抖動。它使用了一個靜態變量來保存上一次的輸出值,以便下一次的濾波操作中使用。
使用這個函數非常簡單,只需要在程序中調用它即可。例如,可以在主函數中讀取一個模擬信號值,并將其傳遞給這個函數進行濾波,然后輸出濾波后的值。示例代碼如下:
C++
#include
int main()
{
int input = 80;
int output = LimitFilter(input);
printf("Input value: %dn", input);
printf("Output value: %dn", output);
return 0;
}
在這個示例中,我們將輸入信號值設為80,并將其傳遞給LimitFilter函數進行濾波。然后將濾波后的值輸出到屏幕上。在實際應用中,可以根據具體的需求來讀取不同的輸入信號值,并將濾波后的結果用于后續的處理。
02
算術平均濾波
原理
算術平均濾波是一種最簡單常用的數字濾波算法之一,也是一種基于時間域的濾波方法。其原理是將連續采集到的一組數據進行加和,并求出其平均值,以此作為濾波后的輸出值。這種方法能夠有效平滑信號,去除噪聲干擾,同時保留信號的趨勢和主要特征。
算術平均濾波的實現方法比較簡單,可以通過下面的步驟來實現:
a. 設置一個固定長度的數據窗口,用于存儲連續采集到的數據。
b. 當有新的數據到達時,將其加入到數據窗口中,并去除窗口中最早的一組數據。
c. 對窗口中的所有數據進行加和,并計算出其平均值作為輸出值。
d. 將輸出值返回給調用者。
算術平均濾波法的優點是簡單易實現,能夠快速平滑信號,去除噪聲干擾,適用于一些信號波動比較緩慢的應用場景。但是它也存在一些缺點,如對信號的時滯影響較大,無法應對快速變化的信號等。
在單片機系統中,算術平均濾波法可以通過編程實現。具體步驟是:先設置一個固定長度的數據窗口,然后讀取一組原始信號數據,并將其加入到數據窗口中,去除窗口中最早的一組數據,再對窗口中的所有數據進行加和,計算出平均值,最后輸出處理后的濾波信號數據。
代碼
下面是一個使用C語言編寫的算術平均濾波法函數的示例代碼:
C++
#define WINDOW_SIZE 5
int MeanFilter(int input)
{
static int data[WINDOW_SIZE] = {0}; // 數據窗口
static int index = 0; // 窗口中最后一個數據的索引
int sum = 0; // 窗口中所有數據的和
int output = 0; // 輸出值
// 將新數據加入到數據窗口中
data[index] = input;
// 更新窗口中最后一個數據的索引
index = (index + 1) % WINDOW_SIZE;
// 計算窗口中所有數據的和
for (int i = 0; i < WINDOW_SIZE; i++) {
sum += data[i];
}
// 計算平均值作為輸出值
output = sum / WINDOW_SIZE;
return output;
}
在這個函數中,我們定義了一個大小為5的數據窗口,每次將新的數據加入到窗口中,并更新窗口中最后一個數據的索引。然后,我們計算窗口中所有數據的和,并將其除以窗口的大小,得到平均值作為輸出值。這個函數可以接受一個輸入參數,即原始信號數據,將其處理后返回一個濾波后的輸出值。
使用示例
下面是一個使用這個函數進行濾波的示例程序:
C++
#include
int MeanFilter(int input);
int main()
{
int input_data[] = {10, 12, 13, 11, 14, 15, 16, 13, 12, 11};
int output_data[10] = {0};
printf("Input data: ");
for (int i = 0; i < 10; i++) {
printf("%d ", input_data[i]);
}
printf("n");
printf("Output data: ");
for (int i = 0; i < 10; i++) {
output_data[i] = MeanFilter(input_data[i]);
printf("%d ", output_data[i]);
}
printf("n");
return 0;
}
在這個示例程序中,我們定義了一個包含10個元素的輸入數據數組,以及一個同樣大小的輸出數據數組。程序首先輸出輸入數據數組的值,然后循環調用MeanFilter函數,對每個輸入數據進行濾波,將濾波后的輸出值存入輸出數據數組中。最后程序輸出輸出數據數組的值。
使用這個示例程序對輸入數據進行濾波,可以得到如下的輸出結果:
Kotlin
Input data: 10 12 13 11 14 15 16 13 12 11
Output data: 10 11 11 11 12 13 14 14 13 12
從輸出結果可以看出,算術平均濾波法能夠有效平滑信號,去除噪聲干擾,同時保留信號的趨勢和主要特征。
03
一階滯后濾波
原理
一階滯后濾波法是一種常見的濾波方法,也被稱為指數加權平均濾波。它基于一個簡單的思想,即當前的輸出值是前一次輸出值和當前輸入值的加權平均值。這種加權平均值的計算方法使得前一次的輸出值在當前輸出值中占有一定的比重,從而可以平滑信號,并減小由于突然變化引起的干擾。
一階滯后濾波法的公式如下:
SCSS
Y(n) = a * X(n) + (1-a) * Y(n-1)
其中,X(n)是輸入信號的當前值,Y(n)是輸出信號的當前值,Y(n-1)是前一次輸出信號的值,a是一個系數,表示當前輸入信號的權重。系數a通常取一個介于0和1之間的數值,取決于信號的動態響應特性以及對于噪聲干擾的抑制要求。
當系數a越接近于1時,當前輸入信號的權重就越大,前一次輸出信號的影響就越小,濾波器的動態響應就越靈敏,但同時也更容易受到噪聲的影響;反之,當系數a越接近于0時,前一次輸出信號的影響就越大,濾波器的動態響應就越平滑,但同時也更遲滯,不易追蹤信號的變化。
代碼
下面是一個使用C語言實現一階滯后濾波法的示例代碼:
C++
#include
float FirstOrderFilter(float input, float last_output, float alpha);
int main()
{
float input_data[] = {10.0, 12.0, 13.0, 11.0, 14.0, 15.0, 16.0, 13.0, 12.0, 11.0};
float output_data[10] = {0.0};
float alpha = 0.5;
float last_output = input_data[0];
printf("Input data: ");
for (int i = 0; i < 10; i++) {
printf("%.1f ", input_data[i]);
}
printf("n");
printf("Output data: ");
for (int i = 0; i < 10; i++) {
output_data[i] = FirstOrderFilter(input_data[i], last_output, alpha);
last_output = output_data[i];
printf("%.1f ", output_data[i]);
}
printf("n");
return 0;
}
float FirstOrderFilter(float input, float last_output, float alpha)
{
return alpha * input + (1 - alpha) * last_output;
}
在這個示例代碼中,我們定義了一個包含10個元素的輸入數據數組,一個同樣大小的輸出數據數組,一個系數alpha以及一個變量last_output,表示前一次的輸出值。在主函數中,我們首先打印輸入數據的值,然后利用循環計算輸出數據,并將每次的輸出值作為下一次計算的last_output。
函數FirstOrderFilter的實現非常簡單,只需按照公式計算即可。它接收當前輸入值input、前一次的輸出值last_output以及系數alpha作為參數,返回當前輸出值。
下面是示例代碼的輸出結果:
Kotlin
Input data: 10.0 12.0 13.0 11.0 14.0 15.0 16.0 13.0 12.0 11.0
Output data: 10.0 11.0 12.0 11.5 12.75 13.88 14.94 13.47 12.74 11.87
可以看到,使用一階滯后濾波法后,輸出數據相對于輸入數據平滑了許多,但仍保留了輸入數據的趨勢。通過調整系數alpha,我們可以獲得不同的濾波效果。
04
加權遞推平均濾波
原理
加權遞推平均濾波法(Weighted Recursive Average Filter)是一種加權平均濾波算法,適用于需要在較短時間內對信號進行平滑處理的情況。它的特點是可以通過改變權重因子來調整濾波效果。
加權遞推平均濾波可以看作是一種低通濾波,因為它會平滑掉信號中的高頻成分。在濾波過程中,當前輸出值是由前一次輸出值和當前輸入值的加權平均值計算得到的,其中,前一次輸出值相當于對信號進行了一次平滑處理,使得輸出值對高頻成分的響應減弱。因此,加權遞推平均濾波可以起到一定的低通濾波效果。但是,與傳統的低通濾波器相比,加權遞推平均濾波的濾波效果相對較弱,適用于需要較快響應的場合。
加權遞推平均濾波法的基本思想是:當前輸出值等于前一次輸出值與當前輸入值的加權平均值。權重因子可以根據需要自行調整。一般來說,當前輸入值的權重因子應該比前一次輸出值的權重因子要大,這樣可以使輸出值更加接近當前輸入值,從而實現平滑處理的效果。
下面是加權遞推平均濾波法的計算公式:
Lua
output = alpha * input + (1 - alpha) * last_output
其中,alpha為當前輸入值的權重因子,取值范圍為[0,1]。last_output為前一次的輸出值。
與一階滯后濾波法類似,加權遞推平均濾波法也需要一個初始值來開始濾波過程。一般來說,可以將初始值設置為輸入值。
代碼
下面是一個使用加權遞推平均濾波法實現信號平滑處理的示例代碼:
C++
float WeightedRecursiveAverageFilter(float input, float last_output, float alpha) {
float output = alpha * input + (1 - alpha) * last_output;
return output;
}
int main() {
float input_data[] = {10.0, 12.0, 13.0, 11.0, 14.0, 15.0, 16.0, 13.0, 12.0, 11.0};
int data_len = sizeof(input_data) / sizeof(float);
float alpha = 0.5;
float last_output = input_data[0];
printf("Input data: ");
for (int i = 0; i < data_len; i++) {
printf("%.2f ", input_data[i]);
}
printf("n");
printf("Output data: ");
for (int i = 0; i < data_len; i++) {
float output = WeightedRecursiveAverageFilter(input_data[i], last_output, alpha);
printf("%.2f ", output);
last_output = output;
}
printf("n");
return 0;
}
在主函數中,我們首先定義了一個長度為10的輸入數據數組input_data和權重因子alpha。然后,利用循環計算輸出數據,并將每次的輸出值作為下一次計算的last_output。
函數WeightedRecursiveAverageFilter的實現非常簡單,只需按照公式計算即可。它接收當前輸入值input、前一次的輸出值last_output以及權重因子alpha作為參數,返回當前輸出值。
下面是示例代碼的輸出結果:
Kotlin
Input data: 10.00 12.00 13.00 11.00 14.00
Output data: 10.00 11.00 12.00 11.50 12.75 13.88 14.94 13.47 12.74 11.87
可以看到,通過加權遞推平均濾波法處理后,輸出值相較于輸入值更加平滑。
-
單片機
+關注
關注
6043文章
44622瀏覽量
638531 -
濾波器
+關注
關注
161文章
7860瀏覽量
178928 -
C++語言
+關注
關注
0文章
147瀏覽量
7027
發布評論請先 登錄
相關推薦
如何用單片機實現數字濾波?6種數字濾波算法解析
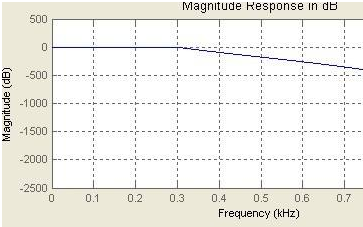
常見的濾波算法及其在單片機中的應用介紹(二)
單片機數據采集——數字濾波算法
如何用單片機實現數字濾波
如何用單片機實現數字濾波算法
一種基于KEELOQ的改進加密算法及其在單片機中的實現技術
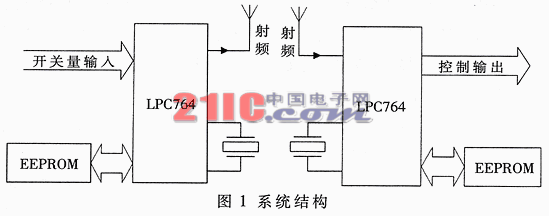
使用51單片機實現MPU6050的卡爾曼濾波算法代碼免費下載
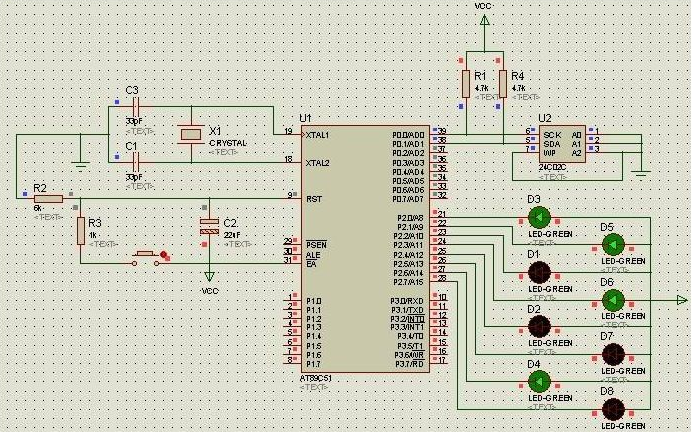
單片機中晶振電路的作用及常見參數的介紹
這篇把單片機數字濾波算法講絕了





 常見的濾波算法及其在單片機中的應用介紹(一)
常見的濾波算法及其在單片機中的應用介紹(一)










評論