在穩態部分的分析中,我們詳細地推演了電子電流、空穴電流、總電流以及各電壓構成部分與多余載流子濃度分布之間的關系,即一維空間的物理關系。
接下來,我們引入時間變量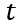 ,進入瞬態部分的分析。
,進入瞬態部分的分析。
當外部柵極控制電壓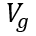 降低到閾值電壓
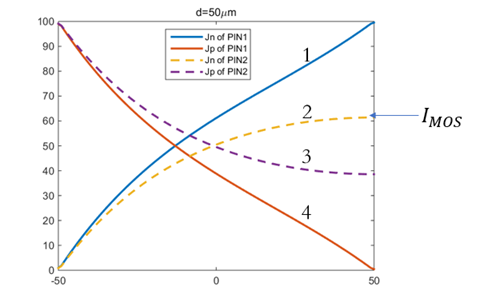
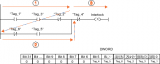
降低到閾值電壓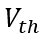 以下時,MOS部分的溝道立即閘斷,相應的電子電流變為0,借鑒《電流與電荷分布的初步分析1》中的插圖,即圖中
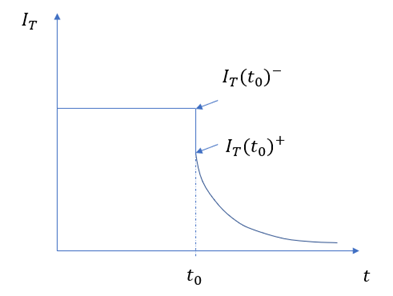
以下時,MOS部分的溝道立即閘斷,相應的電子電流變為0,借鑒《電流與電荷分布的初步分析1》中的插圖,即圖中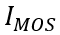 瞬間衰減為0,那么總電流就只剩下如圖2、3、4三個部分。
瞬間衰減為0,那么總電流就只剩下如圖2、3、4三個部分。
假設這個變化的時間為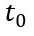 ,變化前后的總電流記為
,變化前后的總電流記為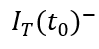 和
和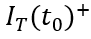 ,描繪總電流在
,描繪總電流在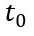 時刻發生突變。
時刻發生突變。
顯然, 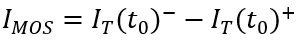 ,下一節我們會具體地討論
,下一節我們會具體地討論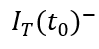 和
和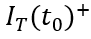 的關系。
的關系。
推演電流和電壓隨時間的變化關系的大致邏輯是:電流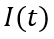 是器件內部電荷總量
是器件內部電荷總量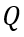 在時間維度為微分
在時間維度為微分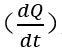 ,電荷總量
,電荷總量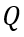 是載流子
是載流子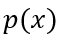 的積分,
的積分,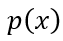 可以通過連續方程求解得出,其邊界條件為非耗盡區兩端的電荷濃度,即
可以通過連續方程求解得出,其邊界條件為非耗盡區兩端的電荷濃度,即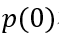 和
和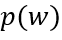 ,求解方法參考前面穩態部分。
,求解方法參考前面穩態部分。
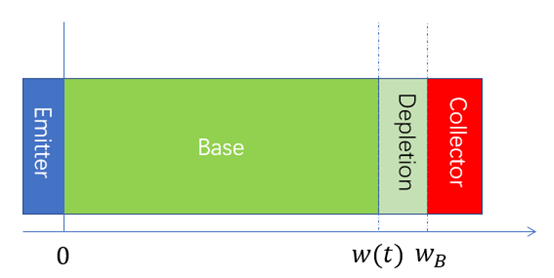
與穩態部分不同的是,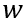 隨時間變化,記為
隨時間變化,記為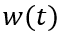
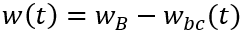 ,其中
,其中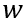 是base區寬度,
是base區寬度, 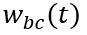 是耗盡區寬度;
是耗盡區寬度;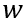 是固定值,
是固定值,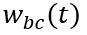 隨外加電壓
隨外加電壓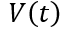 變化,根據泊松方程,
變化,根據泊松方程,
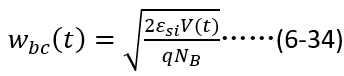
由此,根據穩態部分的邊界條件,我們就可以準確地推演出關斷瞬態過程中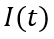 和
和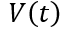 的關系。下面,我們根據上述邏輯,逐步展開分析,首先看電荷總量
的關系。下面,我們根據上述邏輯,逐步展開分析,首先看電荷總量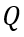 隨時間的變化。
隨時間的變化。
假設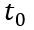 時刻為0時刻,先求解
時刻為0時刻,先求解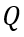 的初始值
的初始值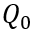 ,這可以通過對穩態下
,這可以通過對穩態下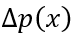 的積分得到,即對(6-10)進行積分,
的積分得到,即對(6-10)進行積分,
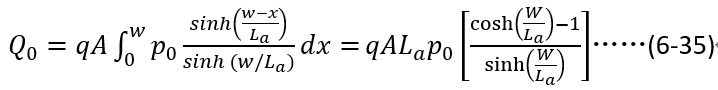
其中,A為芯片面積。分子利用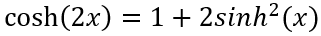 ,分母利用關系
,分母利用關系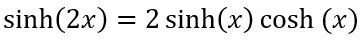 ,(6-35)可以進一步簡化為,
,(6-35)可以進一步簡化為,
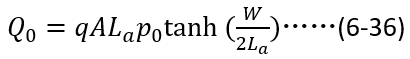
接下來,我們建立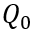 與電流初始條件
與電流初始條件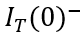 之間的關系,根據(6-36),即要建立
之間的關系,根據(6-36),即要建立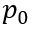 與
與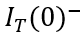 之間關系。
之間關系。
在穩態分析中,我們分別基于PIN模型和BJT模型建立了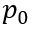 和電流密度
和電流密度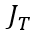 之間的關系(
之間的關系( 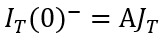 ),這里應該使用哪一個模型的結論呢?如穩態部分所分析,這取決于
),這里應該使用哪一個模型的結論呢?如穩態部分所分析,這取決于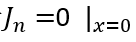 還是
還是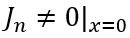 ,而這又取決于電子的載流子壽命,及其對應的擴散長度。
,而這又取決于電子的載流子壽命,及其對應的擴散長度。
當擴散長度大于BJT的基區寬度時,那么電子可以擴散到BJT的發射極,那么顯然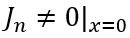 ,應采用BJT模型的結論;反之,電子無法擴散到BJT的發射極,那么
,應采用BJT模型的結論;反之,電子無法擴散到BJT的發射極,那么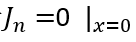 ,應采用PIN模型的結論。
,應采用PIN模型的結論。
為簡化后面的運算,這里我們采用基于PIN模型的結論(采用BJT模型也可以,但是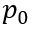 和電流密度
和電流密度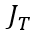 之間的關系就需要通過求解(6-21)來得到,相對復雜,但邏輯相同),即(6-11)所描述的
之間的關系就需要通過求解(6-21)來得到,相對復雜,但邏輯相同),即(6-11)所描述的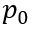 和電流密度
和電流密度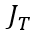 之間的關系,再乘以芯片面積:
之間的關系,再乘以芯片面積:
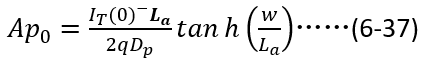
將(6-37)帶入(6-36),即可得到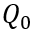 與電流初始條件
與電流初始條件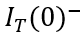 之間的關系,并化簡,
之間的關系,并化簡,
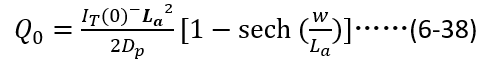
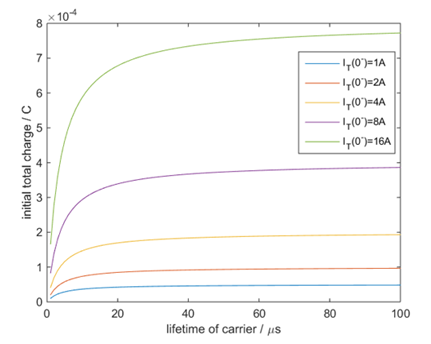
根據(6-38),我們看看初始電荷總量隨穩態電流以及載流子壽命之間的變化關系。顯然,在穩態電流值確定的情況下,初始電荷總量隨載流子壽命增加而趨向飽和。
-
IGBT
+關注
關注
1269文章
3834瀏覽量
250082 -
MOS
+關注
關注
32文章
1283瀏覽量
94314 -
BJT
+關注
關注
0文章
237瀏覽量
18243 -
載流子
+關注
關注
0文章
134瀏覽量
7693 -
閾值電壓
+關注
關注
0文章
73瀏覽量
51515
發布評論請先 登錄
相關推薦
抑制初始值的警告
換路定律及初始值的確定
淺析MCU內部的RAM上電之后的初始值相關問題
教你們怎么去設定寄存器的初始值

如何保證MCU上電后RAM的初始值唯一

如何保證MCU上電后RAM的初始值唯一

關于對IGBT關斷過程的分析





 IGBT的關斷瞬態分析—電荷存儲初始值
IGBT的關斷瞬態分析—電荷存儲初始值

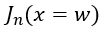
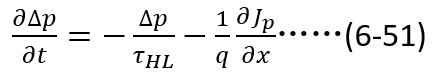











評論