前幾期文章介紹了整數槽繞組的磁勢。通過講解我們了解到，繞組的磁勢除了基波外還包括了一系列諧波，那么這些諧波磁勢產生的原因是什么？機理如何？這些諧波的大小又與哪些因素有關？如何才能削弱甚至消除這些諧波呢？接下來的兩期，就把這些問題掰開了揉碎了詳細分析一下。本期先講磁勢諧波產生的原因和機理。

1 繞組的電流層分布與磁勢

1.1 相關概念

繞組的磁勢是繞組的導體中通以電流而產生的，因此繞組的磁勢分布取決于導體電流的分布。電機繞組是由一些沿氣隙圓周分布的導體以某種方式連接而成的。當繞組中通以電流時，沿氣隙圓周就出現了一個“電流層”，這個電流層中各點的電流分布情況就決定了磁勢波的分布。為了描述這個電流層的電流分布情況，我們引入一個新概念——“電流線密度”或稱“安導強度”。定義氣隙圓周某點處單位弧度上的電流總和為電流層在該點的“電流線密度”或“安導強度”。根據這個定義，如果是單層繞組，設氣隙圓周上某一槽口寬度為θ(弧度)，θ=2π?[槽口寬度(米)/氣隙圓周長]，槽內嵌有N根導體，每根導體中的電流i(安)，假定電流均勻分布于槽口上，則該處氣隙圓周在整個槽口寬度θ范圍的電流線密度為A=(i?N)/θ(安/弧度)，由于i?N的意義為安培乘以導體數，簡稱“安導”，因此有些文獻和著作中也把“電流線密度”稱為“安導強度”。如果是雙層繞組，則i?N應為上、下層安導的代數和(上、下層電流方向相同時相加，否則相減)。由于齒頂范圍內無導體，因此在齒頂范圍內的安導強度應為零。由于不同槽內的導體可能分屬于不同的相，在同一時刻不同的槽內導體中電流就不同，所以氣隙圓周不同位置處的安導強度也不同，也就是說安導強度是沿氣隙圓周分布的空間函數，因此把安導強度在整個氣隙圓周上的分布稱為“安導強度分布波”，簡稱“安導波”，它是一個空間函數，用A(x)來表示，其中變量x表示氣隙圓周不同位置與坐標原點之間的弧度，單位是弧度，全圓周是2π。

以上是基于槽內安導均勻分布在槽口寬度范圍內的情況，如果認為槽內的安導i?N，不是均勻分布于整個槽口寬度上，而是集中在槽口正中一點上，則θ→0而A→∞。這時每個槽產生的安導波變成一個沖激函數(數學中的δ—函數)，在槽口正中一點A=∞，而在其他各點A=0，且該函數沿氣隙圓周在一齒距范圍內的積分等于槽內的安導i?N。

小結一下：如果認為槽內安導均勻分布在槽口寬度范圍內，則安導波A(x)就是沿氣隙圓周分布的一系列矩形脈沖波，每個脈沖寬度為一個槽口的弧度范圍，在該范圍的函數值為A=(i?N)/θ (安/弧度)，每個齒頂范圍的函數值為0；如果認為槽內安導集中在槽口中心一點，則安導波A(x)就是沿氣隙圓周分布的一系列沖激函數，每個槽口中心的函數值為∞，其余范圍函數值為0，函數在每個齒距范圍的積分為該槽內安導。

這個“安導波”看起來與電機設計中的線負荷有些類似，它們都是反映氣隙圓周上電流分布強度的物理量，但二者有著本質的區別：線負荷A是指電樞圓周上單位弧長上的電流，即A=∑(I?N)/C，其中：I為每根導體中的電流有效值；N為導體數；C為電樞圓周的周長，也就是說，線負荷是指氣隙圓周上所有導體中的電流有效值之和(不考慮電流的方向和相位)除以整個氣隙圓周的周長，單位是“安培/米”，對于一個特定的電機，當電樞電流一定時，線負荷就是一個定值，它反映了電機在某種負載條件下氣隙圓周上電流層總的分布強度，從某種程度上代表了電樞表面的銅耗和電樞反應的強弱，因此電機的熱負荷和電樞反應電抗等與線負荷有密切關系，是電機設計過程中的一個重要參數；而“安導波”A(x)是指電樞圓周某處單位弧度上的電流，它是一個空間函數，而不是一個定值。單位也與線負荷不同，安導波的單位是“安培/弧度”。安導波里的電流是指該處導體中電流的瞬時值，在任意固定時刻，由于交流繞組中各槽內導體的電流瞬時值不同，所以氣隙圓周上各處安導強度也不同，因此“安導波”不是一個定值，而是一個沿氣隙圓周分布的空間分布函數，代表了某時刻氣隙圓周上不同位置處的電流分布強度。如果再考慮繞組中的電流為交流電流，則安導波還是時間的函數。由于這里我們只分析磁勢的空間分布特征和空間諧波，因此可把時間設定為某一個特定時刻(t=t0時刻)，分析該特定時刻的安導波和磁勢波，此時安導波和磁勢波就僅是空間的函數。

1.2 安導波與繞組磁勢的關系

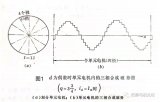
根據上述安導波的定義可知，安導波沿氣隙圓周某一段的積分等于該段弧上的凈有總安導，即該段上所有各槽安導的代數和。取氣隙圓周上磁場強度為零的一點作為坐標原點，通過坐標原點和坐標為x的任意一點取一閉合回路，如圖1虛線所示。

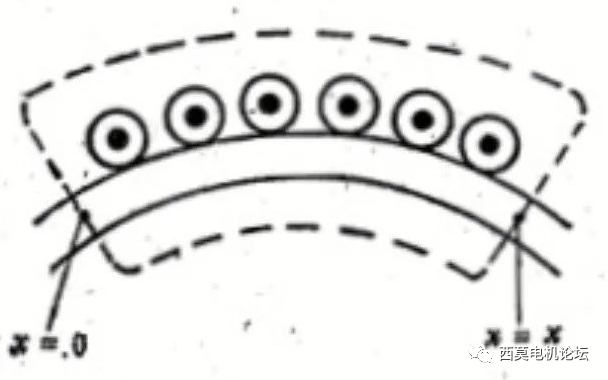
圖1磁勢和安導的關系

則由全電流定律，沿閉合回路的總磁壓降應等于回路內的總電流，即安導波沿弧段【0～x】范圍的積分 ∫【0～x】A(x)dx。由于x=0點的磁場強度為零，因此該點的氣隙磁壓降為零，于是，在假定鐵心的相對磁導率為無窮大，因而鐵心中的磁壓降可以忽略的條件下，閉合回路的總壓降就等于x=x點處氣隙的磁壓降，稱為x點的磁勢，用符號F(x)表示。這樣可得磁勢波F(x)和安導波A(x)之間的關系為：

F(x)=∫【0～x】A(x)dx⑴

上述分析中，是假定坐標原點的磁場強度為0的條件下給出的。由全電流定律可知，式⑴中的F(x)是相對于坐標原點的磁勢，如果坐標原點磁場強度不為0，則還需要在式⑴的右側加上x=0點的氣隙磁壓降才是x=x點的磁勢絕對值。顯然這并不改變整個磁勢曲線的形狀，只不過整個曲線向上或向下平移了一段距離而已。由于曲線形狀不變時，曲線所包含的諧波成分不變，因此從諧波分析的觀點看，坐標原點可以任意選取。

2 交流繞組磁勢諧波產生的原因

2.1 產生正弦波磁勢的條件

以上分析可知，當多相繞組通以多相電流時，在氣隙中產生的磁勢波由⑴式決定，為電流層中安導波的積分。由⑴式可見，欲使磁勢波為正弦，則安導波的波形必須為正弦，而要想使安導波為正弦，則必須使氣隙中每增加一個任意小的Δx，安導數都必須按照正弦(或余弦)的規律遞增一個sin(x+Δx)-sin(x)，這意味著任意小的Δx內必須要有一個槽存在(有導體存在)，而且相鄰兩個槽中的安導數都不同，導體中的電流按照正弦規律變化。那么這將是一個什么樣的繞組？通什么樣的電流呢？首先任意小的Δx范圍內都必須要存在一個槽，就意味著要有無窮多個槽，而無窮多個槽也就是沒有了齒槽；其次任意兩個相鄰槽內導體的電流都不同則意味著在一對極距的范圍內，每個槽內的電流相位都不同，即每個槽都屬于不同的相，也就是說繞組的相數也是無窮多。這樣在無窮多相繞組中通以無窮多相對稱電流即可得到純正弦波磁勢。

小結一下：產生純正弦波磁勢的充要條件，一是槽數無窮多；二是相數無窮多；三是在這樣的無窮多相繞組中，通以無窮多相的對稱電流。滿足上述三個條件就能產生正弦波磁勢。顯然這是一個理想的繞組，無窮多相電源也是一種理想電源。在實際的電機中通常是將繞組嵌放在有限的槽內，而且相數也是有限的，電源也不可能做到無窮多相。雖然也有些電機是無槽電機，但這并不能保證所有導體都是獨立均勻布置在整個氣隙中，至少導體還是有一定的粗細，線徑不是無窮小，因此導體的分布仍然是離散的，至于繞組相數和電源相數則更不可能是無窮多。因此這種理想也只能是一個理想，實際電機中不可能實現，隨之繞組的電勢成為純正弦也就變成了一種純粹的理想。

2.2 多相繞組的合成磁勢波

既然實際電機是在有限槽數內布置有限相繞組，那么它產生的繞組磁勢必然不是純正弦，不是純正弦又會是什么樣子的呢？

當多相繞組中所通的電流已知時，氣隙圓周上的安導波即已知，根據式⑴就可以得到多相繞組的合成磁勢波形圖。

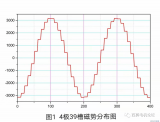
以三相對稱單層繞組為例，繞組的參數為：三相、2極、12槽，q=2、Y=τ=6。假設每個槽內的安導集中分布在槽口中心一點，則根據式⑴，每過一個槽中心點，磁勢就會跳變一個臺階，臺階的高度等于該槽內的安導代數和，臺階向上跳變還是向下跳變則取決于該槽內安導代數和的正負，正則向上跳變，負則向下跳變。這樣就得到了三相繞組的合成磁勢波形圖，如圖2所示。這是在A相繞組電流達到峰值時刻的繞組磁勢波形圖，需要順便說明的是，不同時刻合成磁勢的波形圖是不同的，但這并不影響磁勢的空間諧波次數和大小，對此將在下期詳細講解。

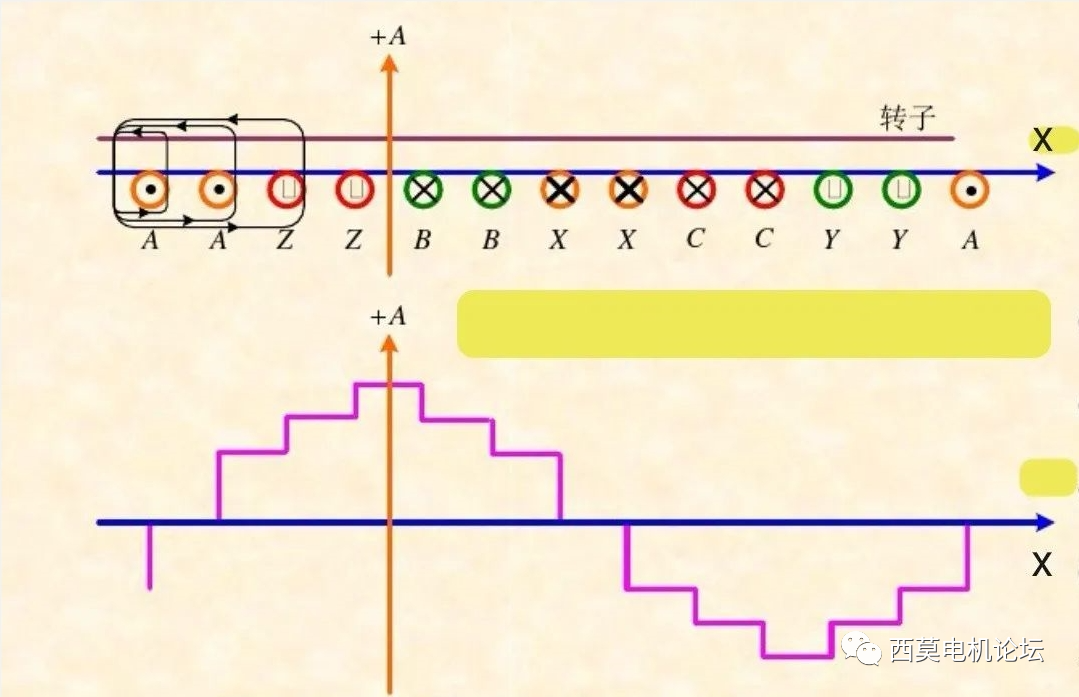
圖2 三相單層繞組的合成磁勢波

2p=2q=2m=3

由圖2可見，這個單層繞組產生的磁勢是一個階梯波。從這個階梯波上可以進一步看出：①每個極對數范圍內臺階的數量為每對極的槽數；②相鄰兩個臺階的高度并不是按照正弦規律變化的，而是在一個相帶(q個槽)的范圍內，臺階的高度相同，不同相帶的臺階高度不同。顯然這個梯形波與基波正弦曲線相比，存在著差別，所以說，這種梯形波除了存在基波外，還存在著一系列諧波，這個梯形波與純正的正弦基波之差就是這些諧波的總和，也正是由于上述兩個原因才導致了諧波磁勢的出現。對于第①個(階梯)原因引起的諧波，我們稱之為齒諧波；對于第②個(階梯高度不按正弦變化)原因引起的諧波，我們稱之為相帶諧波。

2.3 齒諧波和相帶諧波產生的機理

如前所述，根據產生磁勢諧波的原因不同，可以把磁勢諧波分為齒諧波和相帶諧波。接下來我們就進一步把齒諧波和相帶諧波分離，來看一看齒諧波和相帶諧波到底是個什么模樣。如圖3所示為把合成的階梯波磁勢進一步分解為齒諧波和相帶諧波的情況。

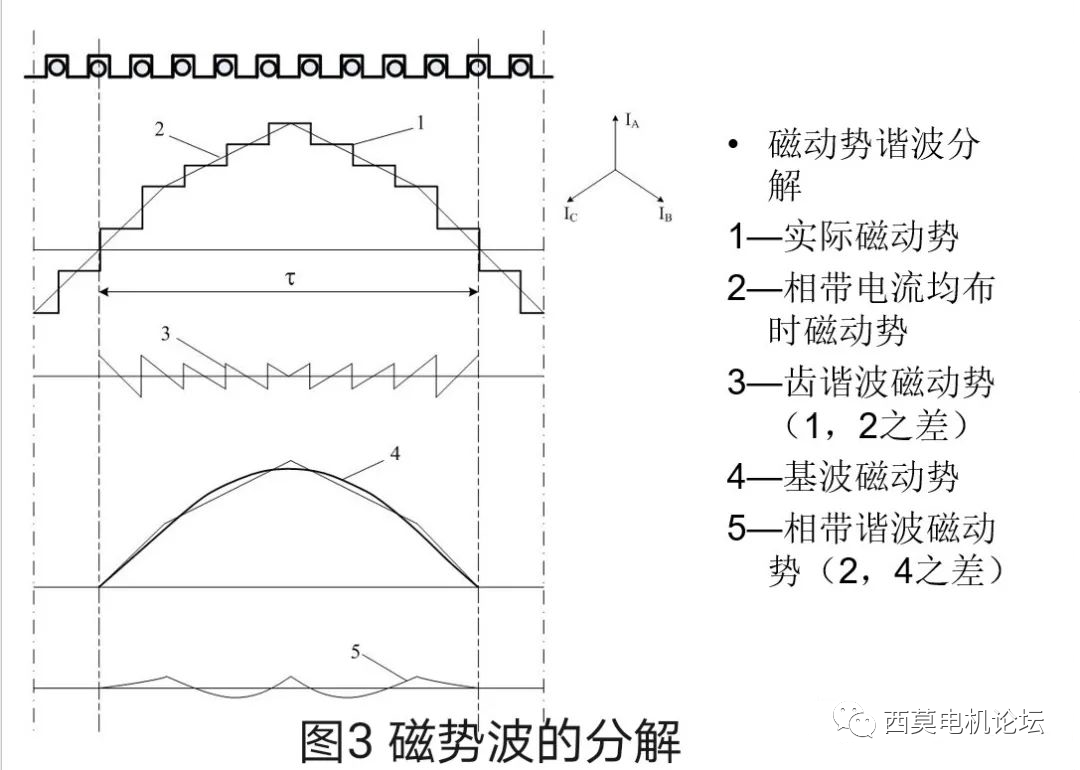
圖3中，曲線1為實際的合成磁勢波形，它就是圖2中所示的階梯波；曲線4為階梯狀合成磁勢的基波，它是一條純正弦曲線。曲線1包含了基波、齒諧波和相帶諧波，也就是說曲線1所示的階梯波是由基波、齒諧波和相帶諧波相加而成的。

先說齒諧波產生的機理。齒諧波是由于階梯的存在而產生的，而產生階梯的原因是由于定子開有齒槽引起的，因此稱其為齒諧波。當定子開有有限個齒槽時，安導波分布就不是連續的，而是集中在槽口中心點呈離散分布，從而使磁勢產生階梯。如果我們把槽數逐步增加，則階梯個數就會隨之增加，而相鄰兩槽產生的階梯高度則隨之變小，如果把槽數增加至無窮大，即q→∞，則階梯就會消失了，隨之齒諧波也就不復存在了，磁勢就變成了曲線2的形狀。

說完齒諧波再說相帶諧波產生的機理。雖然曲線2中不存在了階梯，也不存在了齒諧波，但由于相數仍然是有限的三相，在一個相帶范圍內，安導強度是相同的，而這個安導強度就代表了磁勢的變化斜率，因此在一個相帶范圍內磁勢增加的斜率是相同的，不同相帶范圍內由于安導強度不同而斜率也不同。正因如此，曲線2中存在著許多個折線段，折線段的數量取決于相帶數，在一對極范圍內，有多少個相帶，就有多少段折線，而折線段的斜率則取決于該相帶中的安導強度。曲線2這條折線，雖然不包含了齒諧波，諧波含量比梯形波小了許多，更接近了正弦基波，但它與正弦基波曲線相比仍然存在著差距，說明仍然存在著諧波，而這些諧波產生的原因是由于用折線逼近正弦曲線時，各段折線的斜率并不是完全按照正弦規律連續變化的，而是由于相帶的劃分而引起的各段折線斜率斷續所造成的，因此稱其為相帶諧波。

綜上所述，曲線2所示的折線已不包括齒諧波，但仍然包括相帶諧波，也就是說，曲線2是相帶諧波與基波之和。

如前所述，相帶諧波是由于相數有限而引起的，如果在無窮多個槽的基礎上逐步增加相數，則折線段的數量將隨之增多，相數增多后每個相帶的安導波都按正弦規律變化，則折線段的斜率也會按照正弦規律變化，這樣相數越多，折線的形狀就會越逼近基波正弦曲線，說明相數越多，相帶諧波含量就越小。如果把相數增加到無窮大，則折線就變成了基波正弦曲線4了，此時就即不存在齒諧波也不存在相帶諧波了。

歸納一下：

曲線1=基波+齒諧波加+相帶諧波⑵

曲線2=基波+相帶諧波⑶

曲線4=基波⑷

將⑵式減去⑶式得到曲線3，曲線3即為齒諧波曲線，即：

曲線1-曲線2=曲線3=齒諧波⑸

將⑶式減去⑷式得到曲線5，曲線5即為相帶諧波曲線，即：

曲線2-曲線4=曲線5=相帶諧波⑹

由圖3中的曲線3和曲線5可以看出齒諧波和相帶諧波的形狀。如果再進一步將曲線3和曲線5做傅立葉分解，就可以分別得到齒諧波和相帶諧波所包含的諧波分量（略）。從兩個曲線的形狀定性地分析，可以看出，齒諧波的波長主要取決于齒距，波長約一個齒距的(Z1/p)±1次諧波最強烈，其余波長更短的諧波次數為k?(Z1/p)±1次，這是齒諧波的重要特征。相帶諧波的波長主要取決于相帶的寬度，波長約為一個相帶寬度的2m±1次諧波最強烈，其余波長更短的諧波次數為2km±1次，這是相帶諧波的重要特征。

簡單總結一下齒諧波和相帶諧波的產生機理：齒諧波是由階梯引起，而階梯的產生是由于定子開槽使安導波不連續，只在槽口中心躍變導致；相帶諧波是由折線引起，而折線的產生是由于一個相帶內的安導強度相同，磁勢變化斜率相同導致。

本期介紹了繞組磁勢諧波產生的原因，分析了相帶諧波和齒諧波的產生機理，定性地分析了影響相帶諧波和齒諧波的因素，并定性分析了相帶諧波和齒諧波的基本特征。下期我們將繼續深入分析相帶諧波和齒諧波大小影響因素，并進一步講解抑制和消除磁勢諧波的方法及其機理。