機器學習模型依賴于批處理（Batching）來提高推斷吞吐量，尤其是對于 ResNet 和 DenseNet 等較小的計算機視覺模型。GPT 以及其他大型語言模型（Large Language Model, LLM）是當今最熱門的模型。批處理對于 GPT 和大語言模型仍然適用嗎？讓我們一探究竟。

背景知識

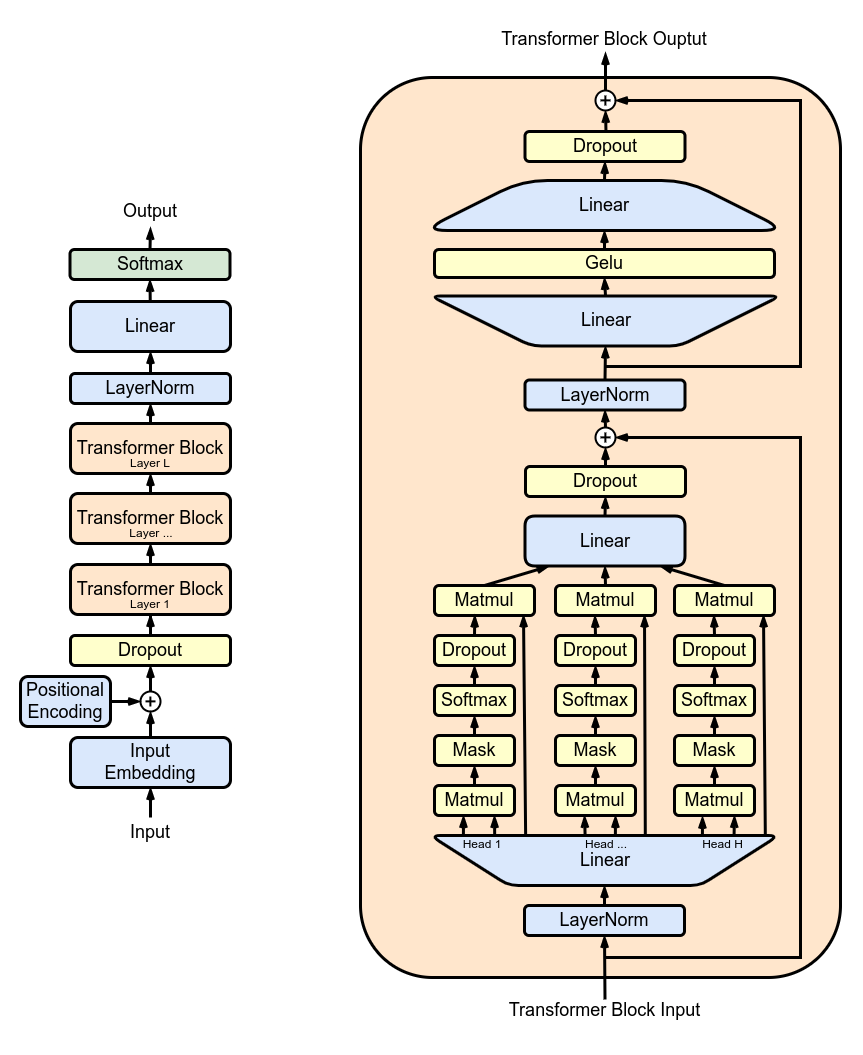
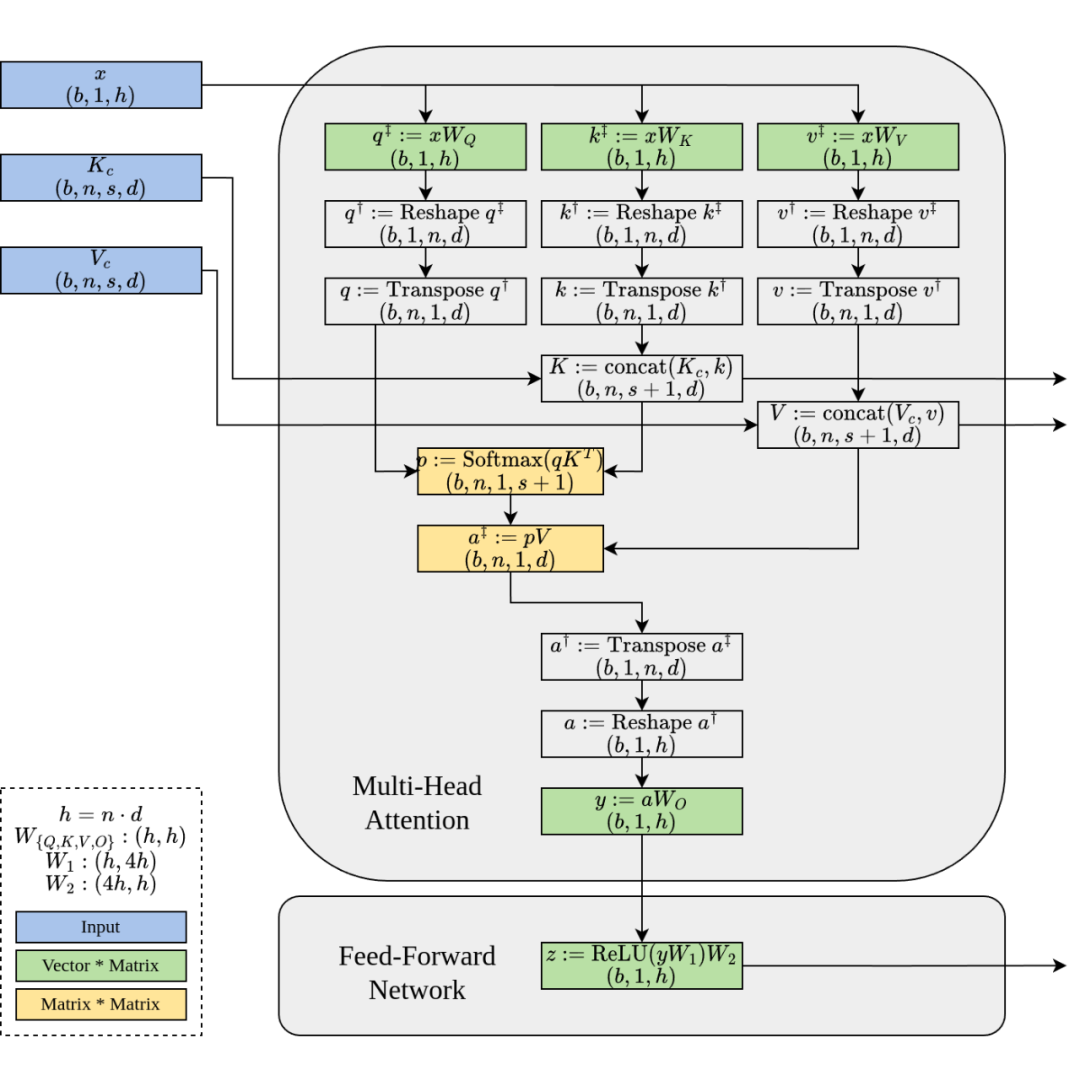
上圖來源于維基百科 [1]，展示了 GPT 的整體架構和一個 Transformer 層。讓我們簡化對 GPT 的理解。GPT本質上是一堆 Transformer 層的堆疊。由于每個 Transformer 層的架構相同，我們將重點放在單個 Transformer 層上。一個 Transformer 層包括三個部分：密集層投影（Dense Layer）、自注意力機制（Self-Attention）和前饋網絡（Feed-Forward-Network）（即兩個密集層）。

為簡單起見，我們將忽略與計算和輸入輸出相關的一些次要細節，如層歸一化（LayerNorm）、掩蔽層（Mask）、暫退層（Dropout）以及殘差連接（Residual Connection）。相反，我們將專注于分析矩陣乘法。如果你想更深入地了解 GPT 架構或自注意力機制，我建議閱讀本文末尾列出的論文和博客文章。

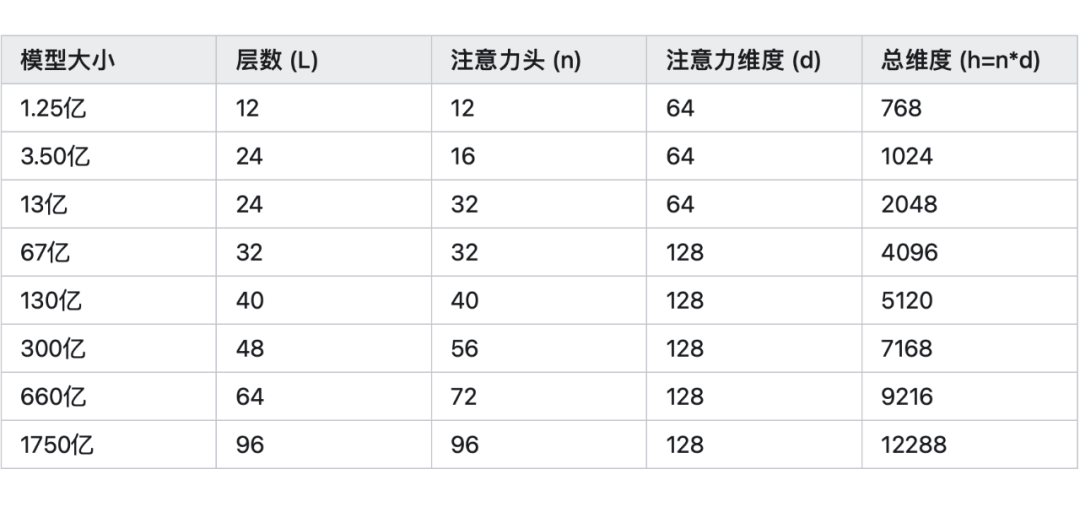
GPT 模型有不同的尺寸，參數數量從 1.25 億到 1750 億不等。下表概述了各種 GPT 模型尺寸的超參數。

使用 GPT 生成文本時，用戶向模型提供一個提示（prompt）。模型處理這個提示，生成第一個輸出詞元（Token）和兩個稱為 KV 緩存（KV Cache）的張量。我們稱之為初始階段（Initial Stage）。然后，模型將前一個輸出詞元和 KV 緩存作為輸入，生成下一個輸出詞元和更新后的 KV 緩存。我們稱之為自回歸（Auto-Regression）步驟。自回歸步驟不斷重復，直至模型生成完整的輸出。

計算步驟, FLOP, I/O

為了增強我們對 Transformer 層的理解，我創建了一個表格，按順序列出了計算步驟。我們可以從上到下閱讀這個表格，類似于執行程序。 除了提供了計算流程和輸出形狀（Shape），表格還提供了每個步驟的 FLOPs（浮點操作，即計算量）和 I/O 字節數（從 GPU 內存傳輸到 GPU 寄存器的數據傳輸）的數量。當將一個 NxM 矩陣與一個 MxP 矩陣相乘以產生一個 NxP 矩陣時，FLOP 計數為 N*M*P，I/O 計數為 N*M + M*P + N*P。此外，我們定義算術強度（Arithmetic Intensity）為 FLOP : I/O。

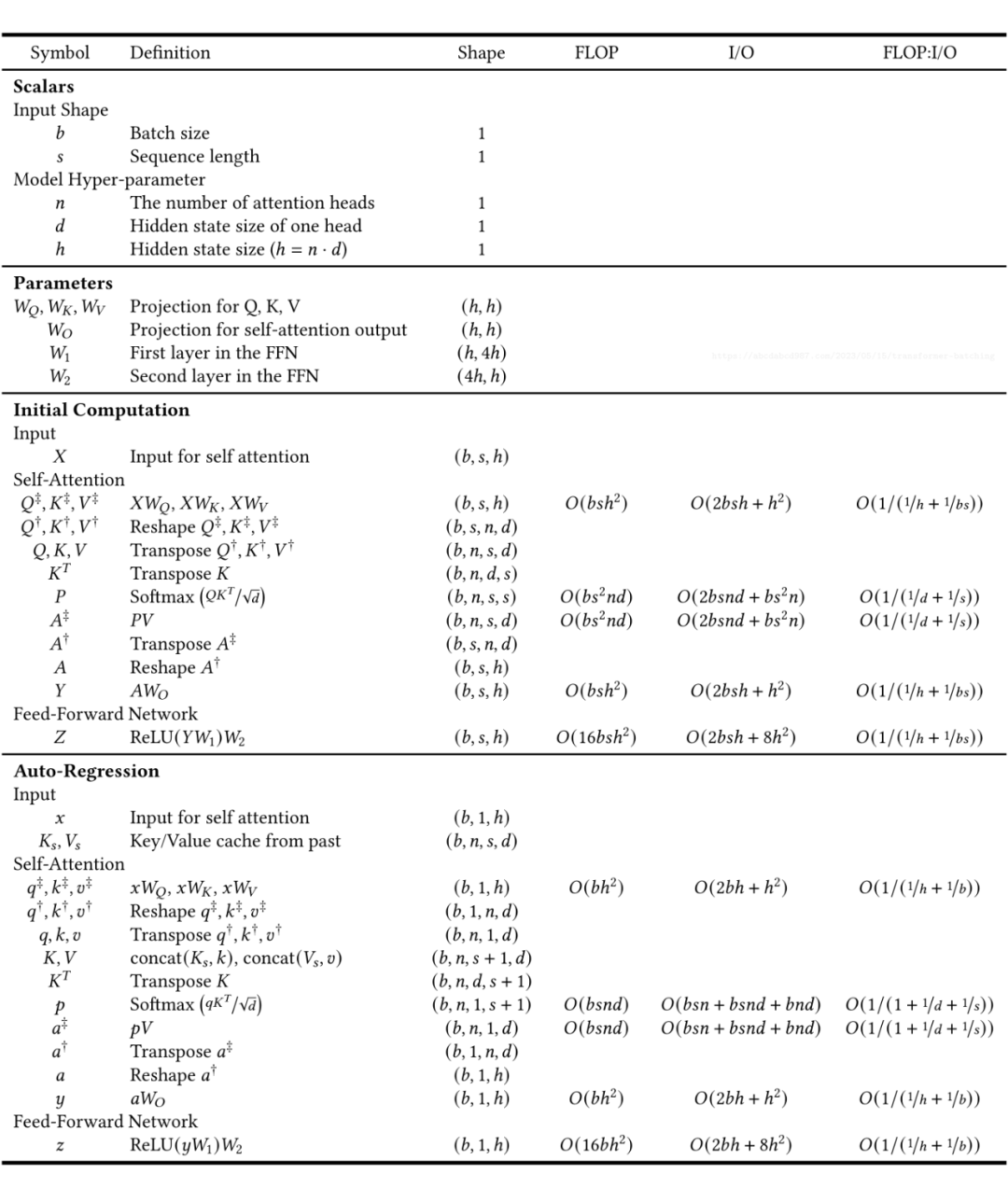
讓我們一起仔細研究這張表格。以下是我覺得一些有趣的點：

參數：

自注意力具有 3h^2 個參數，而前饋神經網絡（加上輸出投影（Output Projection））具有 9h^2 個參數。

自注意力僅占總模型參數的四分之一。

內存使用：

Softmax（QK^T）占用的內存為 n*s^2，這是大語言模型難以支持較長的文本長度的原因之一。舉個例子，67 億參數的模型具有 32 個注意力頭（Self-Attention Head），假設輸入有 16384 個詞元，那么我們需要 16 GB 的內存來存儲這個臨時值（32 * 16384^2 * sizeof（float16））。

相比之下，Softmax（QK^T）V 以及 Q，K，V 和其他隱藏狀態（Hidden States）只使用 n*d*s 內存。在前面的例子中，大小為 128MB（4096 * 16384 * sizeof（float16））。

K，V 需要保存下來以供后續自回歸使用。在前面的例子中，每層 KV 緩存占用 256 MB（128 MB * 2），67 億參數的模型有有 32 個 Transformer 層，那么總的 KV 緩存需要占用 8GB（256 MB * 32）顯存。

時間復雜度：

眾所周知，Transformer 時間復雜度與序列長度平方成正比，正如上表中表示 Q，K，V 的矩陣乘法的行所示。

更準確地說，考慮到密集層，初始階段的總時間復雜度為 O（s^2h + sh^2），自回歸階段為 O（sh + h^2）。

鑒于 h（>4096）通常比 s（<2048）大得多，可以說嵌入（Embedding）維度 h 的二次項比序列長度更影響時間復雜度。

矩陣乘法：

Transformer 層涉及兩種類型的矩陣乘法。

第一種類型是密集層：

密集層使用向量矩陣乘法將輸入向量轉換為另一個向量。

對于更高維度的輸入，向量矩陣乘法在除了最后一個維度之外的所有維度上進行廣播。例如，當將形狀為（h, h）的密集層應用于形狀為（b, s, h）的張量時，在矩陣乘法之前將張量重塑（Reshape）為（b*s, h），然后在之后重塑回（b, s, h）。

對于形狀為（(h, h）的密集層和形狀為（b, h）的批處理輸入，計算強度為 O（1 /（1+1/b））。增加批處理大小可以提高密集層的效率。

第二種類型是自注意力：

自注意力計算一個輸入序列中詞元之間的關系。

對于批處理輸入，Q 和 K 的形狀都為（b, n, s, d）。操作 QK^T 實際上是批處理矩陣乘法（Batched Matrix Multiplication）。對于批處理的第 i 個條目和第 j 個注意力頭（Self-Attention Head），結果 out[i, j] := matmul（Q[i, j, :, :], K[i, j, :, :].T）。隨著 b 的增加，計算和 I/O 需求都增加，使算術強度保持不變。

初始階段的批處理：

密集層：

由于序列長度這一維度的存在，即使批處理大小為 1，輸入也已經是批處理的。

因為序列長度通常很長，所以我們可以認為它已經很好地進行了批處理。

因此，在初始階段，批處理對密集層的效益不大。

自注意力：

正如前面提到的，批處理不會增加自注意力的算術強度。因此，在初始階段，批處理對自注意力并沒有幫助。（其實也不完全是這樣……我們會在下一個部分討論。）

自回歸階段的批處理：

密集層：

自回歸階段的密集層輸入的形狀為（b, 1, h）。

顯然這里批處理能帶來的大幅效率提升。

自注意力：

同理，批處理在這里并沒有什么作用。（其實也不完全是這樣……我們會在下一個部分討論。）

全程的批處理：

密集層和自注意力：

批處理有助于密集層，但對自注意力沒有幫助。

密集層占據了模型參數的 3/4，這表明密集層的執行時間占據了整個 Transformer 層執行時間的一大部分。

因此，批處理對整個模型的效益很大。

初始階段和自回歸：

初始階段已經在序列長度這一維度進行了很好的批處理，提升空間較小。而自回歸能從批處理中獲得很大的吞吐量提升。

自回歸步驟通常要執行非常多次，例如生成 100 個甚至 1000 個詞元。因此，自回歸比初始階段要花費更多時間。

因此，批處理能極大地提高端到端文本生成的效率。

微基準測試

我決定做一些微基準測試（Microbenchmark）來驗證我對密集層、自注意力、初始階段、以及自回歸階段中批處理效應的理解。

測試代碼大致如下：

defbench_dense(n,d,b,s):
h=n*d
X=torch.rand((b,s,h),dtype=torch.bfloat16,device="cuda")
W=torch.rand((h,h),dtype=torch.bfloat16,device="cuda")
defrun():
torch.matmul(X,W)
torch.cuda.synchronize()
latency=benchmark(run)

defbench_qk_init(n,d,b,s):
Q=torch.rand((b,n,s,d),dtype=torch.bfloat16,device="cuda")
K=torch.rand((b,n,s,d),dtype=torch.bfloat16,device="cuda")
defrun():
torch.bmm(Q.view(b*n,s,d),K.view(b*n,s,d).transpose(1,2))
torch.cuda.synchronize()
latency=benchmark(run)

defbench_qk_ar(n,d,b,s):
Q=torch.rand((b,n,1,d),dtype=torch.bfloat16,device="cuda")
K=torch.rand((b,n,s,d),dtype=torch.bfloat16,device="cuda")
defrun():
torch.bmm(Q.view(b*n,1,d),K.view(b*n,s,d).transpose(1,2))
torch.cuda.synchronize()
latency=benchmark(run)

我使用了 PyTorch 2.0，在 NVIDIA A100 上運行了這些基準測試。基準測試參數的范圍是：

h=[768,1024,2048,4096,5120,7168,9216,12288]
s=[1,10,20,50,100,200,500,1000,2000,5000]
b=[1,2,3,4,5,6,7,8,
10,12,14,16,20,24,28,32,
40,48,56,64,80,96,112,128]

3.1 整體批處理

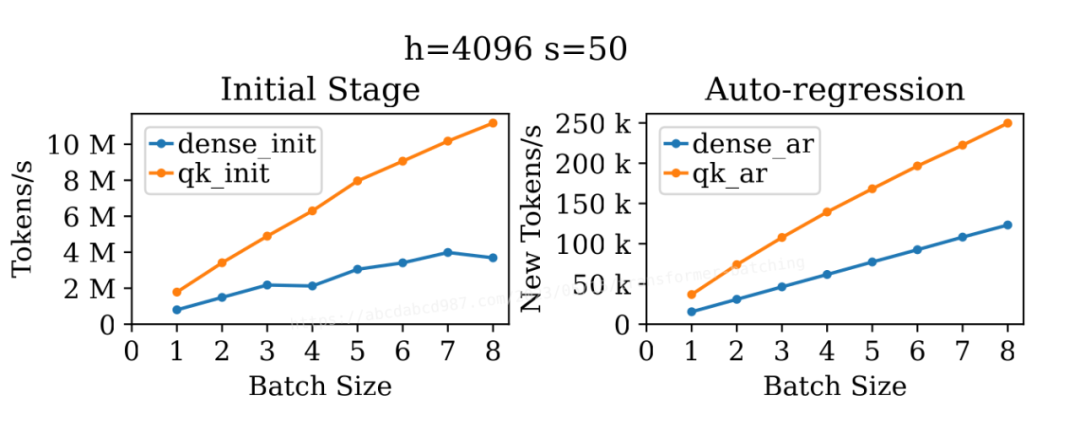
上圖展示了批處理大小對密集層和自注意力在初始階段和自回歸階段吞吐量的影響。出乎我的意料的是，這四條線都展現出了批處理對吞吐量的提升。

對于 dense_init，批處理的提升可能是因為序列長度較小（50）。A100 輕松處理了大小為 4096 × 4096 × 4096 的矩陣乘法，而批處理大小為 50 未能充分利用所有可用的計算單元。

那么，對于更長的序列長度呢？

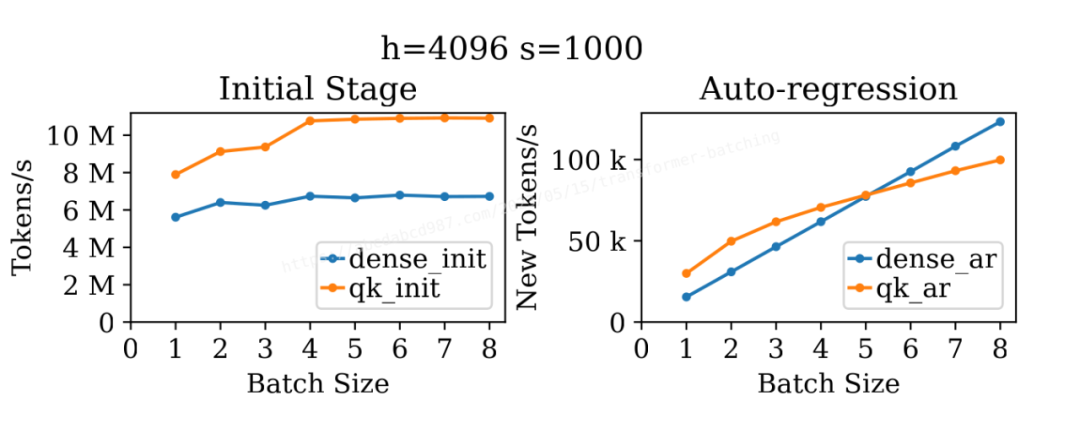
上圖展示了類似的結果，但序列長度為 1000。再次出乎我的意料的是，無論是 qk_init 還是 qk_ar 都在批處理中獲得了提升，尤其是在比較批處理大小為 1 和 4 時。可能的原因是，在并行運行 32*b 個這樣的矩陣乘法實例時，執行 1000×128×1000 的矩陣乘法實際上太容易了。另一個解釋可能是矩陣乘法核心不夠優化，未能充分利用可用的計算單元。

另一方面，由于序列長度已經很長，dense_init 不再從批處理中獲得吞吐量的提升。正如先前分析的那樣，在這個例子中 dense_ar 依然具有極佳的批處理效應。

3.2 密集層的批處理

讓我們更仔細地看看密集層。

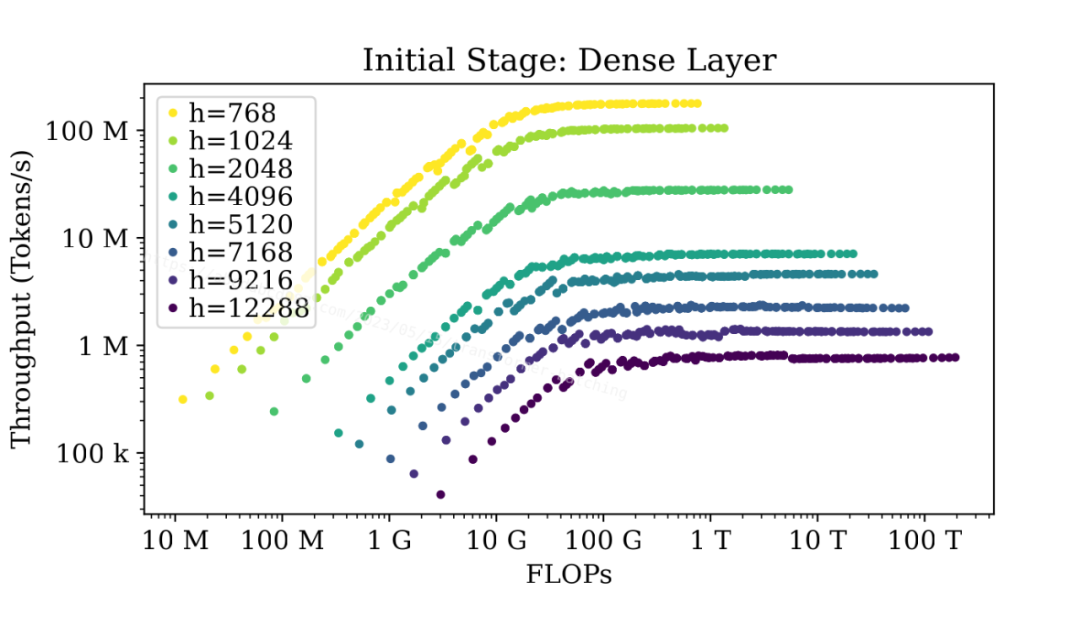
上圖顯示了不同大小的密集層的吞吐量與總浮點運算數（FLOPs）之間的關系。該圖使用 FLOPs 作為 x 軸，基本上等同于 b*s 相似，因為 FLOPs 是 O(bsh^2)。比起使用 b*s 作為 x 軸，使用 FLOPs 作為 x 軸可以更好地在同一張圖中區分不同的模型大小。

圖中顯示，無論模型有多大，當序列長度不大時，密集層在初始階段在達到最大吞吐量之前都可以在不同程度上受益于批處理。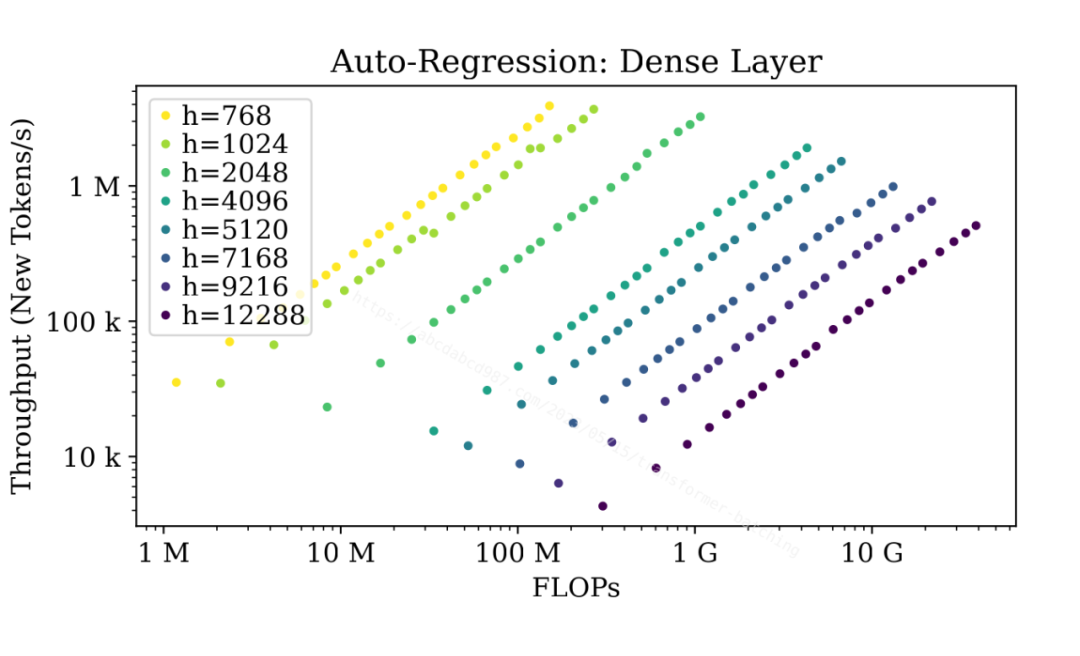



上圖顯示了自回歸階段。由于自回歸階段中的密集層序列長度始終為 1，批處理效應幾乎沒有上限。

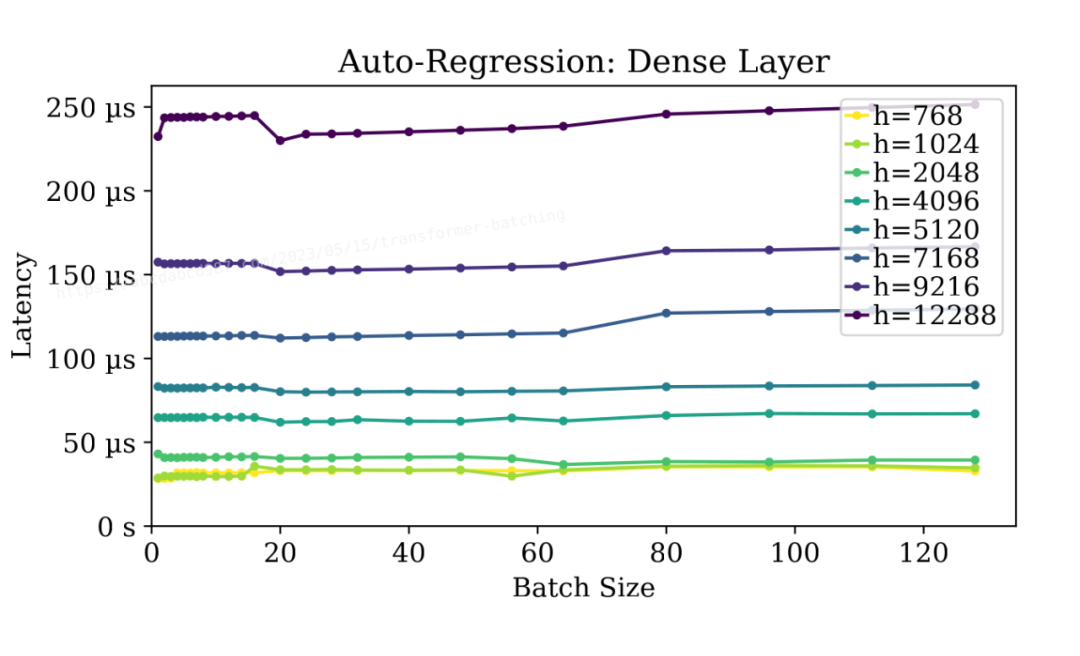
更好的是，如上圖所示，批處理自回歸階段的密集層不會對延遲產生顯著影響。批處理大小為128時，幾乎與無批處理時的延遲相當低。這簡直就是天上掉餡餅！

3.3 自注意力的批處理

現在，讓我們來看看自注意力。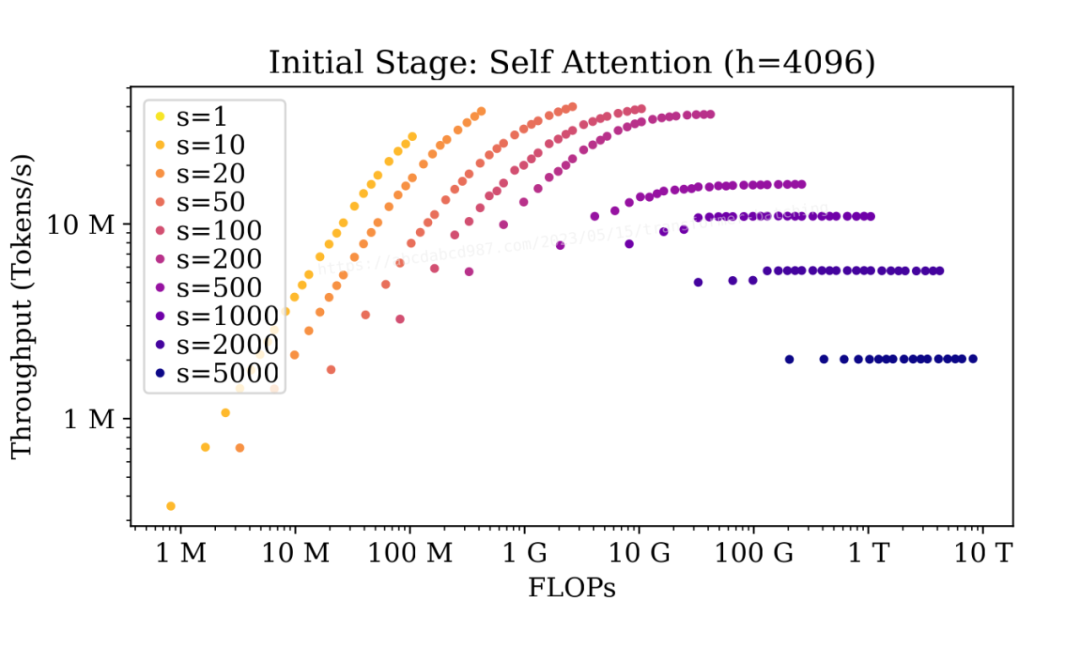



在初始階段，當序列長度較短（s<=100）時，批處理會產生顯著的影響，但對于較長的序列（s>=500），批處理的影響較小。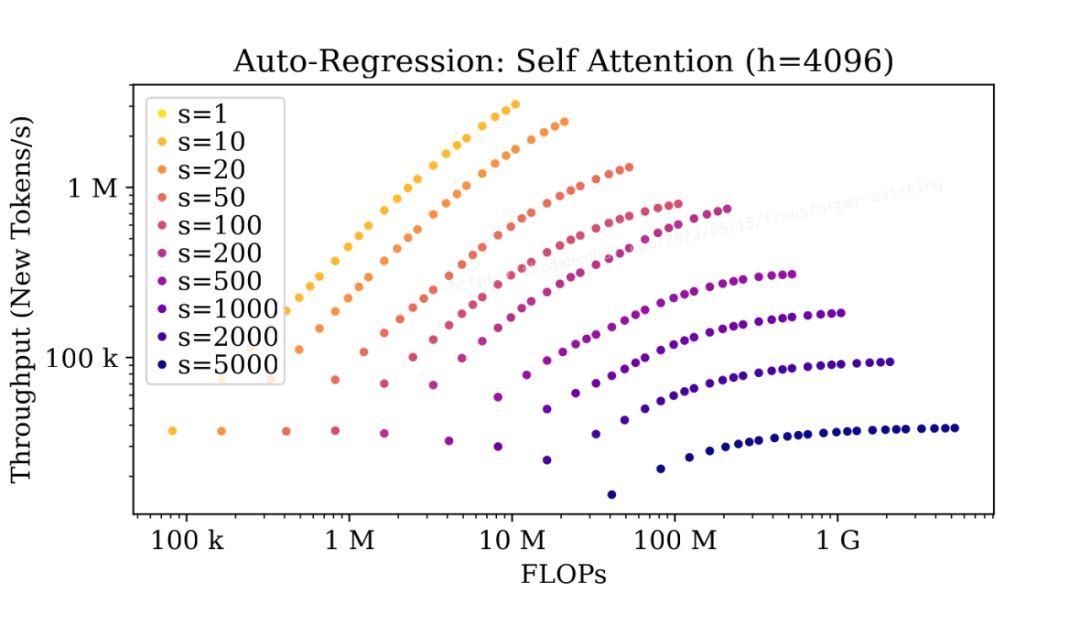



自回歸階段的情況類似，因為兩個階段中的自注意力具有相同的 FLOP:I/O 比例。要注意的是，隨著自回歸的進行，序列長度會逐漸增加，批處理的提升也會逐漸減少。

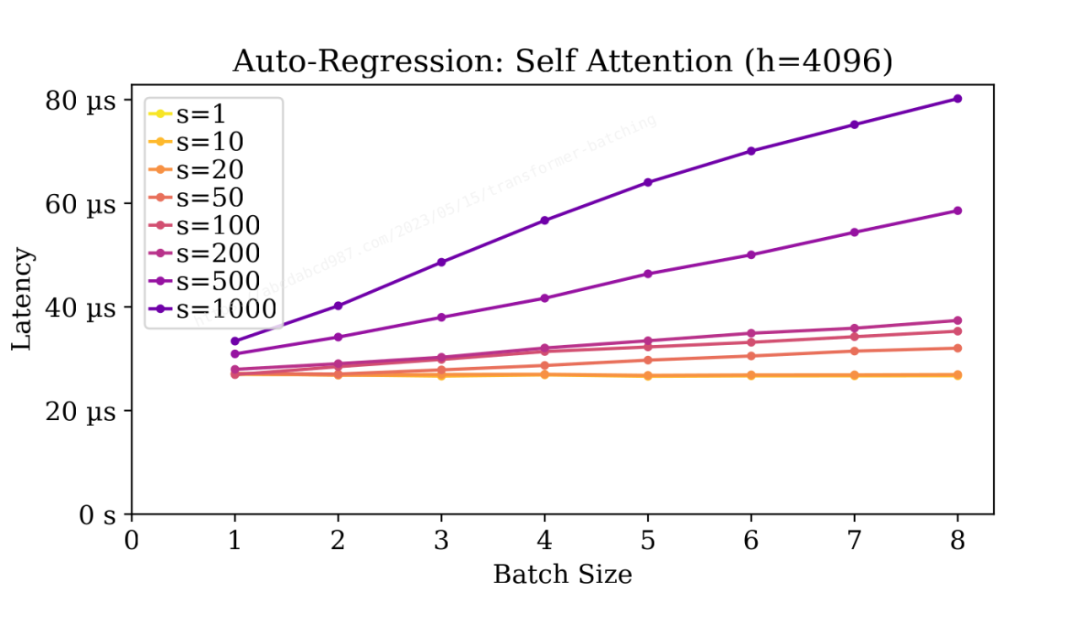
自注意力的延遲與密集層的延遲相當。

與密集層不同，自注意力的延遲隨批大小增加而增加。

延遲與批大小大致呈線性關系。這是因為自注意力本質上是批量矩陣乘法。在固定的 FLOP:I/O 比例下，批處理意味著更多的工作量，但并沒有在單個任務上獲得速度上的提升。

同樣，隨著自回歸的進行，序列長度逐漸增加，每個步驟的處理時間也逐漸增加。

3.4 屋頂模型

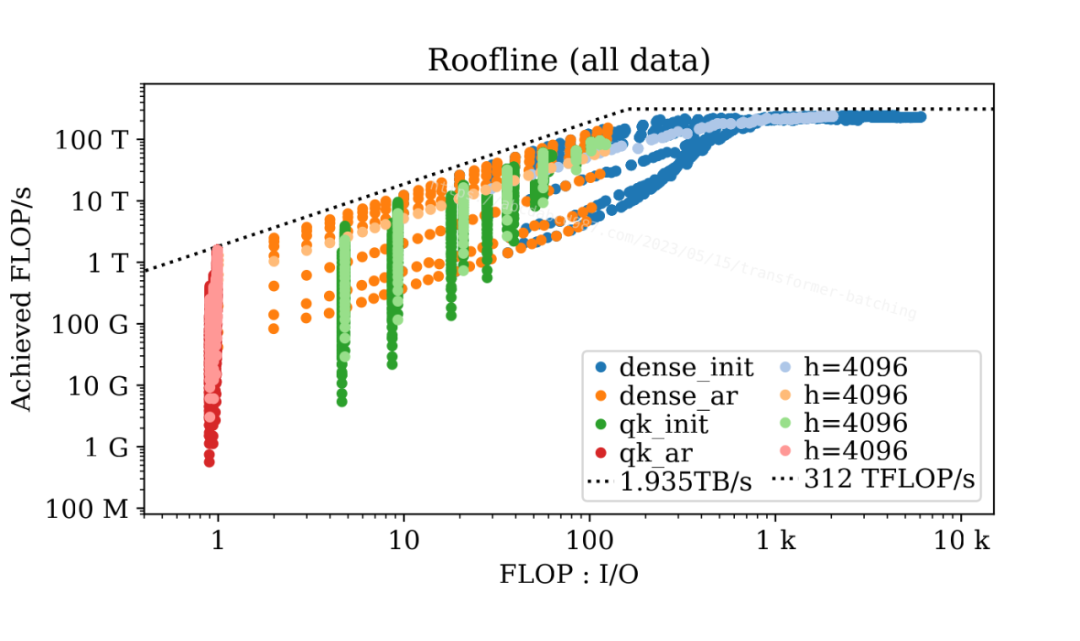
上圖套用屋頂模型 [2]（Roofline Model）展示了基準測試參數的所有組合的數據點。四種顏色代表不同的階段和層。每種顏色都包含一個較淺的版本，展示了 67 億參數模型的數據點作為示例。此外，圖中顯示了來自 NVIDIA A100 參數表 [3]的理論內存帶寬和 FLOP/s。

這張圖有兩個非常有趣的現象。一是數據點聚集成群和子群；二是數據點與理論屋頂線非常接近。

為了探究批處理的影響，讓我們來看一個特定的案例（h=4096, s=100）：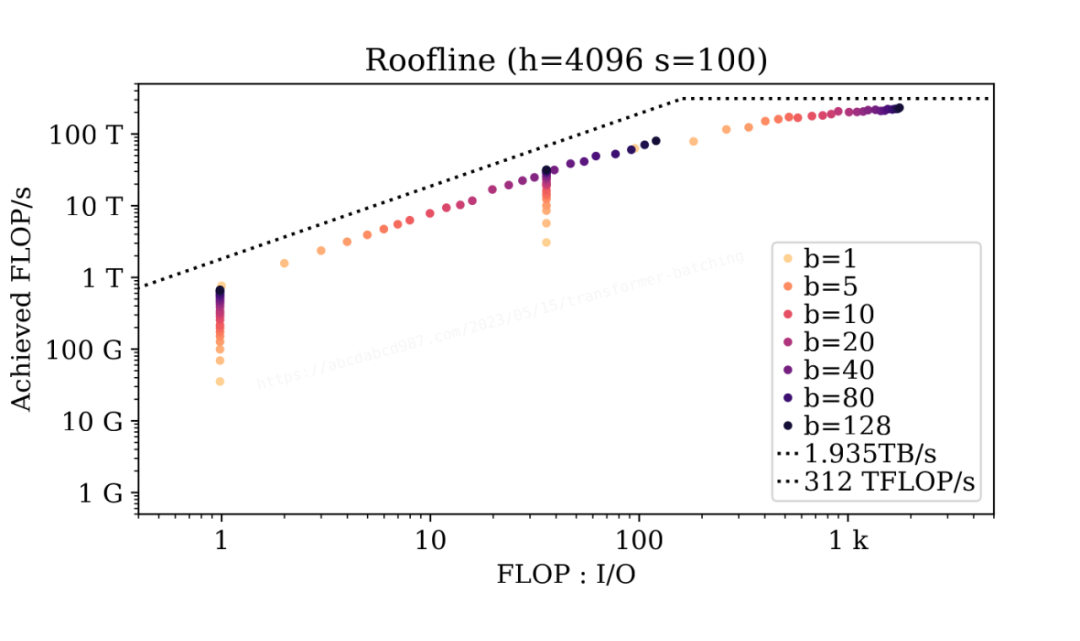

?

從這兩張圖中，我們可以得出以下結論：

算術強度的順序為：dense_init > qk_init > dense_ar > qk_ar。

效率（達成的 FLOP/s）的順序為：dense_init > qk_init > dense_ar > qk_ar。

初始階段的密集層受限于 GPU 的峰值計算性能。當序列長度較短且模型較小時，批處理可以提供輕微的效率提升。其余的情況，要提升初始階段的密集層性能的唯一辦法，就是加錢找老黃買更強的 GPU。

同大小的模型的自回歸階段的密集層數據點形成一條線。這條線的斜率與 GPU 的內存帶寬相同。因此，自回歸階段的密集層受到內存帶寬的限制。增加批大小可以提高密集層的算術強度，于是在內存帶寬約束下增加實現的 FLOP/s。

批處理不會改變自注意力的算術強度。然而，在序列長度較短的情況下，批處理通過并行處理提高了自注意力的達成的 FLOP/s。在不改變算術強度的情況下達成的 FLOP/s 卻增加了，這意味著自注意力的內核實現可能不夠優化，沒有充分利用所有計算單元。

文本生成端到端基準測試

在前面的部分，我們對密集層和自注意力進行了微基準測試。現在，讓我們通過一個端到端的基準測試來研究批處理對文本生成的影響。在這個基準測試中，我使用了 67 億參數的模型，輸入詞元長度為 200，輸出詞元長度為 500。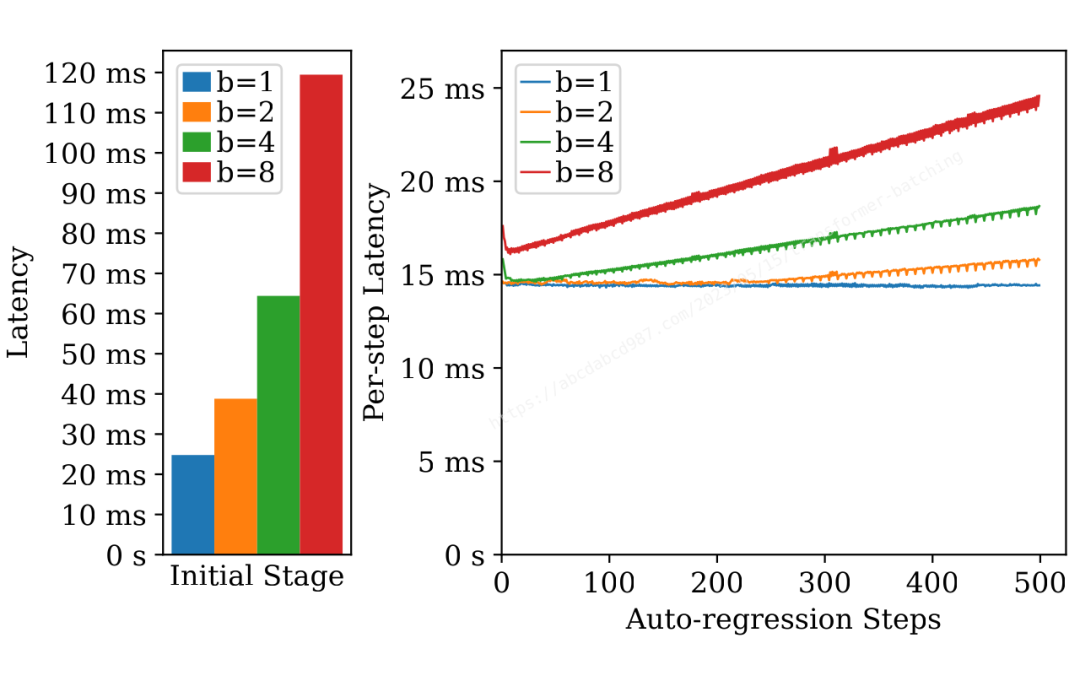

?

上面的圖表顯示了不同批處理大小下初始階段和每個自回歸步驟的延遲。從這個圖表中可以看出一些有趣的現象：

自回歸步驟的延遲與初始階段的延遲相當。考慮到生成數百個新詞元，總延遲主要受自回歸的影響。

初始階段具有輕微的批處理效應，批處理大小為 1 時延遲為 24 毫秒，批處理大小為 8 時延遲為 119 毫秒。

自回歸步驟顯示出明顯的批處理效應。最后一個詞元（即最慢的詞元）在批處理大小為 1 時需要 14 毫秒，在批處理大小為 8 時需要 24 毫秒。

根據這些觀察結果，我們可以做出合理的推測：批處理可以顯著提高吞吐量，而僅對延遲產生輕微影響。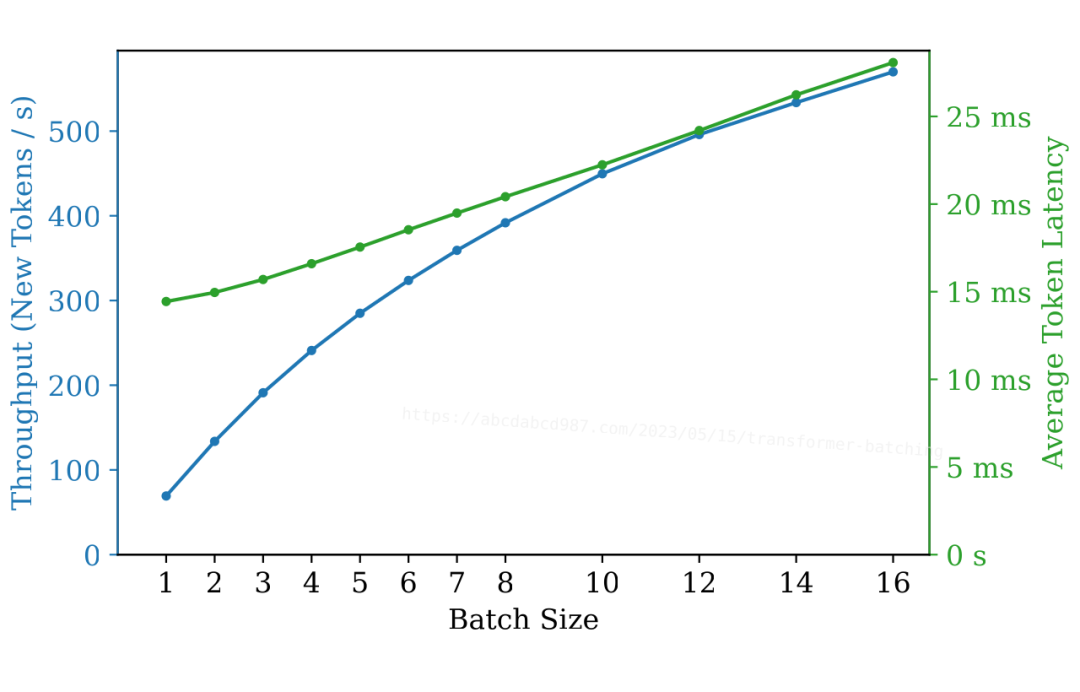

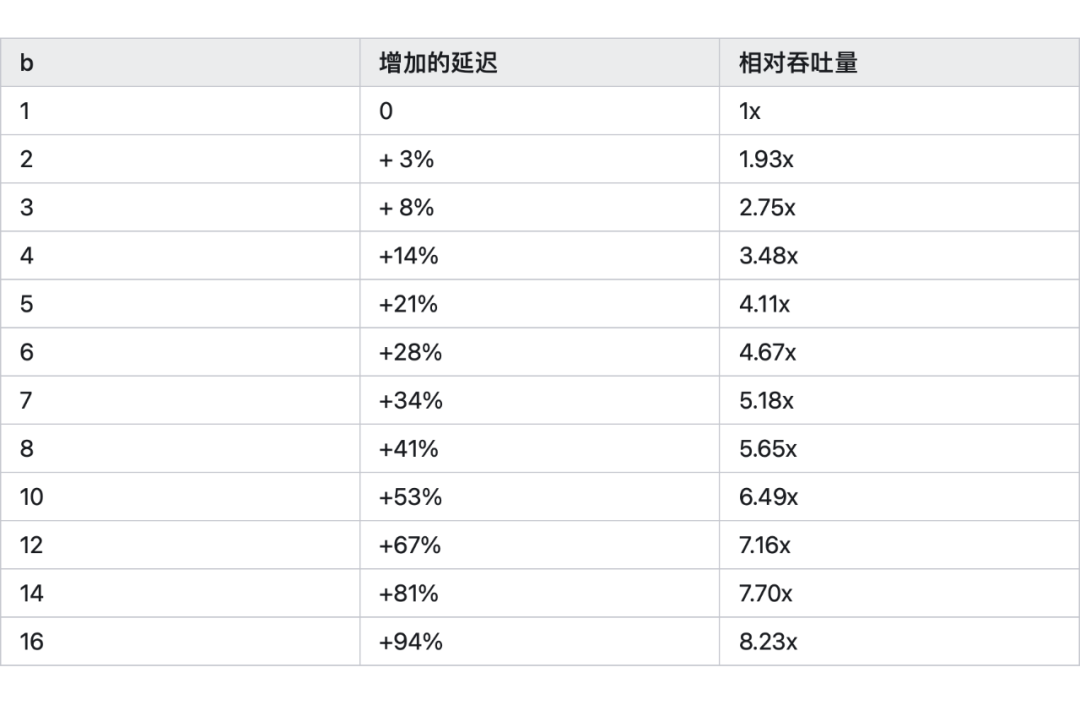
上面的圖表確認了這個推測：

在批處理大小為 2 時，延遲幾乎保持不變，但吞吐量幾乎增加了一倍。

在批處理大小為 4 時，延遲增加了 14%，而吞吐量是原先的 3.5 倍。

延遲與批處理大小大致呈線性關系。

我們可以這樣理解：

圖表中的延遲包含一個初始階段和 500 個自回歸步驟。如前所述，主要影響延遲的是自回歸。因此，我們將重點放在自回歸階段。

回顧微基準測試部分的圖表，我們可以觀察到自注意力的延遲與批處理大小呈線性關系，而密集層的延遲幾乎不受批處理大小的影響。

盡管密集層的運行時間比自注意力長幾倍，但自注意力長仍然對整個層的總延遲產生顯著影響。因此，延遲與批處理大小之間的線性關系延伸到整個層。

此外，隨著批處理大小的增加，吞吐量的提升變少。

我們可以使用一個簡單的分析模型來理解這種邊際收益遞減。

假設批處理大小為 b 的延遲是 c0 + c1 * b，其中 c0 和 c1 是正的常數。

批處理大小為 b 的吞吐量則是 b / (c0 + c1 * b)。

吞吐量的斜率由 c0 / (c0 + c1 * b)^2 給出，它始終為正（表示隨著批處理大小的增加而提高吞吐量），但遞減（意味著邊際收益遞減）。

批處理大小 1 和 2 之間的延遲差異顯著小于較大批次之間的差距。

這是因為批處理大小為 1 時沒有充分利用所有可用的計算單元。因此，當使用批處理大小為 2 運行時，我們可以獲得一些額外的效率而不會產生顯著地增加延遲。

提升大語言模型推斷性能

在研究了大語言模型推斷性能后，讓我們根據我們的發現來做點改進。

5.1 融合自注意力的計算

正如我們之前分析的那樣，QK^T 生成了一個形狀為（b, n, s, s）的臨時輸出，而我們只需要 Softmax(QK^T)V 的最終結果，其形狀為（b, n, s, d）。由于 d=128 相對較小，我們可以將這三個矩陣的乘法融合成一個單獨的 Cuda 核 (Kernel) 函數，直接產生(QK^T)V。

然而，有一個障礙：Softmax。傳統的 Softmax 實現需要讀取 QK^T 的最后一個維度中的所有數字。這會帶來一個問題，因為我們在融合 V 的乘法時只能計算一小塊 QK^T。為了克服這個限制，我們需要找到一種聰明的方式來計算 Softmax，確保它保持結合性。

幸運的是，一些聰明的人已經發現了實現在線 Softmax [4]的方法。我們可以嘗試實現這個技巧并解決一些必要的細節問題。 恭喜你！我們實質上一起重新發明了FlashAttention[NeurIPS'22] [5]論文。此外，我推薦閱讀這篇關于 FlashAttention 的精彩筆記[6]。

5.2 批處理請求

另一個重要的機會在于將請求進行批處理，從而在略微增加延遲的情況下，大幅增加吞吐量，正如我們之前討論的那樣。大語言推斷服務，如OpenAI ChatGPT[7]和HuggingFace Hosted Inference[8]，可以從批處理中獲得極大的好處。

在我們之前的分析中，我們做了一個簡化的假設，即所有請求序列具有相同的長度。然而，在現實中，請求序列的長度是不同的。雖然將所有序列填充到相同的長度是一個選項，但它也會增加計算量。幸運的是，重新審視我們之前的發現，我們可以設計一種更簡單高效的解決方案：

給定形狀為[(s1, h), (s2, h), ...]的輸入，我們將它們堆疊成一個形狀為(sum(si), h)的大矩陣。

對這個堆疊矩陣應用密集層。

將密集層的結果分割回[(s1, h), (s2, h), ...]。

對每個序列進行自注意力計算。

恭喜你！我們實質上一起重新發明了Orca[OSDI'22] [9]論文。

總結

我們將 Transformer 塊的計算步驟、FLOPs、I/O和算術強度濃縮到了一張表格中。

我們考慮了初始階段和自回歸階段，分析了對密集層和自注意力進行批處理的效果。

為了驗證我們的分析，我們進行了微基準測試，并使用屋頂模型解釋了結果。

我們對文本生成進行了端到端基準測試，證明批處理顯著提高了吞吐量，而只增加了微小的延遲。

我們通過融合自注意力的計算，以及支持跨請求批處理，來改進了大語言模型推斷系統。

審核編輯：劉清