很表面很淺薄的問題。

簡單說愛怎么規定就怎么規定，甚至-1到254都行。無非是顯示時通過編碼表做個轉換的問題而已。

不過，當初選擇“補碼”這種編碼形式，卻并不像表面看起來那么淺薄。背后的道道可多著呢。

首先，8位二進制一共可以提供256個“碼點”；那么我們就總可以用這些“碼點”來編碼256種符號。

這種編碼方案有很多。最著名的大概就是ASCII碼方案了，這個方案規定了英文字符（區分大小寫）、0~9這10個數字、標點符號以及一些控制字符如何編碼：

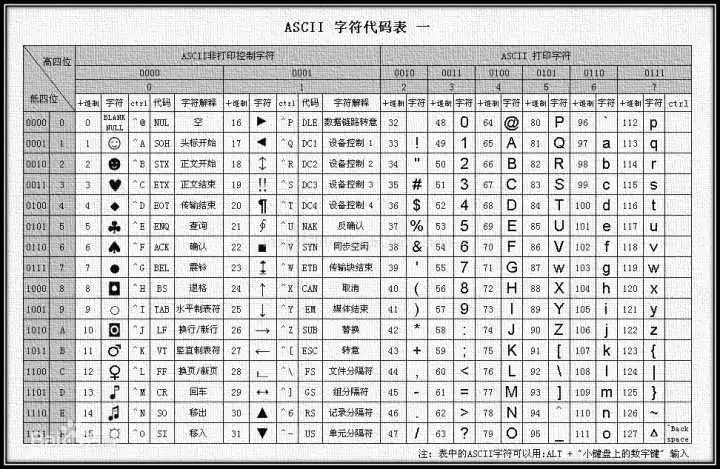
但ASCII碼用來編碼字符效果不錯；拿來存儲數字卻極為浪費。比如它需要三個字節才能表示123。

為了編碼數字，我們需要一個更有效的方案。

一種很自然的想法是，我們就直接把二進制對應的數字值拿來用，這就是最好的編碼方案！

于是，8個二進制位就可以表示0~255之間的所有數字——用ASCII碼三個字節才能表示的123，直接用二進制編碼就是01111011，一個字節足夠了。

這個方案只能表示正數；遇到負數怎么辦呢？

簡單，第一個二進制位拿出來當符號位，剩下七位仍然當數字用，就能表示±127之間的任何數字了。

這個方案就叫“原碼”；其中不帶符號位的就是無符號數（unsigned）。

原碼是一種很初級的編碼方案，它僅僅解決了編碼問題——從此數字有辦法二進制表示了。

但我們在計算機內部表示數字是用來計算的；那么想用原碼計算的話，那可就麻煩了……

我們知道，最初CPU的內部最重要的核心器件叫ALU（Arithmetic and Logic Unit算術邏輯單元），其中的A就是數學。

ALU的核心是加法器，這是個隨參與計算的數值的二進制位數指數增長的數字電路。較早期的CPU里面絕大多數的邏輯門都被拿來做這個加法器了。

加法器顧名思義只能拿來做加法。

但是沒關系，如果你調過機械表，就知道從8點調到1點的方式有兩種：一種是往后撥7個小時，一種是往前撥5個小時。

換句話說，在時鐘鐘面上，8-7和8+(12-7)效果相同，最終得到的都是1.

類似的，1個字節的加減法，如果計算結果超過255就會造成溢出，溢出的高位二進制數據無處存放自動丟棄，計算結果就出錯了——但反過來想，這不恰恰就是一個邏輯鐘面嗎？

顯然，我們也可以利用這個性質做減法：減32完全可以當成加(256-32)來算嘛；而由于二進制的特點，256-32恰好又等于32這個數值取反。

類似的，有符號數其實是一個符號位和7個二進制位，7個二進制位能表示的最大數是127；因此減32就可以用加(128-32)代替（和表盤上的12點/0點一樣）。

于是，減法器就可以不做，一個加法器就足夠用了——省了好大一坨門電路，CPU的制造成本一下子就去了一大塊。

既然最終減法一定要這樣做……那么從一開始就不應該用原碼表示負數，對吧。

不然每次計算都還得用一條指令判斷判斷符號位，然后該取反取反……這速度可就慢下去了。

如果從一開始，負數就取反表示，那么負數加法完全無需判斷，拎起來就加——圓滿。

這個編碼方案就是所謂的反碼。

反碼是一個充滿了工程師的惡臭味的優秀方案。

說它優秀，是因為它的確解決問題；說它惡臭，是因為它用起來實在麻煩，需要很多“微妙”的調整才能得到正確結果。

比如，它的符號位相加后，如果產生了進位，就要把進位送回去加到最低位上——你得搞一大張真值表才能確定這個做法的正確性。

嗯……這就是最容易產生沒人看得懂但絕對不能動不然就會出錯的神奇代碼的重災區——反正它就是能工作；剛開始我還知道為什么得這樣做，一段時間后就只有上帝知道了。

反碼行為奇特的根本原因在于，它有兩個零：＋0和－0，分別對應于00000000和10000000——還記得嗎？我們規定第一位是符號位。因此最前面的0/1是±號，并不是數值。

但＋0和－0都是0.它們是同一個數據，卻得到了兩個碼點。

打個比方的話，這就好像夜里12點就是0點一樣；結果我們的鐘匠師傅沒想明白，偏偏要在鐘面上、12點和1點之間添加一個零點——然而邏輯上我們仍然需要12小時是一圈。

現在，你還想好好調表嗎？算的準準的，8點前擰5個小時就是1點了；結果擰完一看，0點？

徹底亂套了，對吧。

而反碼的計算規則呢，無異于規定了過12點的方向——正著過正常去1點，反著過會先停在-0點上，所以必須推一把。

注意這個調整是計算過程的一部分，每次計算都必須即時調整。這是一個額外的負擔——和顯示時查表轉換到光學點陣/向量是不想干的兩個過程。

或者說，數據的內部表示和外部顯示之間的轉換是另外一個必不可少的流程。這里只要不是太過復雜就不能算額外負擔；而原碼/反碼這兩個編碼方案已經影響了計算過程，造成了額外的性能消耗。

一言以蔽之：能解決問題，但是太難看、太復雜。

一個更好的方案叫補碼。

但是在介紹補碼之前，我先來講一個數學概念—群。

群大概來源于“算術運算以及適用算法運算的集合”的抽象，但又超脫于簡單的四則運算，是一切計算/變換類似行為的總綱。

在群的觀念里，加減乘除都是一種“二元運算”；二元運算是一個集合G中任意兩個元素向群中另一個元素的映射。比如1+1就映射到了2。

注意群有“封閉性”，意思是群中任意兩個元素經過二元運算后，映射的那個元素都還要在群中。因此(自然數,加減法)就不是一個群，因為減法會映射到負數。

此外，二元運算需要滿足結合律，要有單位元（任何元素與之執行二元運算后都會映射到該元素自身），等等。

更復雜的東西我也還看不懂（對不起，俺數學水平太弱雞了）；但了解這么多其實也已經夠了：反碼存在兩個0，意味著對于加法運算來說，它存在兩個不同的單位元；而根據群的定義，群里面有且只有一個單位元。

因此，在反碼這個基礎上無法定義一個群——用人話說就是，你不可能期望找到一種不需要判斷的算法，從而基于反碼模擬加減法運算。

沒錯，反碼有兩個零這事并不像外行想象的那樣無關痛癢——它并不僅僅是浪費了一個碼點的問題，而是破壞了相關結構的性質的問題。

如何解決這個問題呢？

不妨返璞歸真，看看這個問題的本質。

很簡單，和上面等待寫入時間信息的無字鐘面一樣：這里有256個不同的二進制編碼，我們需要給它們分別指定一個意義。

我們希望它們是連續的編碼，且基于二進制的排序不能打亂——這樣我們才能使得基于這些碼點的、拋棄溢出位的加減法運算構成一個群。

只有它們是一個群，我們才能簡單明了的在加法器上支持加減法運算——而不是先算一個瑕疵值然后想辦法彌補、把硬件/軟件變得復雜。

打個比方的話，就是把這些二進制編碼按順序排于鐘面，我們要在上面填上帶±號的數字。

原碼的問題在于，它的編碼排列“不按固定順序”，使得因此必須把負數先“顛倒”一下（實際上取反）才能用；而反碼頭疼醫頭腳疼醫腳，大致保證了編碼順序，卻沒能消除額外的無效碼點，造成在±0這個位置兩個碼點對應一個編碼。

這兩個編碼都沒法自然構造出加法群。

借用@任衛同學的這張圖：

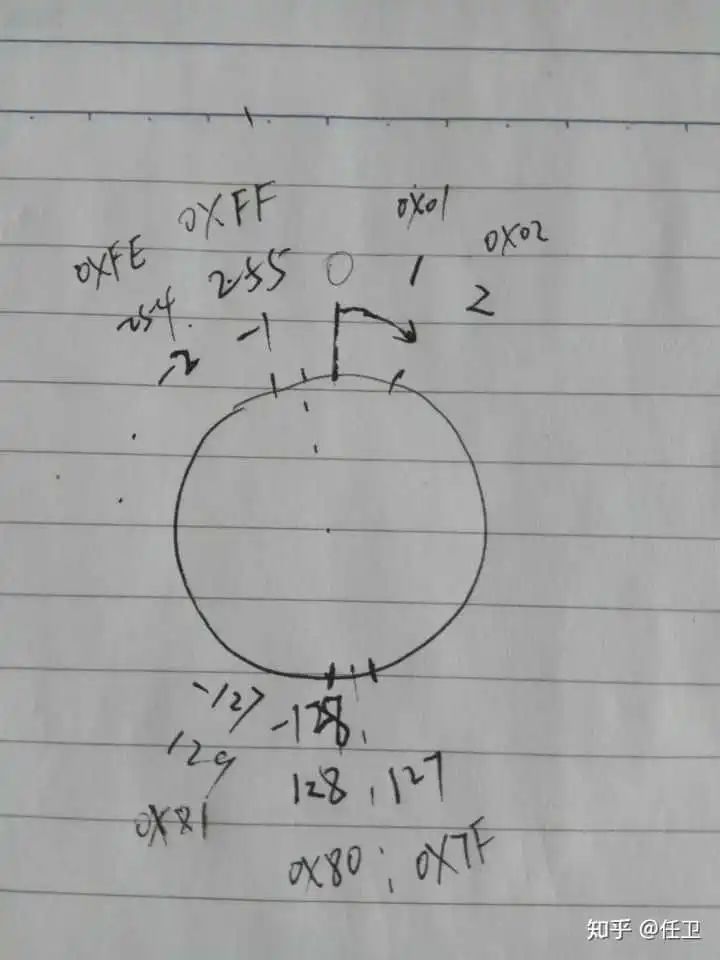
可以很清晰的看出補碼編碼的連續性。

（相比之下，原碼是0 1 2 3……127 -0 -1 -2……-127，順序上一會兒從小到大一會兒從大到小；補碼按照一定的順序編碼但是多了個-0；

只有補碼，嚴格按照統一的順序連續排列數字）。

既然連續，那么通過加一個值（可能為負）調整對稱中心（比如0的位置是00000000還是11111111）、然后再引入模運算剔除高位溢出，這個群就建立起來了。

換句話說，隨便你如何編碼，只要別改變底層的二進制順序、不要有跳躍/重復碼點，那么這個計算就仍然是一個群。

這個計算過程和最終的顯示是完全脫鉤的，你不需要在計算時做任何調整——溢出就隨它溢出，反正（在模運算的層面上）算出來的值總是對的。這是群的性質所保證的。

（注意是“模運算的層面上”，換句話說算出來的實際意義是什么還是得你自己解釋；尤其是產生溢出之后。）

比如，哪怕你把它的編碼范圍改成[-129, 126]或者[-1, 254]，這也僅僅是一個加/減一個整數的映射操作而已；核心計算法則仍然會滿足你的需求）。

甚至，你規定0代表1、1代表0，最終也不過是顯示時換一個不同的譯碼表而已，并不改變問題性質。

這個性質是普適的。

7位、8位或者32位、128位二進制全都適用。

一旦明白了這個……再寫環形緩沖時，你還要費勁巴拉的檢查什么時候需要繞回嗎？求個余（或許還需要再視情況不同增減一個常數），完事。

你看，數學這種東西厲害吧？

哪怕群論門檻都摸不到的這么一點點皮毛知識，帶來的就是眼界水平的差異。

一旦了解了這點皮毛，關于補碼的種種清規戒律神奇規則，也就平常。

但沒有這個眼界，就容易像反碼那樣動輒得咎；反之，隨你怎么玩都不會出界。

沒錯。別看這東西簡單；

但想要做第一個提出的人，你還是需要強悍的洞察力的。

站在群論的肩膀上、反向碾壓這個問題，這是伽羅瓦之后的現代人特有的福利。

審核編輯：黃飛