之前我們在說明數字濾波器的時候，多為Python來進行示例驗證的。實際應用中，多為C/C++，無論是在嵌入式系統中，還是PC機上，尤其對于時間或者實時性要求比較嚴格的情況下，C/C++應該是我們的首選。

本文通過一個帶通濾波器的Python驗證，再轉換到C++代碼模擬驗證的實現過程說明數字濾波器是如何工作的。 我們先通過Python測試驗證，并生成濾波器的參數數據。然后將獲取的參數用到C程序中重現濾波器。 先看圖，后查代碼。在測試中，我們生成了一個混有50Hz，110Hz和210Hz的模擬信號，然后通過濾波器保留50Hz的信號。

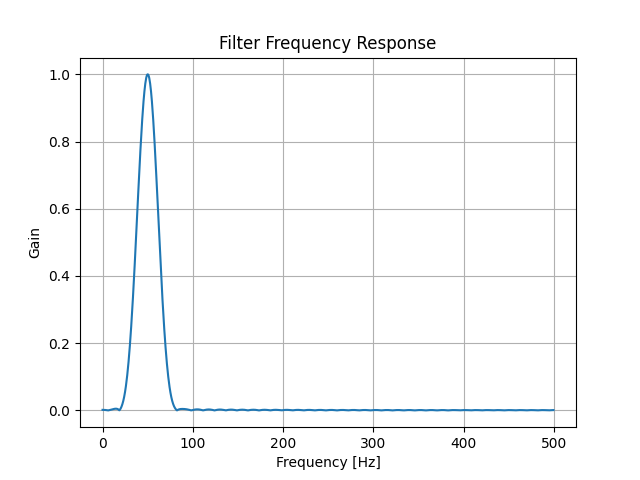
圖-1 濾波器的幅頻響應(50Hz窄帶帶通)

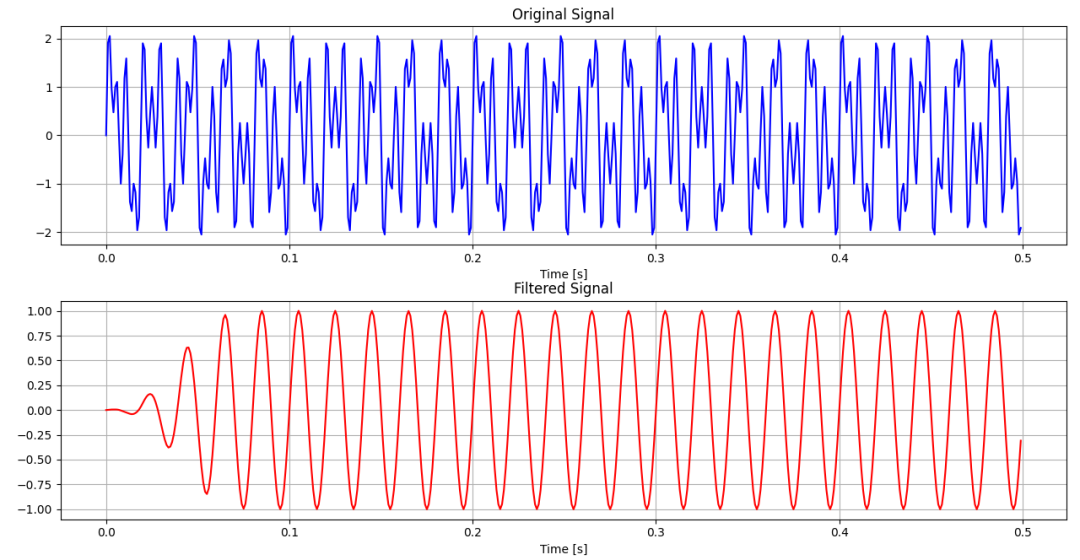
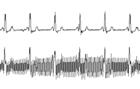
圖-2 模擬信號的濾波前后

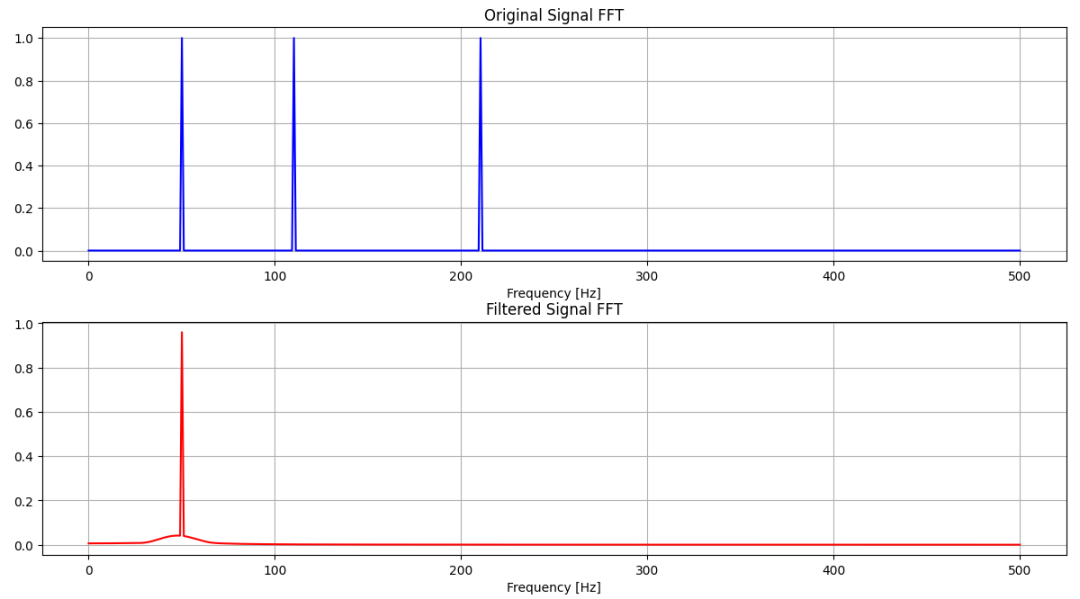
圖-3 模擬信號濾波前后的頻譜圖

相關python代碼：

import numpy as np
from scipy.signal import firwin, freqz, lfilter
import matplotlib.pyplot as plt


fs = 1000.0 # Sample frequency (Hz)
f0 = 50.0 # Frequency to be removed from signal (Hz)
Q = 30.0 # Quality factor
w0 = f0/(fs/2) # Normalized Frequency


# Design band-pass filter
b = firwin(81, [w0 - 0.02, w0 + 0.02], pass_zero=False, window='hamming')
#Outputcoefficients,wegotthecoefficients from this step
b_string = ', '.join(str(coef) for i, coef in enumerate(b))
print('{', b_string, '}')


# Generate frequency response
w, h = freqz(b, [1], worN=1024)


# Convert to Hz
freq = w * fs / (2 * np.pi)


# Plot filter response
plt.plot(freq, abs(h))
plt.title('Filter Frequency Response')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Gain')
plt.grid(True)
plt.show()


# Create a test signal
t = np.arange(0, 1.0, 1/fs) # Time vector
signal=np.sin(2*np.pi*210*t)+np.sin(2*np.pi*50*t)+np.sin(2*np.pi*110*t)#Testsignal


# Apply filter to the test signal
filtered_signal = lfilter(b, [1], signal)


# Original signal & filtered signal
plt.figure(figsize=(12, 8))
plt.subplot(211)
plt.plot(t[:500], signal[:500], color='blue')
plt.title('Original Signal')
plt.xlabel('Time [s]')
plt.grid()


plt.subplot(212)
plt.plot(t[:500], filtered_signal[:500], color='red')
plt.title('Filtered Signal')
plt.xlabel('Time [s]')
plt.tight_layout()
plt.grid()
plt.show()


# Compute and plot the frequency spectrum of signals
N = len(signal)
T = 1/fs
xf = np.linspace(0.0, 1.0/(2.0*T), N//2) # Frequency vector


# Compute FFT of original and filtered signals
fft_signal = np.fft.fft(signal)
fft_filtered = np.fft.fft(filtered_signal)


# Plot FFT of original signal
plt.figure(figsize=(12, 8))
plt.subplot(211)
plt.plot(xf, 2.0/N * np.abs(fft_signal[0:N//2]), color='blue')
plt.title('Original Signal FFT')
plt.xlabel('Frequency [Hz]')
plt.grid()


# Plot FFT of filtered signal
plt.subplot(212)
plt.plot(xf, 2.0/N * np.abs(fft_filtered[0:N//2]), color='red')
plt.title('Filtered Signal FFT')
plt.xlabel('Frequency [Hz]')
plt.grid()
plt.tight_layout()


plt.show()

濾波器通過C++語言的功能復現和驗證。

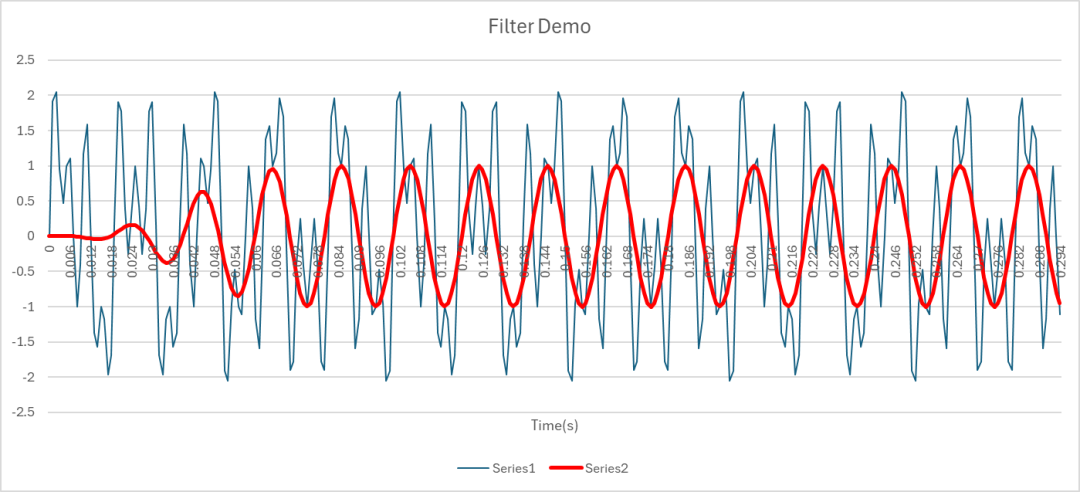
圖-4 模擬信號經C++濾波器的前后波形(取部分，請對照圖-2)

這里的測試過程中，模擬信號由代碼直接生成，然后經濾波器處理后，將該模擬信號和經濾波之后的信號數據全部存到csv文件中。在csv文件中，我們可以再現數據濾波前后的變化。 以下為濾波器的C++代碼，大家可以再優化。直接上代碼。

#include 
#include 
#include 
#include 
#include 


#define SAMPLE_RATE 1000.0


using namespace std; // 聲明使用std命名空間


const double pi = 3.14159265358979323846;


// 模擬信號函數
vector generateSignal(int sampleRate, int seconds)
{
  vectorsignal(sampleRate * seconds);   //定義模擬信號的數組長度
  for (unsigned int i = 0; i < (unsigned int)(sampleRate * seconds); ++i)
  {
????//?包含50Hz，110Hz和210Hz信號
    signal[i] = sin((2 * pi * i * 50) / sampleRate) + sin((2 * pi * i * 210) / sampleRate) + sin((2 * pi * i * 110) / sampleRate);
  }
  return signal;
}


// 濾波器函數
vectorfilter(constvector&b,constvector&a,constvector&signal)
{
  vector output(signal.size());
  for (size_t i = 0; i < signal.size(); ++i)
  {
    for (size_t j = 0; j < b.size(); ++j)
    {
      if (i >= j)
      {
        output[i] += b[j] * signal[i - j];
      }
    }
    for (size_t j = 1; j < a.size(); ++j)
    {
      if (i >= j)
      {
        output[i] -= a[j] * output[i - j];
      }
    }
    output[i] /= a[0];
  }
  return output;
}


// 寫入文件函數
void writeToFile(const vector& signal, const vector& filtered_signal, const string &filename)
{
  ofstream file(filename);


  for (std::size_t i = 0; i < signal.size(); i++)
  {
    file << i/SAMPLE_RATE << ", " << signal[i] <<", "<< filtered_signal[i]<< "
";
??}
}
// 主函數
int main()
{
  // 系數
  vector b{0.0010175493084400998, 0.0010954624020866333, 0.001080635650435545, 0.0009293052645812359,
                   0.0005868808563577278, -8.138309855847798e-19, -0.0008644147524968251, -0.0019966389877814107,
                   -0.003323586744207458, -0.004696461345361978, -0.005892320462621699, -0.006633249964255378, 
                   -0.006623614506478284, -0.005601944833604465, -0.0034001773970723163, -7.334366341273803e-18, 
                   0.004425290874832446, 0.00949426225087417, 0.014634010415364655, 0.019132982942933127, 
                   0.022226796444847933, 0.023207550009729024, 0.021541722692400025, 0.01697833945185371, 
                   0.009628503914736117, -6.755395515820625e-18, -0.01102370844120733, -0.02226281209657117, 
                   -0.032372473621654914, -0.04001099412924139, -0.04402269970024527, -0.043609484958132556, 
                   -0.03846490807520255, -0.028848803480728435, -0.015588116829396594, -9.10410551538968e-18, 
                   0.016255406162706088, 0.031374390998733945, 0.04363491329762711, 0.051616779739690075, 
                   0.05438594145724075, 0.051616779739690075, 0.04363491329762711, 0.031374390998733945, 
                   0.016255406162706088, -9.10410551538968e-18, -0.015588116829396594, -0.028848803480728435, 
                   -0.03846490807520255, -0.043609484958132556, -0.04402269970024527, -0.0400109941292414, 
                   -0.032372473621654914, -0.022262812096571168, -0.01102370844120733, -6.755395515820627e-18, 
                   0.009628503914736117, 0.016978339451853702, 0.021541722692400025, 0.023207550009729034, 
                   0.022226796444847933, 0.01913298294293312, 0.014634010415364655, 0.009494262250874175, 
                   0.004425290874832446, -7.3343663412738e-18, -0.0034001773970723163, -0.005601944833604469, 
                   -0.006623614506478284, -0.006633249964255374, -0.005892320462621699, -0.00469646134536198, 
                   -0.003323586744207458, -0.001996638987781409, -0.0008644147524968251, -8.138309855847805e-19, 
                   0.0005868808563577278, 0.0009293052645812359, 0.001080635650435545, 0.0010954624020866333, 
                   0.0010175493084400998};
  vector a{1};


  // 生成模擬信號
  vector signal = generateSignal(1000, 1); // 1秒的模擬信號


  // 濾波處理
  vector output = filter(b, a, signal);


  // 寫入至csv文件
  writeToFile(signal, output, "output.csv");


  return 0;
}