BP神經網絡(Backpropagation Neural Network)是一種多層前饋神經網絡,具有強大的非線性映射能力,廣泛應用于模式識別、信號處理、預測等領域。本文將詳細介紹BP神經網絡的算法過程,包括網絡結構、激活函數、訓練過程、反向傳播算法、權重更新策略等。
- 網絡結構
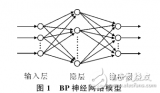
BP神經網絡由輸入層、隱藏層和輸出層組成,每層包含若干神經元。輸入層的神經元數量與問題的特征維度相同,輸出層的神經元數量與問題的輸出維度相同。隱藏層的數量和每層的神經元數量可以根據問題的復雜度和數據量進行調整。
1.1 輸入層
輸入層是BP神經網絡的第一層,負責接收外部輸入信號。輸入層的神經元數量與問題的特征維度相同,每個神經元接收一個輸入信號。
1.2 隱藏層
隱藏層是BP神經網絡的中間層,負責對輸入信號進行非線性變換和特征提取。隱藏層的數量可以根據問題的復雜度進行調整,通常設置1到3層。每層隱藏層的神經元數量可以根據數據量和問題規模進行調整。
1.3 輸出層
輸出層是BP神經網絡的最后一層,負責生成預測結果。輸出層的神經元數量與問題的輸出維度相同,每個神經元生成一個預測值。
- 激活函數
激活函數是BP神經網絡中神經元的非線性變換函數,用于引入非線性特性,提高網絡的表達能力。常用的激活函數包括Sigmoid函數、Tanh函數、ReLU函數等。
2.1 Sigmoid函數
Sigmoid函數是一種常用的激活函數,其數學表達式為:
f(x) = 1 / (1 + exp(-x))
Sigmoid函數的輸出范圍在(0, 1)之間,具有平滑、連續的特點,適用于二分類問題。
2.2 Tanh函數
Tanh函數是Sigmoid函數的變體,其數學表達式為:
f(x) = (exp(x) - exp(-x)) / (exp(x) + exp(-x))
Tanh函數的輸出范圍在(-1, 1)之間,相對于Sigmoid函數,Tanh函數在x=0附近的變化更加陡峭,適用于多分類問題。
2.3 ReLU函數
ReLU(Rectified Linear Unit)函數是一種非線性激活函數,其數學表達式為:
f(x) = max(0, x)
ReLU函數在x>0時輸出x,x<0時輸出0。ReLU函數具有計算簡單、收斂速度快的特點,廣泛應用于深度學習中。
- 訓練過程
BP神經網絡的訓練過程包括前向傳播和反向傳播兩個階段。
3.1 前向傳播
前向傳播是BP神經網絡從輸入層到輸出層的信號傳遞過程。在前向傳播過程中,輸入信號經過每層神經元的加權求和和激活函數變換,最終生成預測結果。
具體步驟如下:
- 初始化輸入層神經元的輸入值。
- 對于每一層神經元,計算加權求和:net = w * x + b,其中w為權重矩陣,x為輸入向量,b為偏置項。
- 對加權求和的結果應用激活函數,得到該層神經元的輸出值。
- 將當前層的輸出值作為下一層的輸入值,重復步驟2-3,直到輸出層。
3.2 反向傳播
反向傳播是BP神經網絡從輸出層到輸入層的誤差傳遞過程。在反向傳播過程中,根據預測結果和真實值計算誤差,并通過梯度下降算法更新網絡權重。
具體步驟如下:
- 計算輸出層的誤差:E = (y - t),其中y為預測結果,t為真實值。
- 對輸出層的誤差應用激活函數的導數,得到輸出層的梯度:dE = E * f'(net),其中f'(net)為激活函數的導數。
- 對于每一層神經元,從后向前計算梯度和誤差:
a. 計算當前層的誤差:delta = dE * w^T,其中w^T為上一層權重矩陣的轉置。
b. 計算當前層的梯度:dW = x * delta,其中x為當前層的輸入向量。 - 更新網絡權重:W = W - alpha * dW,其中alpha為學習率。
-
信號處理
+關注
關注
48文章
1042瀏覽量
103401 -
BP神經網絡
+關注
關注
2文章
115瀏覽量
30603 -
非線性
+關注
關注
1文章
213瀏覽量
23131 -
神經元
+關注
關注
1文章
363瀏覽量
18511
發布評論請先 登錄
相關推薦




 bp神經網絡算法過程包括
bp神經網絡算法過程包括











評論