讀書期間對于深度學習也有涉及,不過只是皮毛,在這個數據和算法的時代,也需要更加貼近算法。于是從一名工程師角度出發,希望通過幾篇文章,將深度學習基礎記錄下來,同時也是對于自己學習的總結和積累。
神經網絡概述
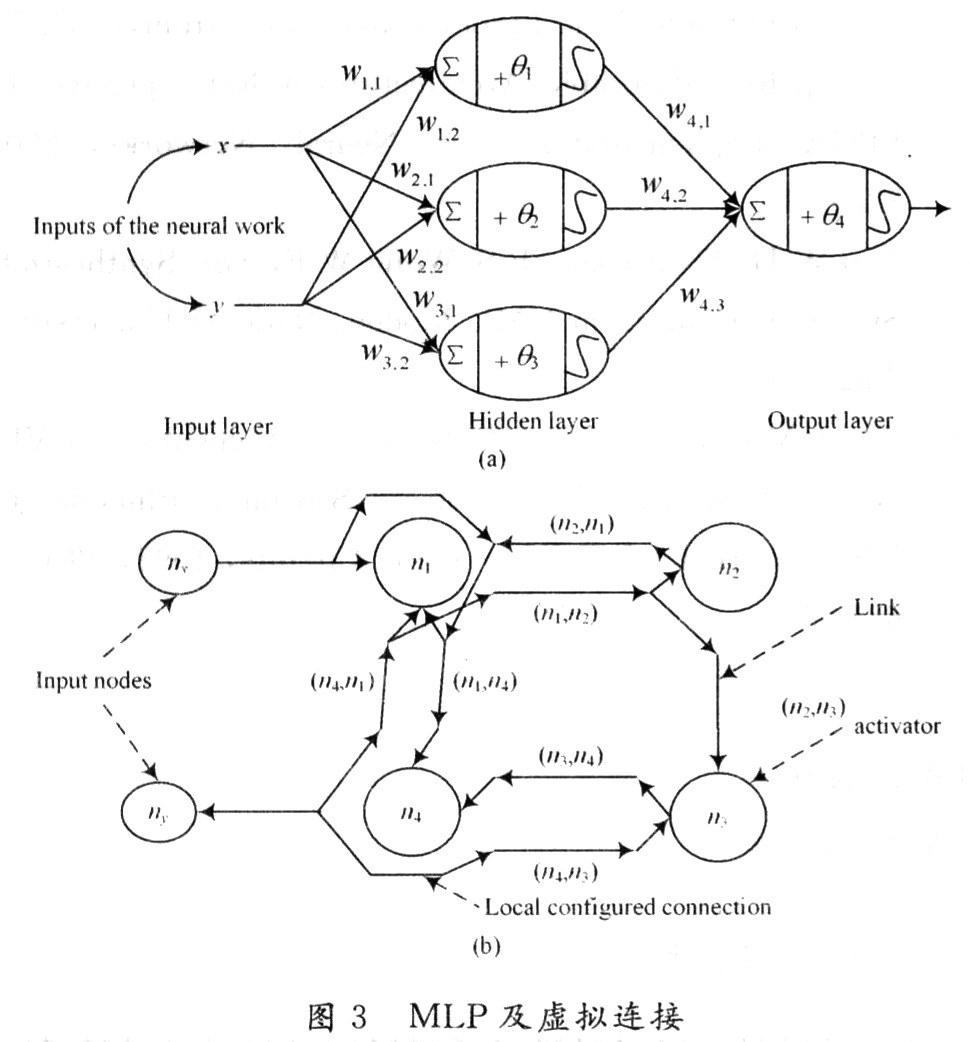
這是一張典型的人工神經網絡的圖,圖中的節點稱為神經元,圖共分為三層,第一層為輸入層,第二層為隱藏層,第三層為輸出層。輸入層接受外部世界的輸入,具像化為圖像的像素值,實體的特征值等,輸出層概率預測結果,具像化為該圖像是人像,該實體為潛在商家。
神經元一個神經元將多個輸入及其權值統一為下層節點的一個輸入。例如:
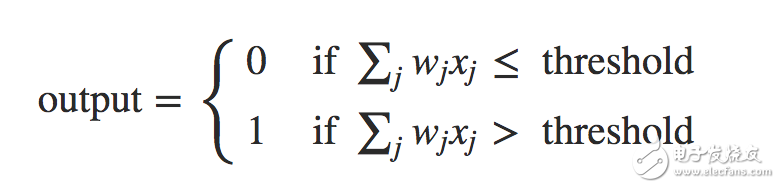
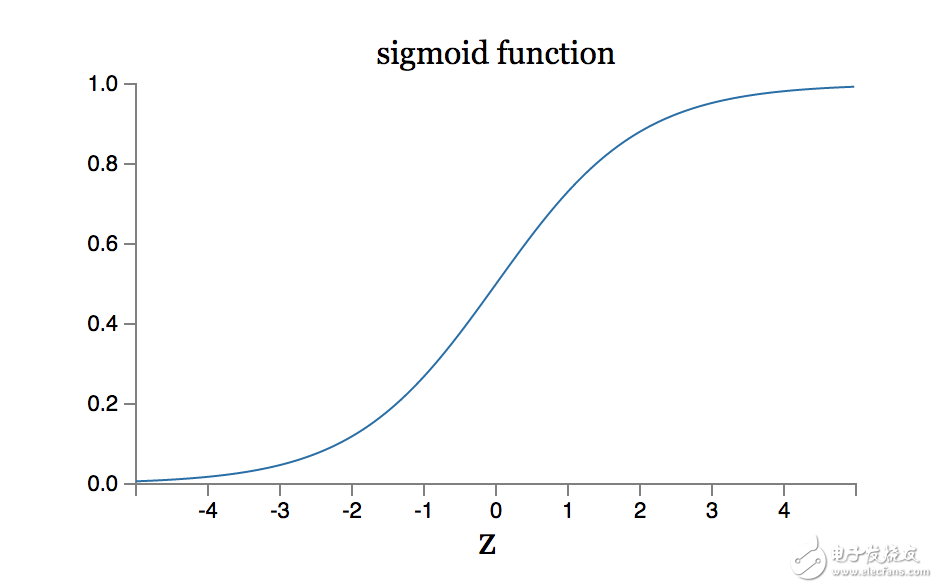
而神經元一般都使用sigmoid函數,至于為什么使用sigmoid函數,也是個很有探討意義的問題,具體可以看這篇文章了解sigmoid的特性。
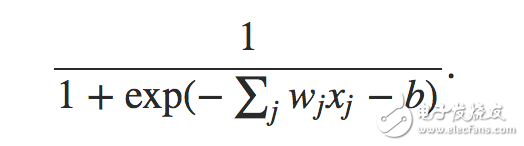
其中,w表示權重向量,x表示輸入向量,b為該節點的閾值。
那么下面問題就是如何選擇合適的權重和閾值,構建出來合適的網絡。
構建合適的網絡
網絡結構往往決定了算法復雜度和模型可調度,輸出層主要由向量決定,輸出層主要由預測類型決定,主要問題就在中間層數和節點數的選擇上,節點數和層數越多意味著模型可調節性越強,預測結果的粒度越細,但同時也意味著計算復雜度越高。經驗中間層一般選1-2層,節點數作為可調參數。
選擇合適權重和閾值
首先,定義損失函數,損失函數的意義在于對于訓練集評價預測結果和真實結果之間的差異
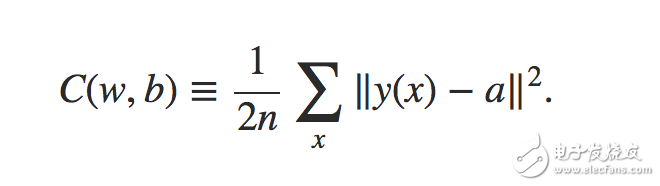
該損失函數其實是預測結果與真實結果之間的方差
我們希望通過調整權重w和閾值b的值來使預測結果和真實結果之間的差更小。相當于在一個解空間中尋找最優解。解法有很多,如梯度下降法,擬牛頓法等。
梯度下降法
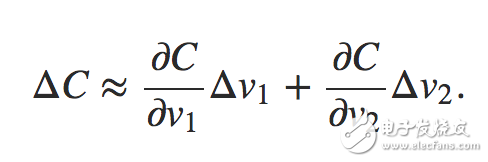
通過上述公式可以看出,對于損失函數的變化可以描述為損失在每個維度v上的變化值之和,用向量表示為
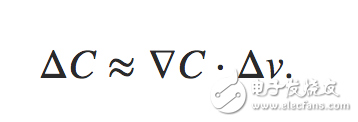
為了是損失更小而不是更大,損失的變化應該小于0,于是取
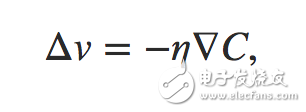
則,損失的下降可以表示為反向傳播
反向傳播其實是對于當一次預測結束后,評估每個參數對于預測結果誤差的貢獻,并對其進行調整,調整方法可以通過損失函數對于權值的求導得到:
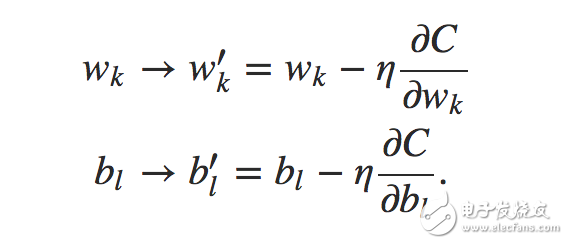
通過多次迭代,獲得損失函數的極小值。步長決定了函數的收斂速度。
小結下:
人工神經網絡就好像一個在陌生的城市迷路的孩子,每走一步都對該步進行評估,計算其到達目的地的可能性,并逐漸走到目的地。人工神經網絡比較重要的有三部分:
1. 結構:層級網絡
2. 求解方法:梯度下降
3. 求解思想:反向傳播
-
神經網絡
+關注
關注
42文章
4781瀏覽量
101178 -
ANN
+關注
關注
0文章
23瀏覽量
9215
發布評論請先 登錄
相關推薦
人工神經網絡算法的學習方法與應用實例(pdf彩版)
【PYNQ-Z2試用體驗】神經網絡基礎知識
卷積神經網絡如何使用
【案例分享】ART神經網絡與SOM神經網絡
人工神經網絡實現方法有哪些?
如何構建神經網絡?
基于FPGA的人工神經網絡實現方法的研究
人工神經網絡基礎描述詳解
卷積神經網絡CNN架構分析-LeNet
神經網絡的復習資料免費下載
人工神經網絡和bp神經網絡的區別
ANN神經網絡——器件建模





 一文詳解神經網絡基礎ANN
一文詳解神經網絡基礎ANN










評論