在傳統的開關電源中，通常采用磁性元件實現濾波，能量儲存和傳輸。開關器件的工作頻率越高，磁性元件的尺寸就可以越小，電源裝置的小型化、輕量化和低成本化就越容易實現。但是，開關頻率提高會相應的提升開關器件的開關損耗，因此軟開關技術應運而生。

要實現理想的軟開關，最好的情況是使開關在電壓和電流同時為零時關斷和開通(ZVS，ZCS)，這樣損耗才會真正為零。要實現這個目標，必須采用諧振技術。

【LLC眾籌】最全張飛60小時半橋LLC諧振電源教程，活動最后6天！>立即參與眾籌<

二、LLC串聯諧振電路

根據電路原理，電感電容串聯或并聯可以構成諧振電路，使得在電源為直流電源時，電路中得電流按照正弦規律變化。由于電流或電壓按正弦規律變化，存在過零點，如果此時開關器件開通或關斷，產生的損耗就為零。下邊就分析目前所使用的LLC諧振半橋電路。基本電路如下圖所示：

其中Cr，Lr，Lm構成諧振腔（Resonant tank），即所謂的LLC，Cr起隔直電容的作用，同時平衡變壓器磁通，防止飽和。

2.1 LLC電路特征

（1）變頻控制

（2）固定占空比50％

（3）在開關管輪替導通之間存在死區時間（Dead Time），因此Mosfet可以零電壓開通（ZVS）,二次側Diode可以零點流關斷，因此二極管恢復損耗很小

（4）高效率，可以達到92％+

（5）較小的輸出漣波，較好的EMI

2.2 方波的傅立葉展開

對于圖2.1的半橋控制電路，Q1,Q2在一個周期內交替導通，即占空比為50％。所以VA為方波，幅值等于Vin，其傅立葉級數展開為

其基波分量為

其中fsw為開關頻率，V_o.FHA（t）為諧振腔輸入方波電壓的基波分量。

相應地，諧振腔輸出電壓（即理想變壓器輸出）也為方波

其基波分量為

其中Ψ為輸出電壓相對輸入電壓的相移，實際上為零。

2.3 FHA 電路模型

將圖2.1所示電路的非線性電路做等效變換，可以得到下圖：

FHA（First harmonic approximation）：一次諧波近似原理。該原理是假設能量的傳輸只與諧振回路中電壓和電流傅立葉表達式中的基波分量有關，因此，如果忽略開關頻率的影響，則諧振腔被正弦輸入電流Irt激勵，其表達式為：

其中為輸入電流相對輸入電壓的相移。

相應地，諧振腔輸出電流i_rect為

由于V_o.FHA（t）與i_rect（t）同相位，所以諧振電路的輸出阻抗為

其中Rout為負載阻抗，該阻抗折算到變壓器原邊的反射阻抗Rac為

所以，諧振腔的輸入阻抗Zin（s）為

變壓器增益傳遞函數H(S)為

電壓增益M(fsw)為

2.4 電壓增益M（fn，λ，Q)分析

對電壓增益M（fsw）表達式中的變量進行替換，得到關于fn，λ，Q三個參量的函數，新的表達式為

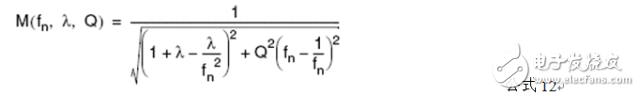
式中參數定義如下：

諧振頻率

特征阻抗

品質因數

Lr與Lm電感值比

歸一化頻率

作出λ=0.2時M（fn，λ，Q)曲線簇如下圖：

（橫軸為fn，縱軸為M）

其中紅色曲線為空載時（Q=0）的電壓增益曲線MOL，隨著fn趨向于無窮，MOL逐漸趨向于M∞。

從圖中可以看到，對于不同的Q值曲線，都會經過Load－independent point（fr，unity gain），且該點所有曲線的切線斜率-2λ。很幸運，load－independent point出現在電壓增益特征曲線的感性區域，這里諧振腔電流滯后于輸入電壓方波（這個是ZVS的必要條件）。

通過改變輸入諧振回路的方波電壓頻率可以穩定轉換器的輸出電壓：由于工作區域為電壓增益特性的感性部分，所以，當輸出功率減小或者輸入電壓增加時，通過提高工作頻率來穩定輸出電壓。考慮到這個問題，如果轉換器工作點與load-independent point很接近，那么輸出電壓的穩定將會與寬負載變化相逆，相應地開關頻率變化范圍也會很小。

明顯地，輸入電壓范圍越寬，則工作頻率范圍也會相應地變的更寬，因此，很難對電路進行優化設計。這也是目前所有的諧振拓撲結構中普遍存在的缺點。

一般來說，大功率場合一般都有一級PFC電路。對于寬電壓輸入（85Vac～264Vac），經過PFC之后都會升壓到400V，且變化范圍不大（10％～15％）。所以對于前端有PFC的LLC電路來講，LLC輸入電壓的波動很小，因此上述問題不是很嚴重。

工作電壓變化范圍是：最小工作電壓由PFC pre-regulator 持續能力決定（hold－up capability）during mains dips；最大工作電壓由OVP線路的門限值決定。因此，當輸入電壓在正常值時，諧振轉換器可以在load-independent point優化設計，而最小輸入電壓during mains dips交給諧振腔自身的提升能力處理。（比如工作點低于諧振點）

另外，還可以得到一個空載時（二次側Diode不導通）的諧振頻率fo

2.4.1 Mmin和fmax的選取

當輸入電壓Vdc最大，輸出負載最小時，電壓最小增益Mmin須大于M∞

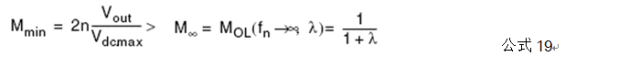
此時最大歸一化頻率為

2.4.1 Mmax和fmin的選取

當輸入電壓Vdc最小，輸出負載最大時，電壓最小增益Mmax

此時最小歸一化頻率為

關于λ的分析，λ增加相應的變化為：

（1）M-fn平面上的增益曲線向著諧振頻率fnr收縮，這同時意味著空載諧振頻率fno增加；

（2）空載增益特性漸近線M∞逐漸減小；

（3）每一條增益曲線的最大增益增加。

2.4 歸一化阻抗Zn（fn，λ，Q)分析

作出λ=0.2時Zn（fn，λ，Q)曲線簇如下圖：

（橫軸為fn，縱軸為Zn）

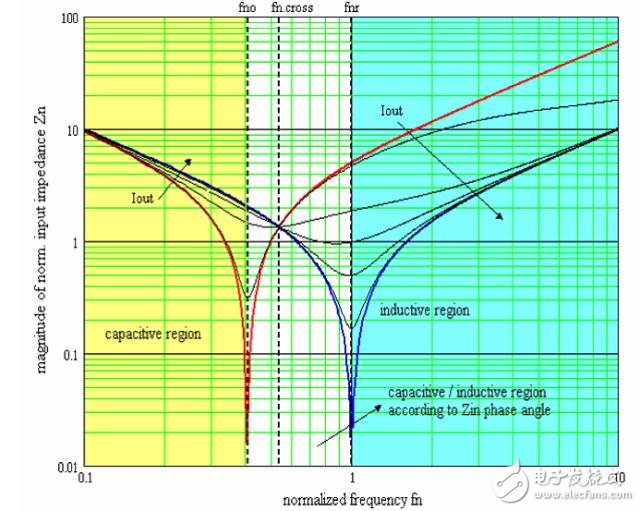
其中，紅色和藍色曲線分別為空載和短路時的歸一化阻抗特性曲線，所有的Zn以兩個歸一化諧振頻率fno和fnr為漸近線，且不同Q值的曲線相交于一點，該點的歸一化頻率fn.cross：

當工作頻率大于交叉頻率fcross時，輸入阻抗隨輸出電流的增大而減小，當工作頻率小于交叉頻率時，輸入阻抗隨輸出電流的增大而增大。輸出阻抗一直減小。

根據fn可以將整個圖分為三個區間

fn

fn>fnr 感性工作區

fno

題外話，通過阻抗特性評估轉換器的效率η

輸入功率

輸出功率

所以效率η

其中Y_in.LOSS為輸入阻抗的導納（admittance），等于輸入阻抗的倒數(reciprocal)

假設Zn的虛部為零，即Zin為零相位（特征阻抗Zo為真實值，不影響相位），可以從中解出LLC諧振變換器工作于感性和容性區域的臨界頻率fz，做歸一化處理得到：

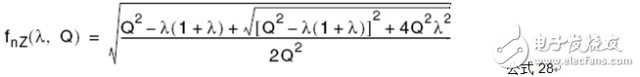
其中fnz只與固定的λ－Q相關，此時輸入諧振腔阻抗只有實部（從電源只吸收有用功）。

同時，可以得到最大品質因數

最大品質因數Qmax：當小于Qmax時，對于相同的fn－λ時，諧振腔阻抗呈感性，因此，最大的電壓增益Mmax

將Qz（fn，λ）帶入M（fn，λ，Q）中，得到如Mz (fn, λ)的表達式

因此，在fnr和fno之間的部分可以畫出Mz (fn，λ)以確定感性和容性的分界線borderline，如下圖，從圖中還可以看到，對于單一Q值曲線來講，最大的增益點總是落在容性區域

3.1 概述

假設工作在感性區域只是半橋MOSFET ZVS的必要條件（necessary condition），并不是充分條件(sufficientcondition)，因為半橋中點的并聯電容（在FHA分析中被忽略）在轉換過程中需要充電（charged）和消耗（depleted）。為了了解ZVS的工作情況，參照下圖

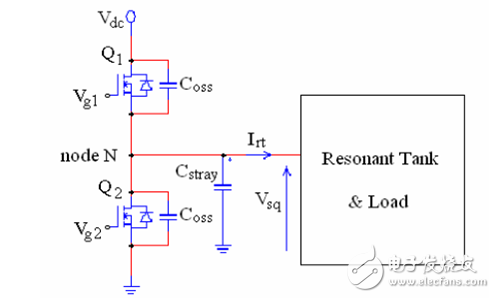
其中存在兩個電容，分別為POWER MOSFET的等效漏源極電容（輸出電容）Coss和諧振腔阻抗雜散（stray）電容Cstray，因此節點N處的總電容Czvs為

轉換過程如下圖

3.2 ZVS充分條件

為了達到ZVS,在兩個MOSFET輪換開通之間存在死區時間TD。由于工作在感性區域，因此輸入電流滯后于輸入電壓，當半周期結束時，諧振腔的電流Irt仍然在流入，這個電流可以消耗儲存在Czvs上的電荷，從而使節點N的電壓降為零，所以在另一個開關開啟時為零電壓開通。

在半周期結束時，諧振電流腔中的電流必須可以保證在TD時間內，將Czvs的電荷消耗完，這就是ZVS的充分條件，臨界電流Izvs為

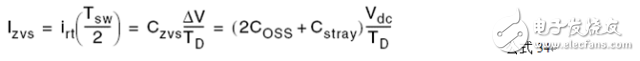
這個電流等于流過諧振腔的無功電流的峰值（90度異相），這個電流決定電路的無功功率

而有功功率的輸入電流Iact

所以輸入電流Irt

諧振腔電流滯后電壓的相位Φ（工作點的輸入阻抗相位）

因此我們可以得到整個工作區間內，半橋POWER MOSFET ZVS的充分條件（sufficient condition）的相位判定

3.3 通過選取Qmax來保證ZVS的實現

滿載條件下的Qzvs1

求tanΦ對于解出品質因數（滿載，最小輸入電壓，最大增益，最小工作頻率）并不方便，因此我們計算Qmax（最大輸出功率，最小輸入電壓），此時輸入阻抗為零相位(由上邊關于Qmax的描述可以看到，Qmax是在Zn虛部為零的條件下得到的，即相位Φ等于0，而零相位則無法滿足ZVS的充分條件，也就是說半周期結束時的Irt不會大于臨界值Izvs)，所以選取（5％-10％）的差度，保證相位Φ不為零：

從上式得到的結果要驗證是否滿足tan 的條件，不滿足則需要重新設計。

空載條件下的Qzvs2

當然，ZVS的充分條件需要滿足空載且最大輸入電壓時的情況，這樣，滿載時ZVS的最大品質因數增加了約束條件Qzvs2。空載時，Q=0，所以

而

由ZVS充分條件知

將上式簡化得到空載且最大輸入電壓時的品質因數

因此，為了確保在整個工作區間，諧振腔可以ZVS，必須滿足最大品質因數Qmax小于min（Qzvs1，Qzvs2）

參考上圖中的電壓增益特性，假設諧振腔被設計以最大輸出功率Pout.max工作于感性區域，相應地，Q=Qmax，并假定輸出電壓相對輸入電壓的增益大于1，如圖中M=Mx

當輸出功率逐漸由零開始向最大值增加，相應的對于不同負載的增益也會逐步地從紅色曲線（Q=0）進入到黑色曲線（Q=Qmax）。控制回路會保持M始終等于Mx不變，因此靜態工作點（quiescent point）會沿著M=Mx的水平線移動，相應地，水平線M=Mx和Q值曲線的交點的橫坐標就是不同負載條件下的工作頻率。

如果負載增加到超過最大規定值Q=Qmax，最后轉換器的工作點一定進入容性區域，此時將會出現MOSFET硬開關，如果沒有矯正措施則可能會導致設備故障。

事實上，如果Q相對Qmax足夠大，與M=Mx的交叉點將會出現在分界線Mz的左半平面，即容性區域；如果Q值曲線的正切線超過M=Mx，工作點將不會沿M=Mx移動。這意味者轉換器將不能保證輸出電壓的穩定，盡管工作頻率會降低（反饋反轉feedback reversal），但是輸出電壓仍會下降。

限制最小工作頻率（M=Mx與Q=Qmax的交點橫坐標）并不能阻止轉換器進入容性工作區域。事實上，當工作頻率到達最小值時，如果負載繼續增加，則會導致工作點沿著垂直線分f＝fmin移動，最后穿過分界線。

限制最小工作頻率只有在最小工作頻率歸一化后大于1才有效果。所以，考慮到輸出端過載和短路的情況，轉換器的工組哦頻率必須大于諧振頻率fr，以降低功率吞吐量（power throughout）。

值得注意的是，如果在一段限制時間內，轉換器規定傳輸峰值輸出功率（輸出電壓穩定必須保持）遠大于最大連續輸出功率，諧振腔必須以峰值輸出功率設計，確保其不會進入容性工作區間。當然，熱設計則可以只考慮最大連續輸出功率即可。

無論如何，不論轉換器被如何規定，短路或者一般的過載情況（超過最大諧振腔規定）都需要附加手段處理，比如限電流電路。

LLC諧振半橋非常適合磁集成，比如說，將電感和變壓器集中到單一磁性設備。這可以很容易從變壓器的物理模型看出，顯然可以看到與LLC電路中的電感部分類似的拓撲結構。然而，理想變壓器在二次側存在漏電感，而在前邊的討論中都被忽略了。為了將二次側漏感的效果考慮進FHA分析中，我們學要一個特殊的變壓器模型和一個簡單化的假設。

眾所周知，由于模型中理想變壓器圈比的選擇很多，因此對于一個給定的變壓器，存在無窮多種電氣等效模型。對一個合適的“等效”圈比n（顯然不同于物理上的圈比nt＝N1：N2），所有與漏磁通相關的元件都可以等效到一次側。

這種等效模型稱作APR(All-Primary-Referred)，即所有參數都等效于一次側，該模型滿足FHA分析。通過選擇n可以得到APR模型：

k ：變壓器耦合系數coupling coefficient

L1：一次側繞組電感值

L2：單邊二次繞組電感值

注意：

（1）Lr仍舊保持了物理模型中的意義：短路二次側繞組時測量得到的一次側電感值

（2）一次側電感L1不可以改變

兩種模型(physical model and APR model)不同的地方只是在分割方式上，因此L1與Lr之間的不同點就是Lm。

最后，倘若這些參數通過等效APR模型闡述得到，以上所作的分析可以直接應用在現實世界中的變壓器。反之亦然（vice versa），基于FHA分析得到的設計流程將提供APR模型的參數；因此，必須增加步驟決定物理模型中的那些參數。

尤其在計算圈比nt（physical model）時，由于Lr與Lm與現實世界中存在聯系 Lr+Lm＝L_L1+Lμ=L1

在物理模型中，問題無法在數學上得到解決：因為含有5個未知量L_L1，Lμ，nt，L_L2a，L_L2b；而APR模型中只有3個參數：Lr，Lm，n.

克服了該問題的假設是建立在磁路對稱（magnetic circuit symmetry）：假設一次側和二次側繞組的漏磁通剛好相等。由此假設可以得到：

3.1 設計規格

輸入電壓范圍：Vdc.Min-Vdc.max

正常輸入電壓：Vdc.nom

輸出電壓：Vout

諧振頻率：fr

最大工作頻率：fmax

啟機頻率：fstart

3.2 附加信息

節點 N 的并聯電容：Czvs

死區時間：TD

3.3 一般設計準則

準則1：轉換器設計工作在正常輸入電壓（nominal input voltage）

準則2：轉換器必須能夠自動調節，當輸入電壓最大且零負載

準則3：轉換器必須在一直工作于ZVS區域

3.4 10個設計步驟

1)由準則1知，設正常輸入電壓下，諧振頻率點的增益等于1，計算變壓器（APR）圈比：

2)分別取輸入電壓范圍的極值，計算最大與最小增益

3)按照定義計算最大歸一化工作頻率

4)計算反射到變壓器一次側的等效負載阻抗

5)計算最大輸入電壓，最大工作頻率，零負載條件下，電感比值λ

6)計算最小輸入電壓，滿載時，工作于ZVS區域的最大Q值（選擇90％～95％）

7)計算最大輸入電壓，空載時，工作于ZVS區域的最大Q值

8)選擇整個工作范圍內(空載～滿載)可允許最大的Q值，即Qzvs

9)計算最小輸入電壓，滿載時，最小工作頻率

10)計算諧振腔特征阻抗和所有的元件值（Lr，Lm，Cr）