正弦量是一個非常重要的概念，它描述了隨時間變化的交流電信號。為了更好地理解和分析正弦量，我們需要掌握其基本要素等相關知識。下面將詳細介紹這些內容。

一、正弦量的基本要素

正弦量具有三個基本要素，分別用于描述其大小、變化快慢和初始狀態。

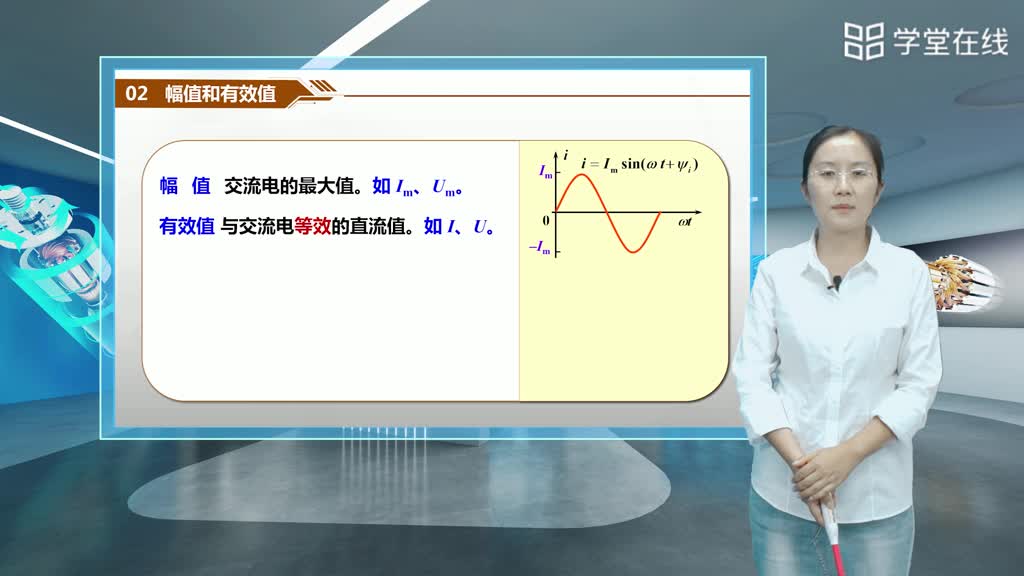
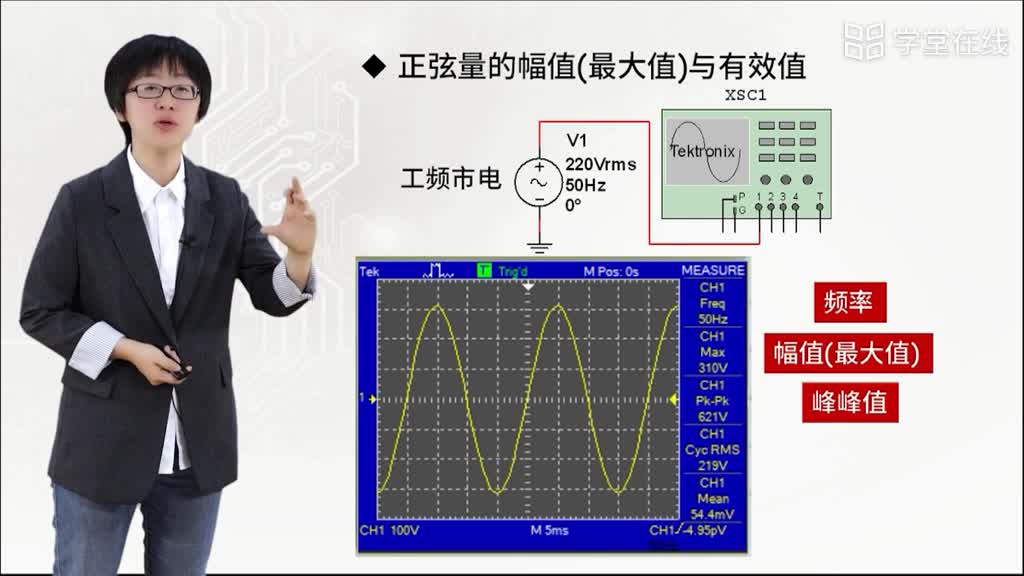
表示大小的量：有效值和最大值。有效值是指正弦量在一個周期內的均方根值，而最大值則是指正弦量在一個周期內所達到的最大值。這兩個量共同決定了正弦量的大小。

表示變化快慢的量：周期T、頻率f和角頻率。周期T是指正弦量完成一個完整周期所需的時間；頻率f是單位時間內正弦量重復的次數；角頻率則是與正弦量的相位變化率相關的量。這三個量共同描述了正弦量的變化速度。

表示初始狀態的量：相位、初相位和相位差。

二、復數的基本知識

復數是實數的擴展，可以用于表示有向線段。復數A的模r表示有向線段的長度，而輻角則表示有向線段與x軸正方向之間的夾角。復數有多種表示方式，包括代數式、三角式、指數式和極坐標式等。其中，代數式用于復數的加減法運算，指數式或極坐標式用于復數的乘除法運算。

三、正弦量的相量表示法

相量是一種用復數來表示正弦量的方法。相量的模表示正弦量的大小，而輻角則表示正弦量的初相位。為了與一般的復數相區別，相量的符號上通常會加一個小圓點。

最大值相量是用復數的模來表示正弦量的最大值。有效值相量則是用復數的模來表示正弦量的有效值。需要注意的是，由于正弦量有三個要素（大小、變化快慢和初始狀態），而復數只有兩個要素（模和輻角），因此在相量中只表示出了正弦量的大小和初相位，沒有表示出交流電的周期或頻率。這意味著相量并不等同于正弦量本身。

用相量表示正弦量后，我們可以將正弦量的加減、乘除、積分和微分運算都變換為復數的代數運算。這使得正弦量的計算變得更加簡單和直觀。此外，相量的加減法也可以用作圖法實現，方法與復數運算的平行四邊形法和三角形法相同。