StackOverflow人氣答主(top 0.12%)Amro通過一個簡單的二元分類決策樹例子,簡明扼要地解釋了信息熵和信息增益這兩個概念。
為了解釋熵這個概念,讓我們想象一個分類男女名字的監督學習任務。給定一個名字列表,每個名字標記為m(男)或f(女),我們想要學習一個擬合數據的模型,該模型可以用來預測未見的新名字的性別。
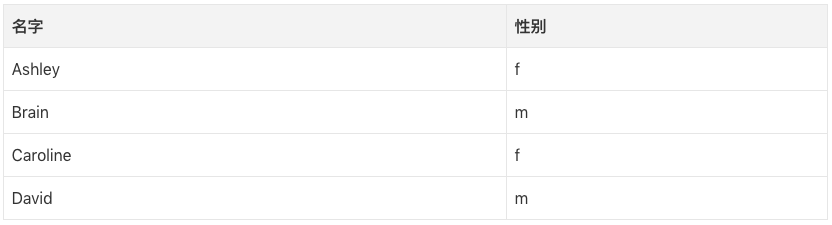
現在我們想要預測“Amro”的性別(Amro是我的名字)。
第一步,我們需要判定哪些數據特征和我們想要預測的目標分類相關。一些特征的例子包括:首/末字母、長度、元音數量、是否以元音結尾,等等。所以,提取特征之后,我們的數據是這樣的:
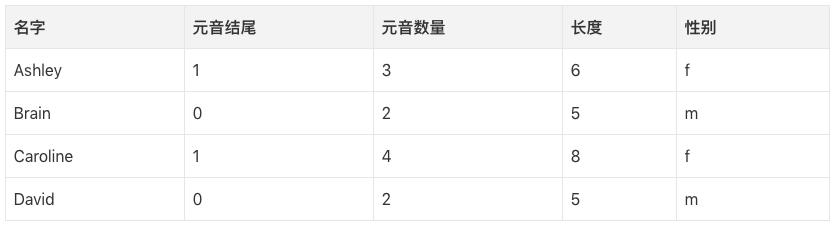
我們可以構建一棵決策樹,一棵樹的例子:
長度<7
| 元音數量<3: 男
| 元音數量>=3
| | 元音結尾=1: 女
| | 元音結尾=0: 男
長度>=7
| 長度=5: 男
基本上,每個節點代表在單一屬性上進行的測試,我們根據測試的結果決定向左還是向右。我們持續沿著樹走,直到我們到達包含分類預測的葉節點(m或f)。
因此,如果我們運行這棵決策樹判定Amro,我們首次測試“長度<7?”答案為是,因此我們沿著分支往下,下一個測試是“元音數量<3?”答案同樣為真。這將我們導向標簽為m的葉節點,因此預測是男性(我碰巧是男性,因此這棵決策樹的預測正確)。
決策樹以自頂向下的方式創建,但問題在于如何選擇分割每個節點的屬性?答案是找到能將目標分類分割為盡可能純粹的子節點的特征(即:只包含單一分類的純粹節點優于同時包含男名和女名的混合節點)。
這一純粹性的量度稱為信息。它表示,給定到達節點的樣本,指定一個新實例(名字)應該被分類為男性或女性的期望的信息量。我們根據節點處的男名分類和女名分類的數量計算它。
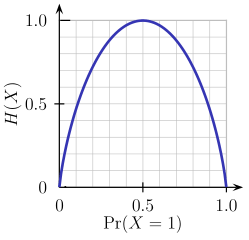
另一方面,熵是不純粹性的量度(與信息相反)。對二元分類而言,熵的定義為:
Entropy = - p(a)*log(p(a)) - p(b)*log(p(b))
這一二元熵函數的圖像如下圖所示。當概率為p=1/2時,該函數達到其最大值,這意味著p(X=a)=0.5或類似的p(X=b)=0.5,即50%對50%的概率為a或b(不確定性最大)。當概率為p=1或p=0時(完全確定),熵函數達到其最小值零(p(X=a)=1或p(X=a)=0,后者意味著p(X=b)=1)。
當然,熵的定義可以推廣到有N個離散值(超過2)的隨機變量X:
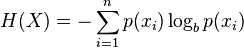
(公式中的log通常為以2為底的對數)
回到我們的名字分類任務中,讓我們看一個例子。想象一下,在構建決策樹的過程中的某一點,我們考慮如下分割:
以元音結尾
[9m,5f]
/ \
=1 =0
------- -------
[3m,4f] [6m,1f]
如你所見,在分割前,我們有9個男名、5個女名,即P(m)=9/14,P(f)=5/14。根據熵的定義,分割前的熵為:
Entropy_before = - (5/14)*log2(5/14) - (9/14)*log2(9/14) = 0.9403
接下來我們將其與分割后的熵比較。在以元音結尾為真=1的左分支中,我們有:
Entropy_left = - (3/7)*log2(3/7) - (4/7)*log2(4/7) = 0.9852
而在以元音結尾為假=0的右分支中,我們有:
Entropy_right = - (6/7)*log2(6/7) - (1/7)*log2(1/7) = 0.5917
我們以每個分支上的實例數量作為權重因子(7個實例向左,7個實例向右),得出分割后的最終權重:
Entropy_after = 7/14*Entropy_left + 7/14*Entropy_right = 0.7885
現在比較分割前后的權重,我們得到信息增益的這一量度,也就是說,基于特定特征進行分割后,我們獲得了多少信息:
Information_Gain = Entropy_before - Entropy_after = 0.1518
你可以如此解釋以上運算:通過以“元音結尾”特征進行分割,我們得以降低子樹預測輸出的不確定性,降幅為一個較小的數值0.1518(單位為比特,比特為信息單位)。
在樹的每一個節點,為每個特征進行這一運算,以貪婪的方式選擇可以取得最大信息增益的特征進行分割(從而偏好產生較低不確定性/熵的純分割)。從根節點向下遞歸應用此過程,停止于包含的節點均屬同一分類的葉節點(不用再進一步分割了)。
注意,我省略了超出本文范圍的一些細節,包含如何處理數值特征、缺失特征、過擬合、剪枝樹,等等。
-
決策樹
+關注
關注
3文章
96瀏覽量
13587 -
信息熵
+關注
關注
0文章
13瀏覽量
7119
原文標題:信息論視角下的決策樹算法:信息熵和信息增益
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
關于決策樹,這些知識點不可錯過
決策樹C4.5算法屬性取值優化研究
決策樹的原理和決策樹構建的準備工作,機器學習決策樹的原理
如何使用最優二叉決策樹分類模型進行奶牛運動行為的識別
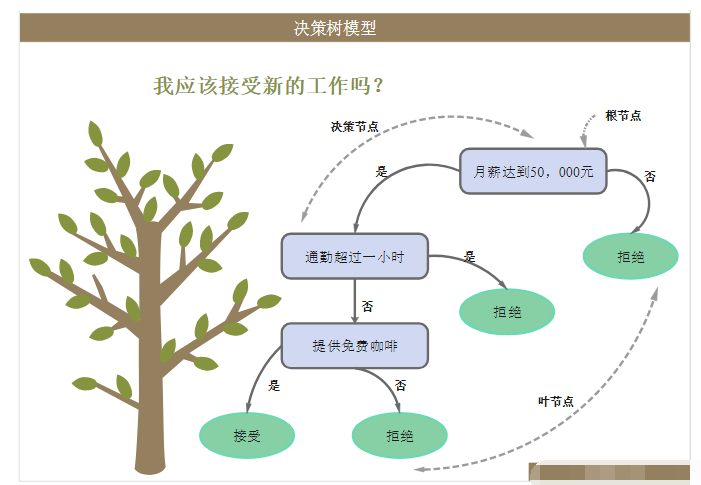
什么是決策樹模型,決策樹模型的繪制方法




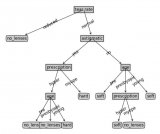
 Amro通過一個簡單的二元分類決策樹解釋信息熵和信息增益這兩個概念
Amro通過一個簡單的二元分類決策樹解釋信息熵和信息增益這兩個概念
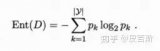










評論