五 向量運算的啟示

計算簡單, 幾何意義明確——模相乘, 相位相加.
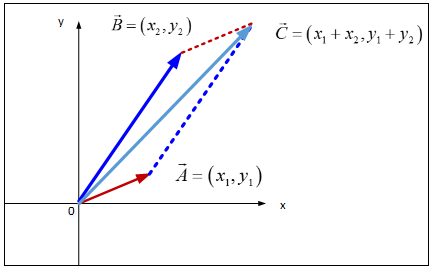
圖14 向量加的直角坐標表示
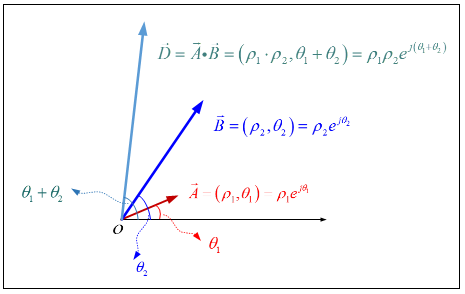
圖15 向量乘法的極坐標表示
向量運算的例子告訴我們, 選擇不同的坐標系, 不僅影響運算的復雜度, 在解釋運算的幾何意義時也各有千秋. 上例告訴我們, 如果是向量的加法, 直角坐標系比極坐標系方便; 如果是向量的乘法, 很顯然, 極坐標系比直角坐標系方便.
回到數字信號處理的話題, 卷積和是讓無數人困惑的公式, 然而, 它又是經典數字信號處理算法的根源. 既然卷積和運算就是濾波, 我們如何評判濾波的效果呢? 從什么角度理解系統的濾波行為更好呢?
再想想知了的叫聲, 之所以煩人, 是因為包含了大量的高頻分量. 看來, 用頻率這一參數來解釋信號特性很符合人的直觀感覺. 我們有更好的方式來洞悉卷積和的物理意義嗎? 能不能站在頻(率)域的角度來解釋卷積和呢? 當然可以, 因為我們有卷積定理(性質):
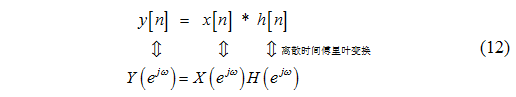
通過傅里葉變換, 將時域中的卷積和運算換成了頻域中的相乘運算. 那么頻域中的相乘運算有什么好處呢? 不要忘了, 我們主要是為了直觀解釋濾波的行為和特性.


在上述的討論中, 我們只關注幅度譜, 實際中, 相位譜也必須考慮, 更完整的表達式為

通過向量乘法運算的例子, 我們可以看到, 向量的表示方式起到了關鍵性的作用; 同樣地, 信號也有不同的描述方式, 如時域、頻域、復頻域, 不同的表示方法都是為了使分析問題更簡單、物理意義更明確.
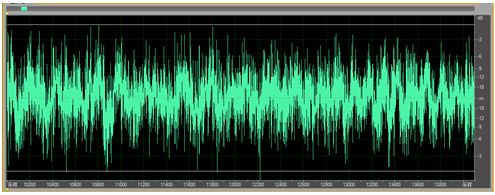
圖16 濾波前知了聲x[n]時域波形
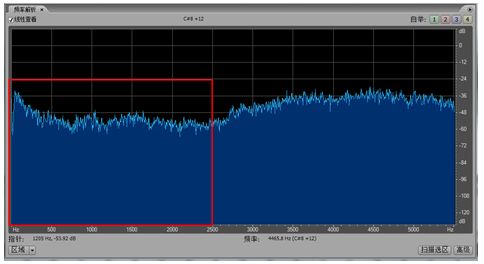

(紅框是希望保留的低頻分量)
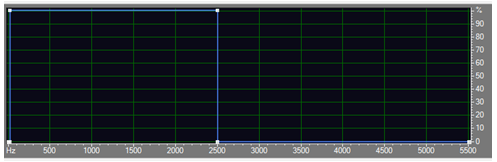

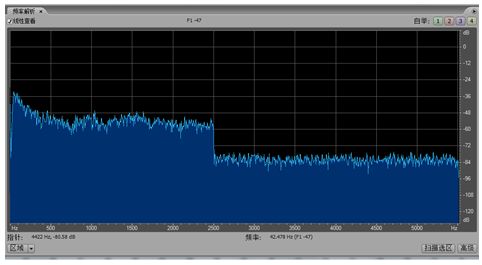

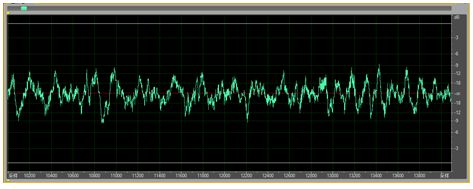

六 濾波器設計征程
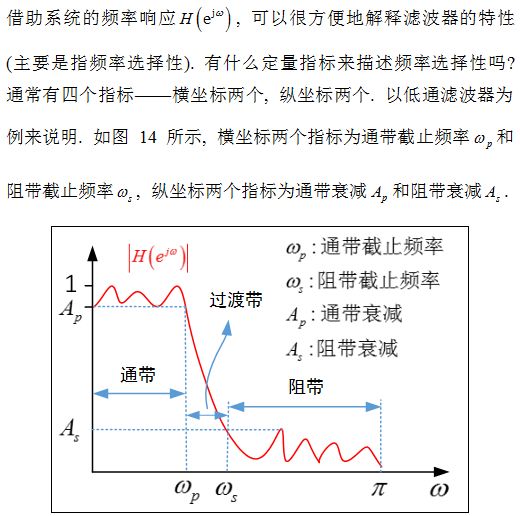
圖21 數字低通濾波器指標






clc;
closeall
fs = 11025; %采樣頻率(Hz)
Fp =2000; %通帶截止頻率(Hz)
Fs =2500; %阻帶截止頻率(Hz)
Ap =0.1; %通帶衰減(dB)
As =50; %阻帶衰減(dB)
wp = 2*Fp/fs; %歸一化通帶截止頻率
ws = 2*Fs/fs; %歸一化阻帶截止頻率
[N,Wp]= ellipord(wp, ws, Ap, As); %確定帶通濾波器的階數和截止頻率
[b, a]= ellip(N, Ap, As, Wp); %確定濾波器系數
[h, w]= freqz(b, a); %求數字帶通濾波器的頻率響應
%以下為繪圖命令, 繪制帶通濾波器的幅頻響應
figure;
plot(w*fs/(2*pi),20*log10(abs(h)/max(abs(h))));
axis([0,fs/2, -100,0]);
title('數字低通濾波器的幅度響應');
xlabel('頻率(Hz)');
ylabel('幅度(dB)');
grid
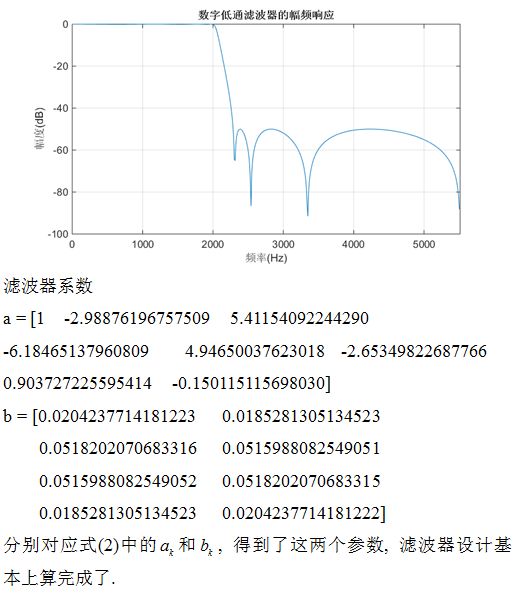
如果你掌握了濾波器設計的基本理論, 但又不想寫代碼, 你可以利用FDATool輕松完成濾波器設計的全過程.
在命令窗口輸入: fdatool, 回車, 就可以看到下圖所示的界面:
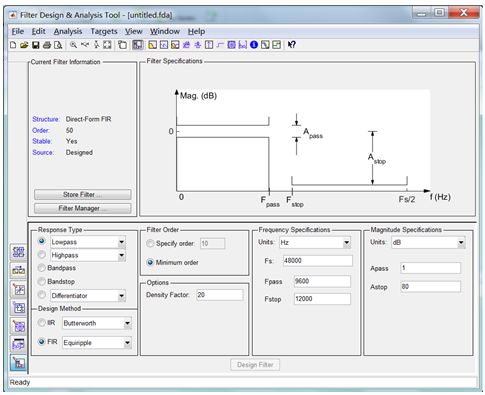
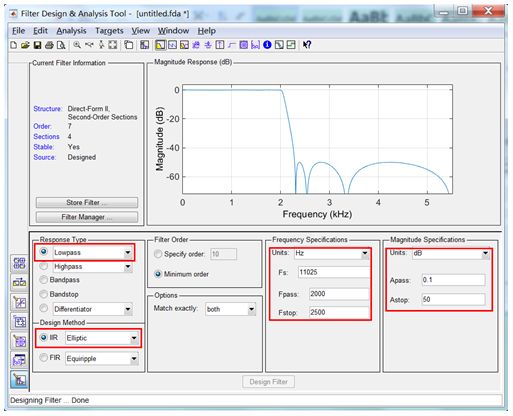
然后動動鼠標就可以完成濾波器設計了. 針對本例, 我們按下圖紅框所示設定指標, 在完成指標設定之后, 點“Design Filter”按鈕即完成設計. 關于濾波器的所有信息, 都可以通過菜單或工具欄獲得. 注意”CurrentFilter Information”部分, 它描述了當前所設計出的濾波器基本信息, 包括結構、階次、穩定性等. 有一個問題值得思考: 濾波器的結構對濾波器的工程實現有什么影響呢? 成本、穩定性、抗噪聲性能, 這些都與結構有關, 因此, 掌握濾波器各種結構的優缺點也十分重要.
很顯然, 用FDATool設計濾波器十分簡單!無論采用什么方法, 都不要忘記濾波器設計的根本目標——得到濾波器系數. 關于FDATool更多內容, 請點這里和這里.
當濾波器設計完成之后, 我們該考慮如何用所得到的系數對輸入信號進行濾波了.
-
濾波器
+關注
關注
161文章
7860瀏覽量
178928 -
信號處理
+關注
關注
48文章
1042瀏覽量
103401
原文標題:例說信號處理與濾波器設計(之二)
文章出處:【微信號:digital_signals,微信公眾號:數字信號處理輔導】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
有源濾波器中數字低通濾波器的設計及其DSP實現
MTD濾波器設計方法比較
程控濾波器的實現和濾波方案設計
詳細解析濾波器的定義,濾波器的特性,濾波器的工作原理,濾波器的分類,濾波器的典型電路原理圖

高通濾波器的定義、應用和實現方法
FIR濾波器的FPGA設計與實現
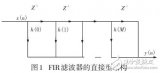
懸置線高通濾波器的設計原理和方法
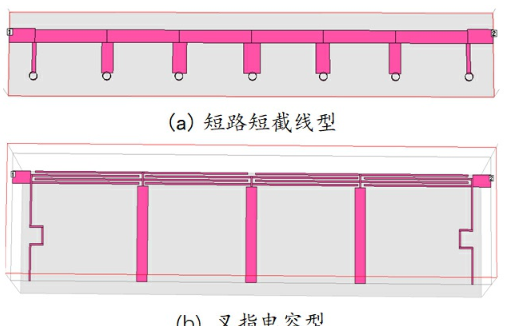




 濾波器設計征程,濾波的實現方法
濾波器設計征程,濾波的實現方法












評論