0 引言
數字抽取濾波器是ΣΔADC(ΣΔAnolog-to-Digital Converter)的重要組成部為分,旨在從高速、低分辨率的調制信號中重構出高分辨率、奈奎斯特頻率的信號。為節約硬件資源,同時滿足通帶紋波和阻帶衰減等要求,數字抽取濾波器一般采用CIC濾波器、CIC補償濾波器、半帶濾波器三級級聯方式構成[1]。本文在此結構的基礎上,對CIC濾波器部分進行優化,通過級聯結構和多相分解技術,最終有效地降低了CIC濾波器的功耗,提升了濾波器的運算速度。
為更好地驗證數字抽取濾波器的性能,本設計的輸入信號由ΣΔ調制器產生。根據640 MHz采樣頻率和64倍降采樣率,計算得到調制器最小階數為四階。經過單環、級聯結構的對比分析,最終選用四階單環前饋-反饋ΣΔ調制器。即在單環ΣΔ調制的基礎上,將第四級積分器的輸入和輸出端分別引入前饋和反饋,同時讓反饋回路作為第三級積分器的輸入[2]。在MATLAB中,使用0.5 MHz信號對該調制器進行驗證,調制器的輸出信噪比為114.7 dB。
本設計的數字抽取濾波器的目標參數為:信號帶寬5 MHz,輸入信號頻率0.5 MHz,采樣頻率640 MHz,過采樣率為64,輸出信噪比90 dB以上,通帶紋波不大于0.01 dB。
1 CIC濾波器的設計
1.1 傳統CIC濾波器
CIC抽取濾波器是一種線性相關的FIR(Finite Impulse Response,FIR)濾波器,濾波器系數均為1,結構組成只有積分器、寄存器和加法器,省去了乘法器,有效降低了硬件開銷和電路復雜度。
降采樣率為M,階數為N的CIC濾波器的z域傳輸函數為[3]:
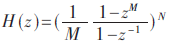
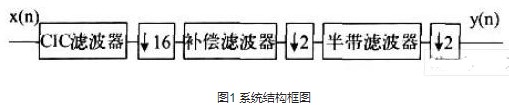
根據傳輸函數得到圖1的濾波器結構圖,此為傳統遞歸結構。
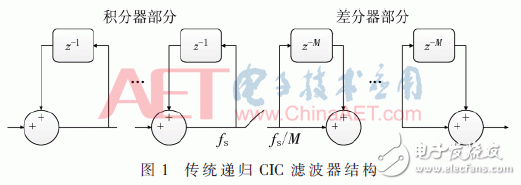
傳統結構的CIC濾波器由兩部分組成:第一部分為積分器,第二部分為差分器。可以看到,所有積分器都工作在最高采樣頻率下,導致了傳統結構功耗的增加。
芯片版圖尺寸主要由寄存器個數及位數決定,字長大消耗硬件資源多,所以CIC濾波器的輸出數據位數增長也是需要關注的一個方面。降采樣率為M,階數為N的CIC濾波器輸出數據位數由Nlog2M+Bin決定,Bin為調制器輸入位數。
1.2 多相分解CIC濾波器
為有效降低功耗,應使濾波器工作在低采樣頻率下,即讓抽取步驟在整個CIC濾波器的最前端完成,這就需要對CIC濾波器的傳輸函數進行多相分解[4]。
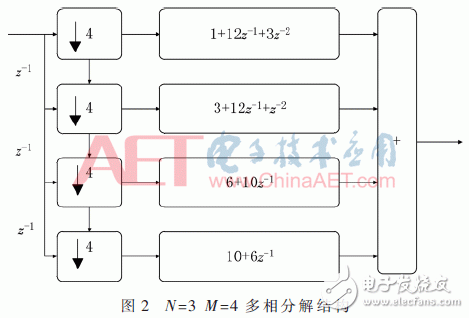
下面以N=3、M=4為例,對分解步驟進行說明,由分解后的圖2可得采樣頻率降低為fs/4。
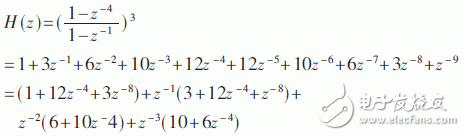
該結構中的系數相乘可以通過移位相加實現,因此只需要延時器(寄存器)和加法器,消耗資源少。通過多相分解,在一開始就進行降采樣,使后級都工作在較低的時鐘頻率下,有效降低了功耗。
1.3 CIC濾波器的結構設計
為使量化噪聲在信號帶寬內的混疊可以忽略不計,對于L階的ΣΔ調制器,CIC濾波器至少為L+1階。由四階調制器可得,本次設計應至少選用五階CIC濾波器來實現16倍降采樣。
將其分為兩級4×4級聯結構以避免一級結構過于復雜,根據Noble恒等式得:
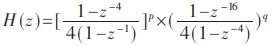
由于第一級選擇多相結構,p選取2或者3。再參考幅頻特性以及占用資源來選出最佳q值。
1.3.1 幅頻特性分析
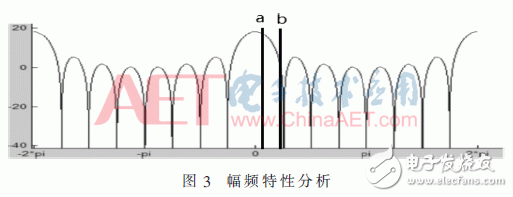
幅頻特性主要看混疊帶部分的衰減情況,因為這部分決定了總體的噪聲情況。如圖3,線a處對應通帶截止頻率,線b處對應混疊發生區域。引入帶寬比例因子β=B/Fs×M=5/640×16=1/8,計算得到a處的值為w1=β×2×π/16,b處的值為w2=2×π/16-w1。對w1、w2歸一化處理后得w1′=w1/π=0.015 6,w2′=w2/π=0.109 4。
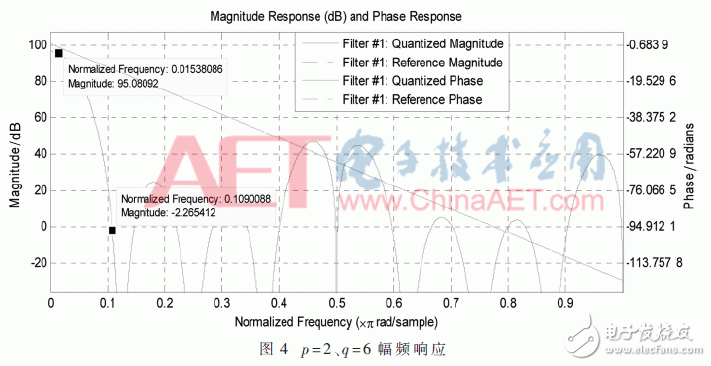
p=2時,q最小取值為6,現選取q=6、7、8進行比較,使用不同的q值進行級聯,得到對應幅頻響應圖,如圖4所示。觀察位于w1′、w2′處的衰減情況。表1為p=2時的通帶和阻帶衰減對比。

由表1可知第二級取值越大,混疊處的衰減越大,但同時基帶內信號的衰減也會增加,影響幅頻特性。當q=7時,混疊處的衰減已經滿足要求,所以p=2時,對應選取q=7。
同理p=3,q分別取6、7、8時,對應混疊區域的衰減情況見表2。

經過比較,選擇3-6結構或2-7結構。
1.3.2 加法器和寄存器分析
為了進一步確定最終結構,還需要考慮硬件消耗情況,在輸出結果符合要求的前提下,消耗較少加法器和寄存器為優。表3為2-7和3-6兩種情況下的加法器個數和有效位數。

兩種結構的衰減特性基本一樣,字長也相同,只相差一個加法器。將上述兩種結構通過SIMULINK仿真,查看結果發現,p=3,q=6結構與總的傳輸函數匹配效果更好,輸出信噪比更高。所以最終選擇p=3,q=6,其幅頻響應如圖5。
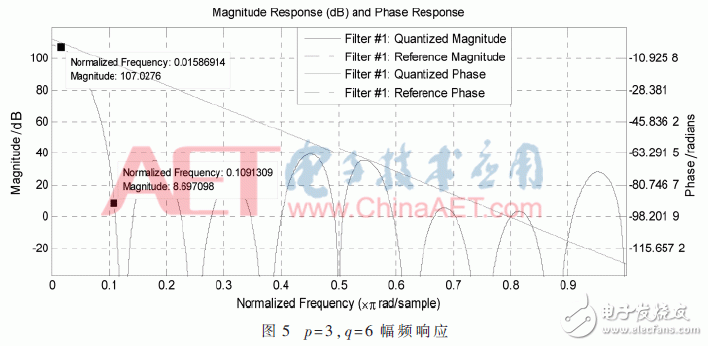
完成對上述兩部分階數和結構的選擇后,將其級聯,完成CIC濾波器整體設計。第一部分階數為3階,利用多相分解;第二部分階數為6階,選取傳統遞歸結構,最終實現高頻工作。
2 其他濾波器的設計
2.1 CIC補償濾波器
完成CIC濾波器的設計后,觀察其基帶內的幅頻響應,得到通帶邊緣處的衰減為0.2 dB。為使通帶信號平坦,滿足通帶紋波小于0.01 dB的設計要求,需在CIC濾波器后加CIC補償濾波器,對CIC濾波器輸出信號的通帶衰減進行補償。同時,CIC補償濾波器還兼顧2倍降采樣的作用。
利用MATLAB中SIMULINK模型庫中的CIC Compensator Fliter,對CIC補償濾波器進行設計。根據輸入信號采樣頻率和降采樣率,計算得:通帶頻率9 MHz,阻帶頻率11 MHz,濾波器結構選用直接型。
設計所得的CIC補償濾波器階數為72階,消耗乘法器73個,加法器72個。
通過MATLAB編程得到補償前后的濾波器幅頻響應曲線如圖6。
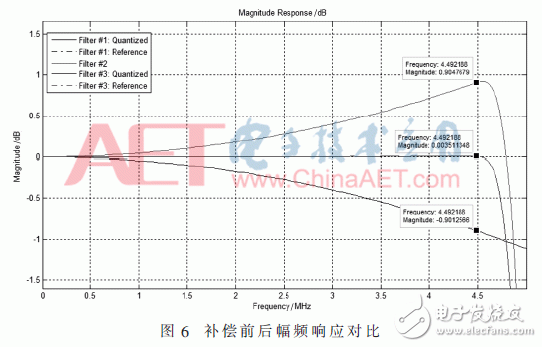
經過CIC補償濾波器后,響應曲線變得非常平,帶寬附近的通帶衰減為0.003 5 dB,達到小于0.01 dB的設計要求。
2.2 半帶濾波器
為達到阻帶衰減要求,最后一級選用半帶濾波器[5]。本次設計利用MATLAB中的“filter design”。采用“等紋波”法進行設計,結構上選取直接型結構。根據輸入采樣頻率20 MHz,降采樣率2,在濾波器設計界面中設置阻帶衰減為105 dB,計算得到過渡帶寬度為1 MHz。最終設計得到半帶濾波器的幅頻響應曲線如圖7所示。本次設計消耗乘法器65個,加法器64個。
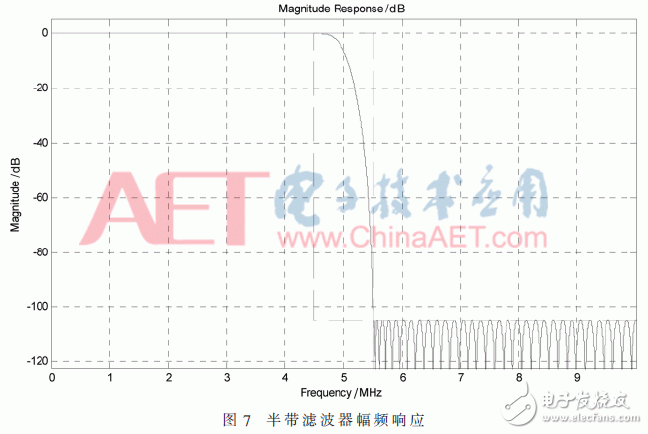
由圖7可知,濾波器的通帶和阻帶衰減均滿足設計要求。
3 仿真結果
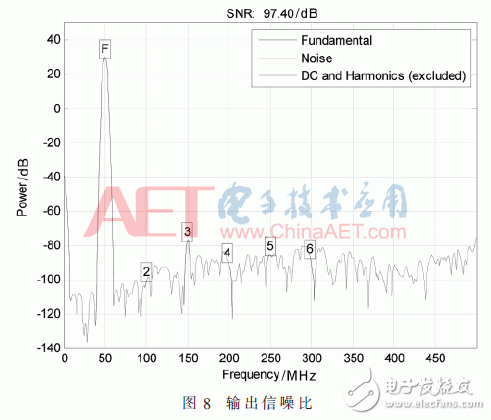
在SIMULINK Module中將上述每一子模塊搭建完成后進行級聯,輸入一個幅度為0.67 V,頻率為0.5 MHz的正弦波。將最后的輸出數據(設為a)通過To Workspace導入到MATLAB中,在MATLAB命令行中執行snr(a),計算輸出信號信噪比,得到整個ΣΔ模數轉換器的輸出信噪比為97.40 dB,如圖8所示,計算得到分辨率為16位。
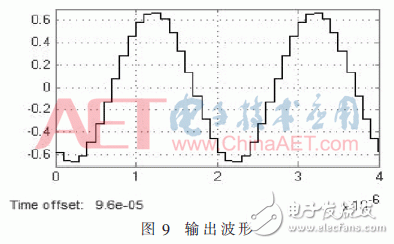
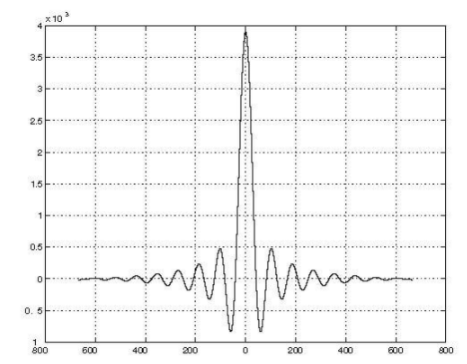
為進一步驗證數字抽取濾波器的輸出結果,使用示波器觀察輸出波形。選擇SIMULINK中的scope模塊,輸入相應的時間范圍,本次設置選擇顯示兩個時間周期。得到輸出波形如圖9所示,可以看到輸出維持了輸入正弦信號的趨勢。
4 結論
本論文以降低功耗為目的,對工作在高頻信號下的數字抽取濾波器結構進行設計。利用多項分解優化了CIC濾波器結構,并搭建了四階調制器,利用MATLAB軟件對其進行功能仿真。最終仿真所得各項結果均滿足設計要求。
-
濾波器
+關注
關注
161文章
7860瀏覽量
178929
發布評論請先 登錄
相關推薦
求助,AD7190關于Σ-Δ ADC其中的抽取濾波器的數據轉換問題求解
數字濾波器設計
數字下變頻中抽取濾波器的設計及FPGA實現
以FPGA為基礎的Σ-? 轉換中抽取濾波器的設計過程詳解
基于FGPA實現數字下變頻器的抽取濾波器設計方案詳解
FPGA的FIR抽取濾波器設計詳細教程
FPGA的FIR抽取濾波器設計教程
如何使用FPGA實現FIR抽取濾波器的設計
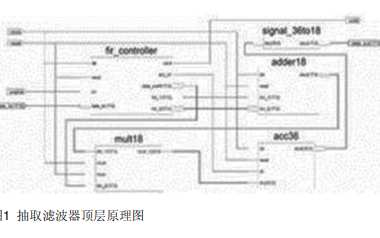
關于抽取和插值濾波器的介紹
基于FPGA的_ADC數字抽取濾波器Sinc_3設計





 關于高頻數字抽取濾波器的設計
關于高頻數字抽取濾波器的設計











評論