Abstract：串擾是SI設計中較為重要的一個概念，如何在產品設計中保持信號在傳遞過程中不會受到周圍信號的影響，同時不會影響到其它信號線，是確保產品順利通過測試的關鍵。串擾的產生，主要是由于相鄰傳輸線間的互電容（Mutual Capacitance）和互電感（Mutual Inductance），這些分布參數使信號在傳遞過程中將自身攜帶的電壓電流信息部分耦合到相鄰的受擾線（Victim line）上。目前常用的抑制串擾的手段，均是采用降低線間的分布參數的原理。如簡單的拉開線間距（常見的3W原則）、加防護線、防護地孔等；對于線束間存在的串擾，通常會通過雙絞、屏蔽等方式降低串擾幅值。本文將詳細介紹這幾種常見措施的效果及差異，希望通過不同角度的分析，讓讀者了解產品設計中的一些方法。

目錄

Crosstalk

1、近端串擾和遠端串擾

2、串擾模型的建立

3、耦合長度對串擾的影響（多重crosstalk）

4、間距變化對串擾的影響（3W原則由來）

5、防護地線對串擾的影響（Guard Trace Effect）

6、防護過孔對串擾的影響

7、Minimization of Crosstalk

8、ANSYS串擾檢查模塊

9、線纜間的串擾

參考

1、近端串擾和遠端串擾

串擾是由一條線到另一條線的能量耦合引起的，耦合的方式主要分為電場（electric field）和磁場（magnetic field）。由于走線之間存在著互容（Mutual capacitance）和互感（Mutual inductance），一條走線上的AC信號便會從這些分布的互容和互感傳遞到另一根被擾線（victim net）上。

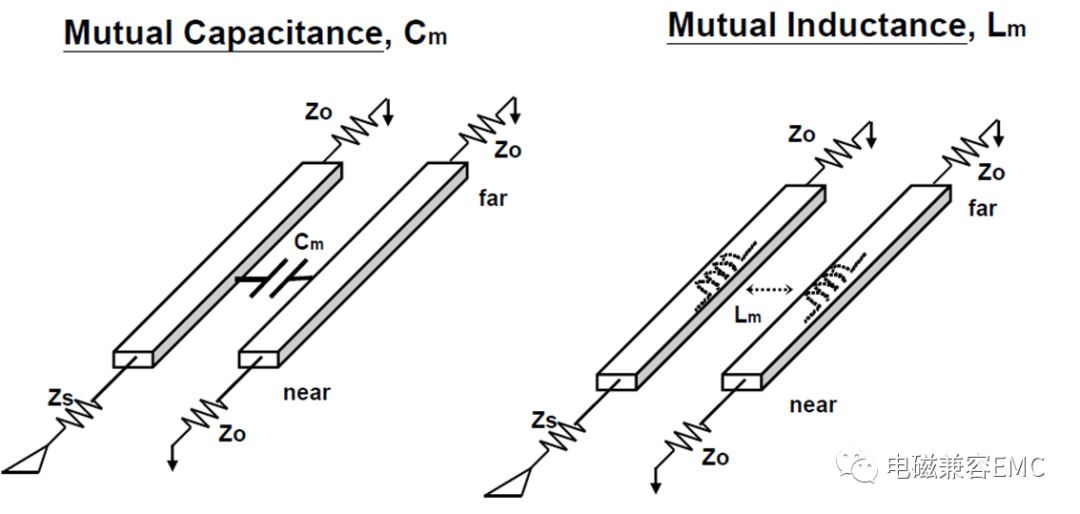
Fig1. Mutual Capacitance and Mutual Inductance

1.1互感

互感通過磁場將噪聲電流從一條驅動線引導到相鄰的被擾線上，驅動線產生的磁力線穿過被擾線上，行成感應電流。

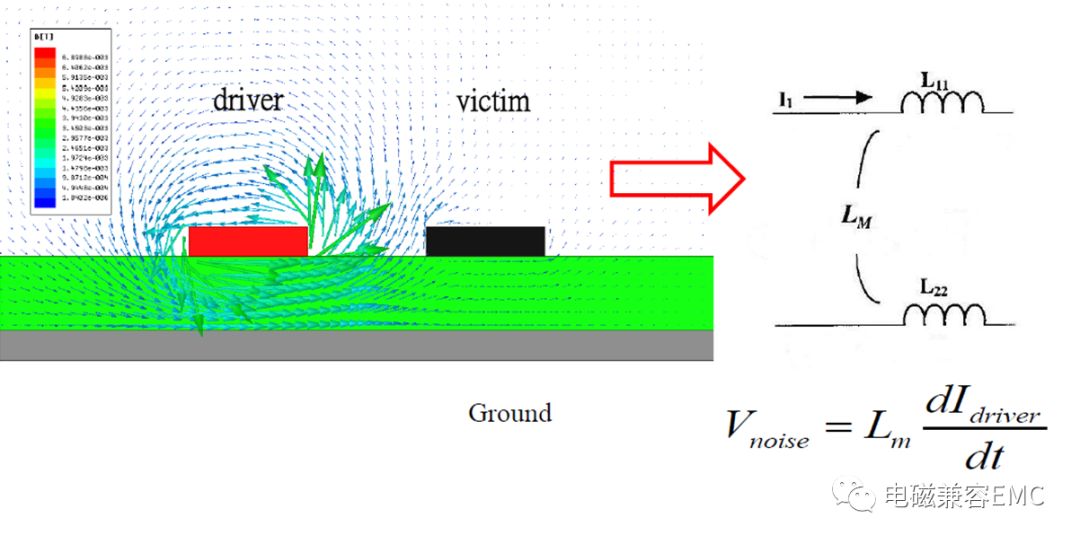
Fig2.Mutual Capacitance

1.2互容

是兩導體間通過電場耦合，驅動線上的時變電壓信號通過互容在被擾線上引起感應電壓。

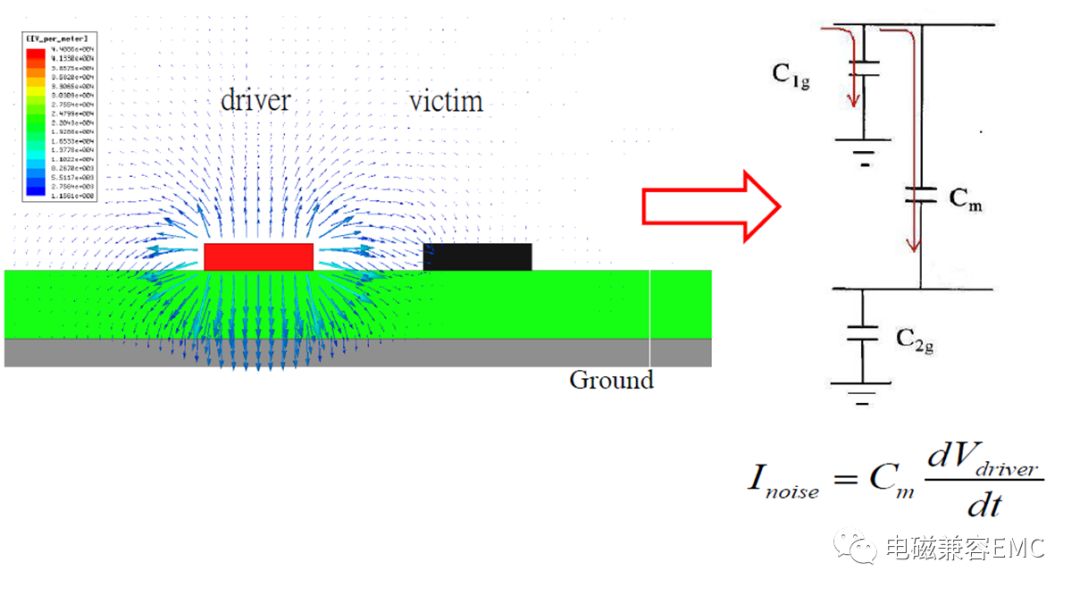
Fig3.Mutual Inductance

1.3 近端串擾和遠端串擾

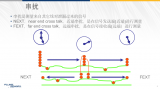
如圖1所示，現實中為了測量串擾幅值，會分別測受擾線兩端的噪聲情況，為了區分這兩個末端，把距離源端最近的一端稱為“近端”，而遠離源端最遠的一端稱為“遠端”。這兩端也可以用信號傳輸的方向來定義，即遠端是信號傳輸方向的“前方”，近端是信號傳輸方向的“后方”。在受擾線（victim line）上耦合的噪聲分為電流噪聲和電壓噪聲。下圖為耦合在victimline上噪聲電流的示意圖，NEXT近端耦合電流為互感耦合電流與互容耦合電流的和，相反，FEXT遠端耦合電流為互感耦合電流與互容耦合電流的差。

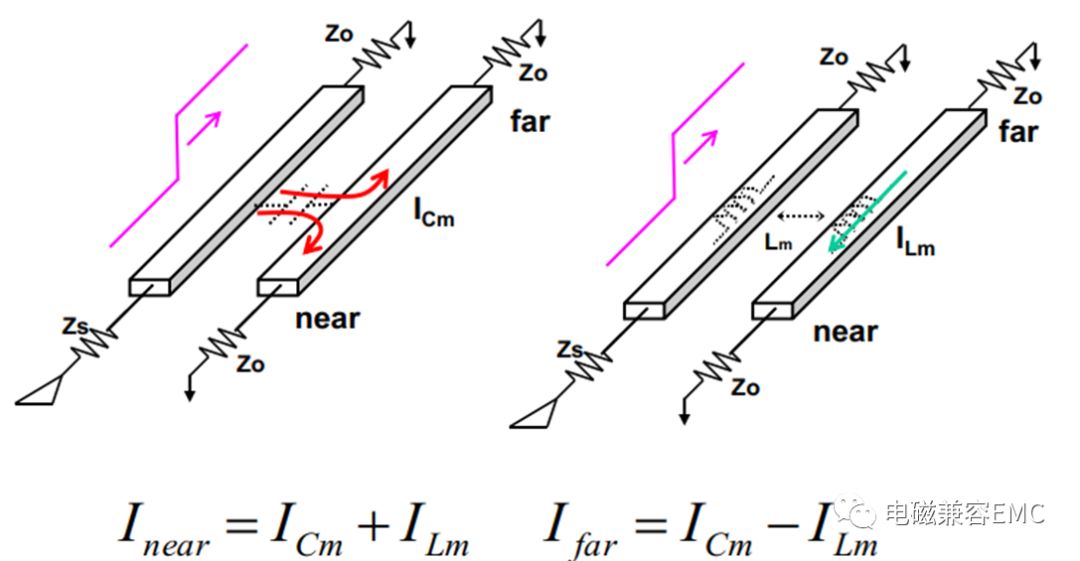
Fig4. Coupled Currents

下圖為電壓耦合示意圖，從圖4中可知，近端串擾為互容和互感電流之和，所以近端串擾的電壓幅值總是正的。而遠端串擾為互容和互感電流之差，所以遠端串擾不總是負的。其中原因有兩個：

Lm的電流大于Cm電流情況

遠端為開路的情況下

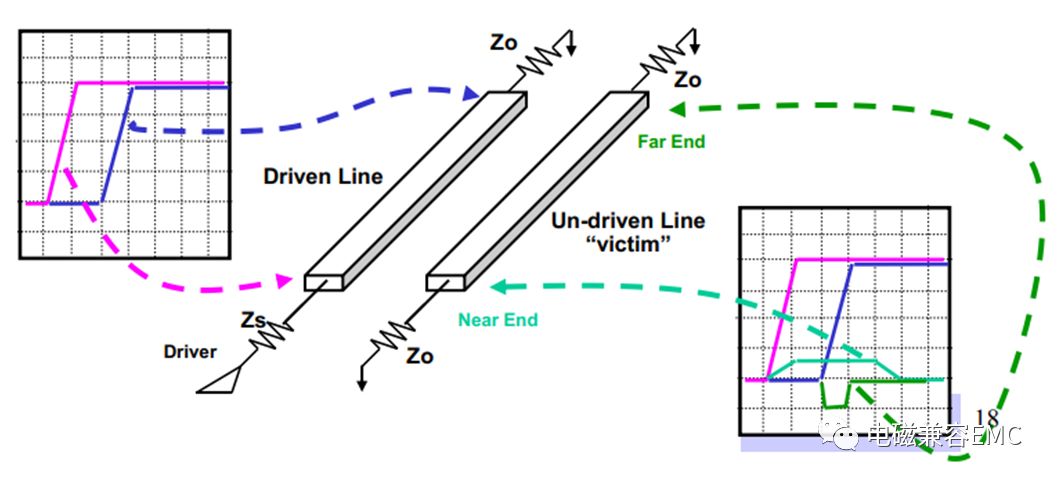
Fig5電壓耦合示意圖

近端和遠端耦合電壓的描述，下圖吳瑞北老師的課件中給出了三種情況下，近端和遠端的串擾模型及相應的計算公式。從中可以看出，近端耦合噪聲幅值僅與微帶線分布參數和驅動電壓有關，當耦合微帶線截面尺寸和驅動電壓電平確定，其幅值便可以確定。而遠端耦合噪聲的幅值，不僅與微帶線分布參數和驅動電壓相關，還受時延與驅動波形上升沿時間相關。

Driver pluse在quiteline近端造成一個較長的耦合信號，該信號開始于0時刻，持續時間為2Td，近端串擾信號隨著驅動器上升邊沿逐步上升，當信號前沿傳輸了一定長度后，近端的電流將達到一個穩定值不再增加，該長度稱為飽和長度。傳輸線飽和長度Len為：

其中為信號上升時間，v為信號在driver line中的傳輸速度。

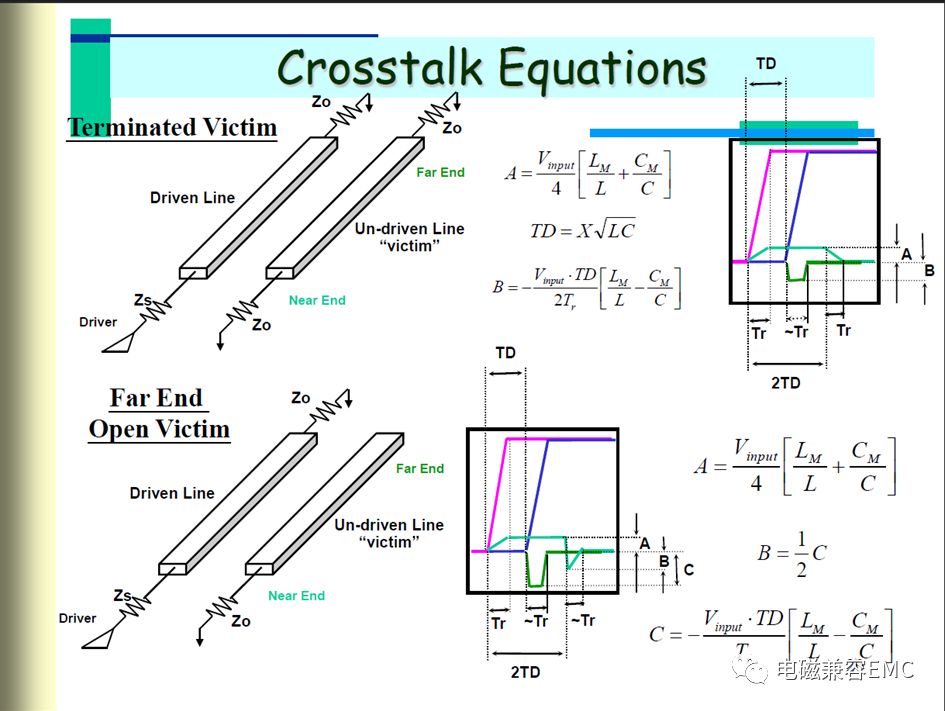
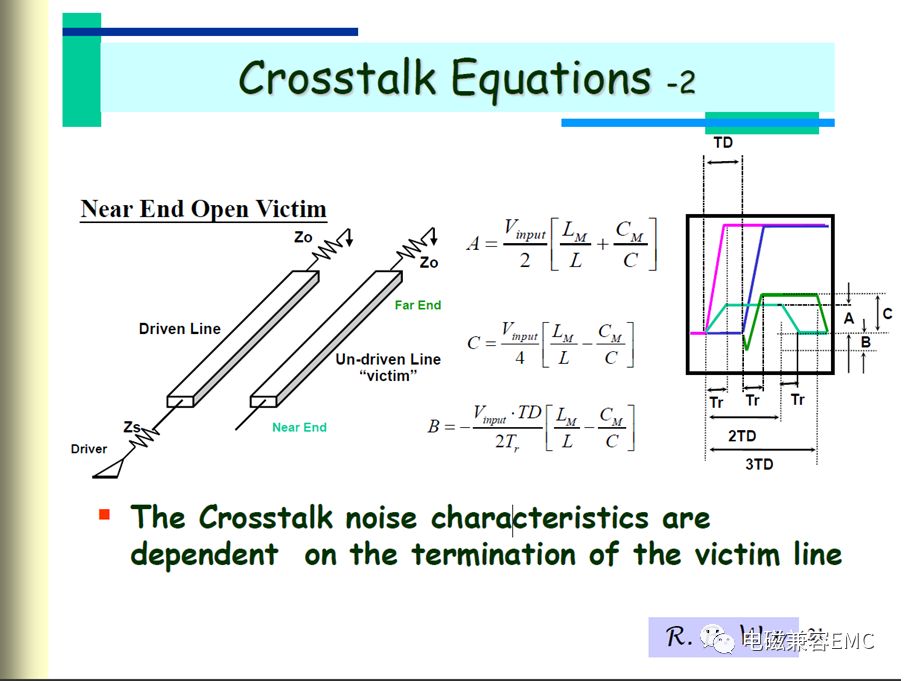
Fig6 NEXT和FEXT波形及幅值計算

2、串擾模型的建立

因為現實中不存在理想傳輸線，所以無法實現理想情況下的阻抗匹配，因此可以說反射無處不在。反射的存在，使串擾的分析變得復雜。因此為了降低其影響，需要對所建立的模型進行阻抗設計，盡量降低反射的幅值。

2.1 采用ANSYSMicrostrip-CPL工具進行特征阻抗設計

如圖1所示，建立端口特征阻抗為49.93Ω的耦合微帶線，線寬為0.25mm，距離GND平面高度為0.14mm，介電常數為4.4，長度為50mm。

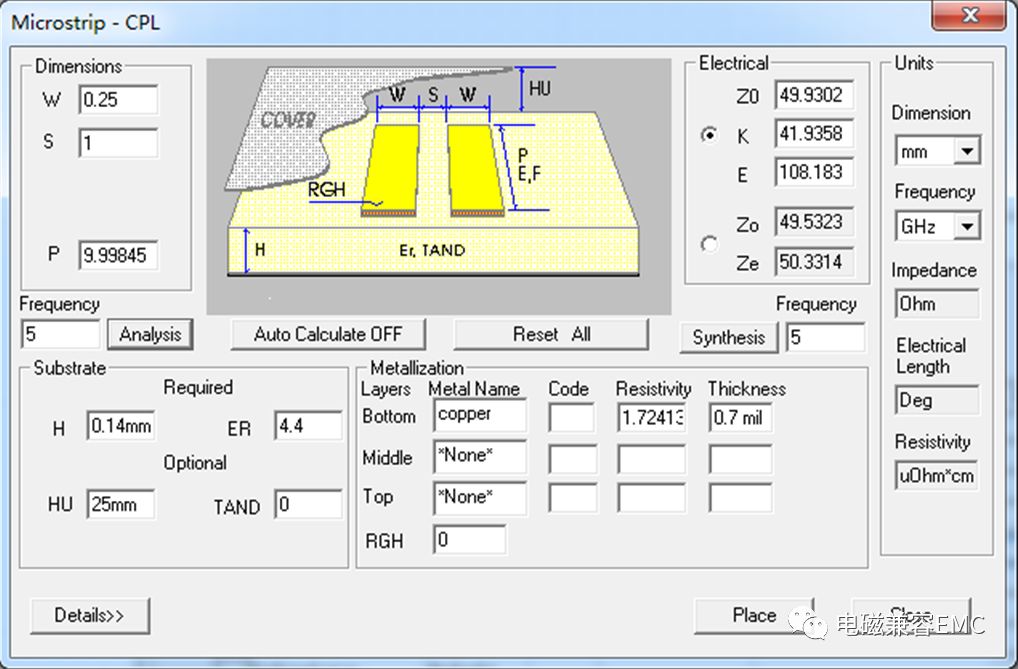
Fig7.特征阻抗為49.93Ω的耦合微帶線參數

根據前面參數在designer中建立仿真模型，2號微帶線為driver line，1號線為victimline，Vo為輸出電壓，NEXT為近端串擾電壓，FEXT為遠端串擾電壓。

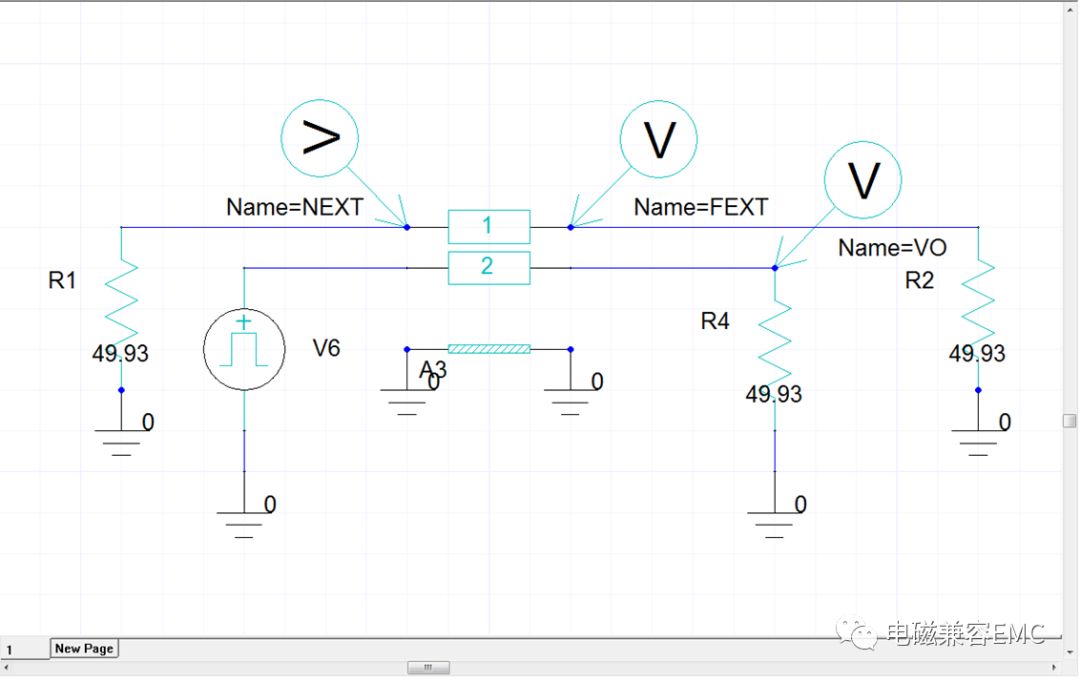
Fig8.耦合微帶線仿真模型

Driver line上驅動信號波形為，電壓幅值1V，TR=20ps，TF=20ps，PW=200ps的單脈沖方波。圖3為VO端的輸出波形，從中可以看出幾點，首先傳輸線產生了18mV的壓降。其次，m3-m4間有9.5mV的凸起，這個是脈沖的二次反射，三次以上的反射因為幅值太小已經無法觀察到。

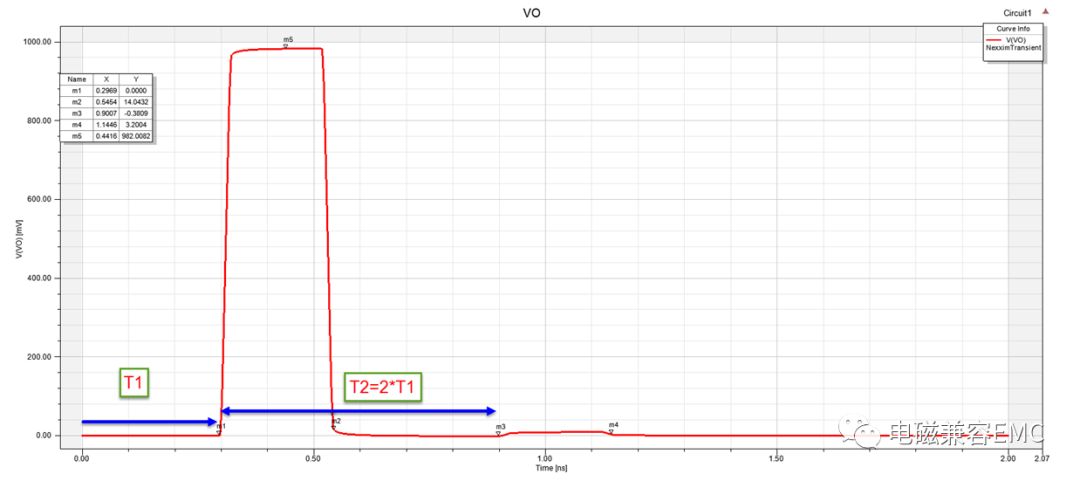
Fig9.VO端輸出波形

2.2 Delay-time

圖3的結果中可以看出，信號在該耦合微帶線上的傳輸時延約為297ps，這里用Polar驗證一下不同軟件算出的傳輸線時延是否吻合。選擇Edge-Coupled Coated Microstrip 1B計算模型，如圖4所示，可以看出Delay-time結果為5.938ps/mm，乘上微帶線長度50mm，總的時延為5.938*50=296.9ps，與圖3的結果完全吻合。

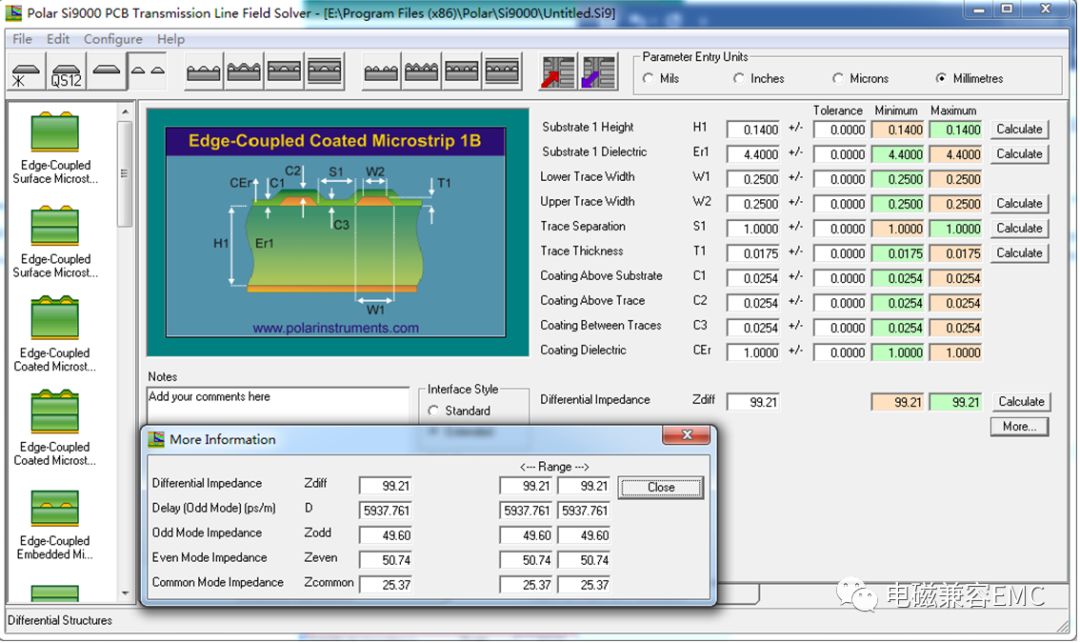
Fig10.同樣參數下Polar計算出的阻抗和時延結果

2.3 近端串擾NEXT和遠端串擾FEXT

從圖2中可以看出，Victim line與Driver line同樣進行了阻抗匹配。圖5中可以看出近端和遠端接收到的波形情況，由于幅值較小，這里分別對NEXT曲線乘25倍，對FEXT乘2倍處理，以便觀察。結果中可以看出，近端串擾幅值為4mV，遠端串擾幅值為93mV。

觀察NEXT波形，可以看出波形從0s開始上升，這是由于Victim line近端可以第一時間接受到來自Driver line的噪聲信號，在這段時間內，波形還未到達傳輸線末端，認為FEXT端開路，NEXT端為短路，ICM+ILM為正，所以其電壓幅值為正。而當過了594ps后，NEXT端迎來了FEXT端傳過來的二次反射，這時從FEXT端看進去的情況剛好相反，所以電壓波形為負。

觀察FEXT波形，可以看出波形從297ps時開始下降，這時Driver line電壓波形剛好開始上升，此時傳輸線末端為短路，近端是開路，ICM-ILM為負，所以接收到的電壓波形為負值，當時間在320ps~520ps時，由于不存在dV/dt，所以沒有感應電壓產生。當Driver line電壓波形下降時，FEXT端接收到相反的dV/dt，所以電壓波形為正。

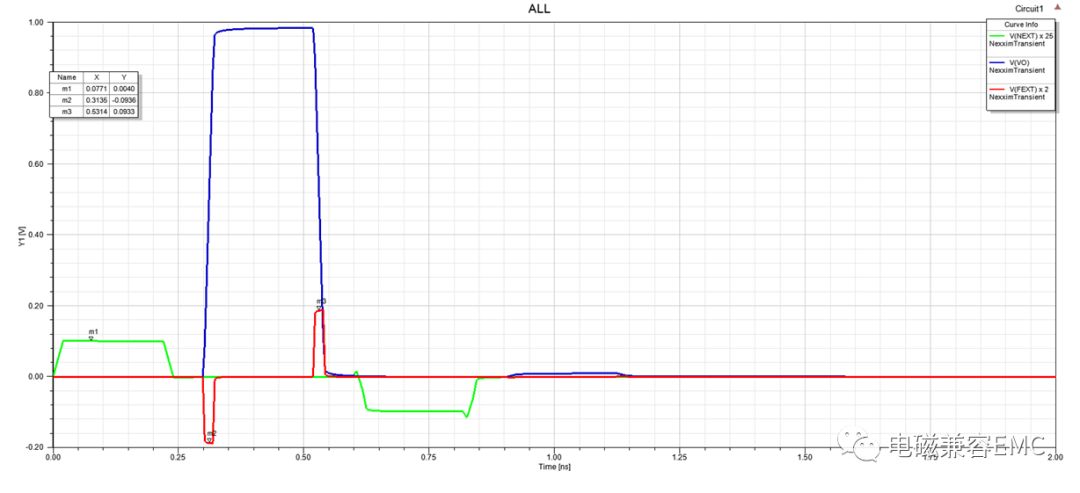
Fig11.NEXT和FEXT與VO的電壓波形

3、耦合長度對串擾的影響（多重crosstalk）

沿用第二節中微帶線的參數，其中線間距SP設置為0.25mm，微帶線長度設為L，sweepL 10mm~150mm per 10mm，查看三個電壓波形。

3.1、疑問？

通常我們認為遠端串擾寬度與pluse的上升沿和下降沿時間相等，均為Tr不變（20ps），而且隨著耦合長度增加，遠端串擾的幅值也應該隨之增加。但下圖中可以看出，隨著平行走線超過50mm，FEXT的大小卻呈現飽和（476.7mV），并且pluse寬度增加（＞20ps），這是為何？

Fig12FEXT端電壓波形

3.2、原因分析

為了找出FEXT隨著耦合線增加，其感應pulse的高度卻在某長度不再增加的原因，我們觀察一下Vo隨著耦合線長增加的波形變化，如下圖所示，physical length 50mm以上（含）時，Vo的rising/falling在一半高度開始有變化。

Fig13Vo端電壓波形

假設：activeline上的pulse Vi對quiet line感應的FEXT電壓又返回來對原active line上正在傳遞的該pulse信號產生影響，即第一次的FEXT對active line產生二次耦合（FEXT）。那這個問題不管怎么調active line或quiet line上的終端電阻都沒有用，唯有拉開space或將stack-up變薄以降低crosstalkeffect才有效。

那么，實際上是否如假設說的一樣呢？下圖采用傳輸線模型描述了微帶線間的耦合原理，我們用特征阻抗Z來代替復雜的分布電容和分布電感參數，可以看出active line與quiet line組成的微帶線系統，其共模阻抗為50，差模阻抗約為100。在微帶線長度為無限長時，認為其為完全耦合，此時，電路模型采用集總參數描述，分配到quiet line末端電壓的幅值恰好為active line的1/2，這也就解釋了為何FEXT端飽和電壓幅值約為Vo的1/2。

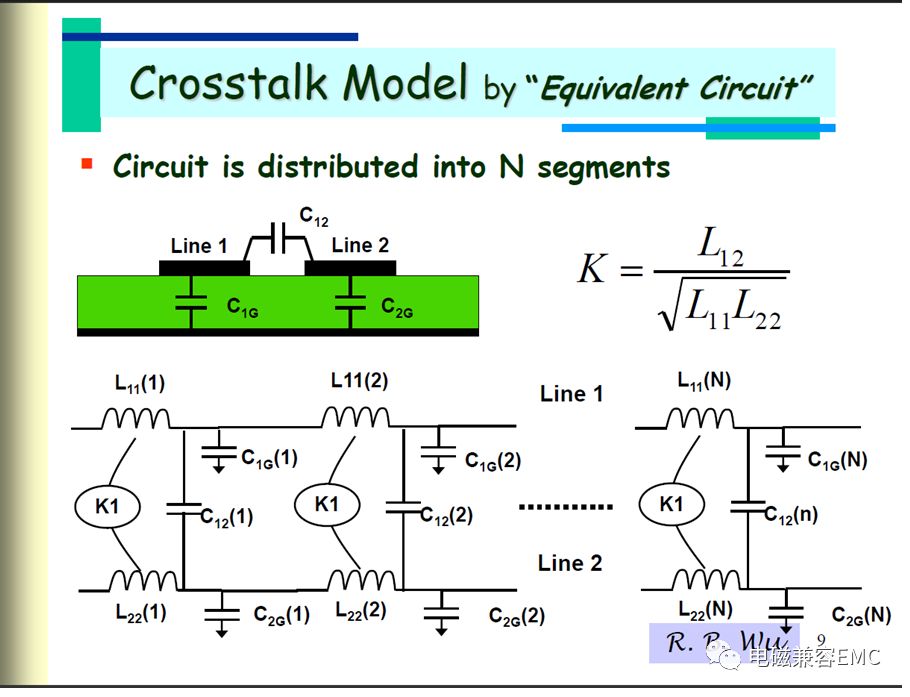
Fig14采用傳輸線理論描述的耦合微帶線模型

因為耦合微帶線采用的是傳輸線模型計算，不能單純的以集總參數描述它們之間的行為。下面建立多節傳輸線模型，研究信號在傳輸中的變化過程。微帶線截面參數與上面保持一致，單節模型長度為20mm，總長度100mm。

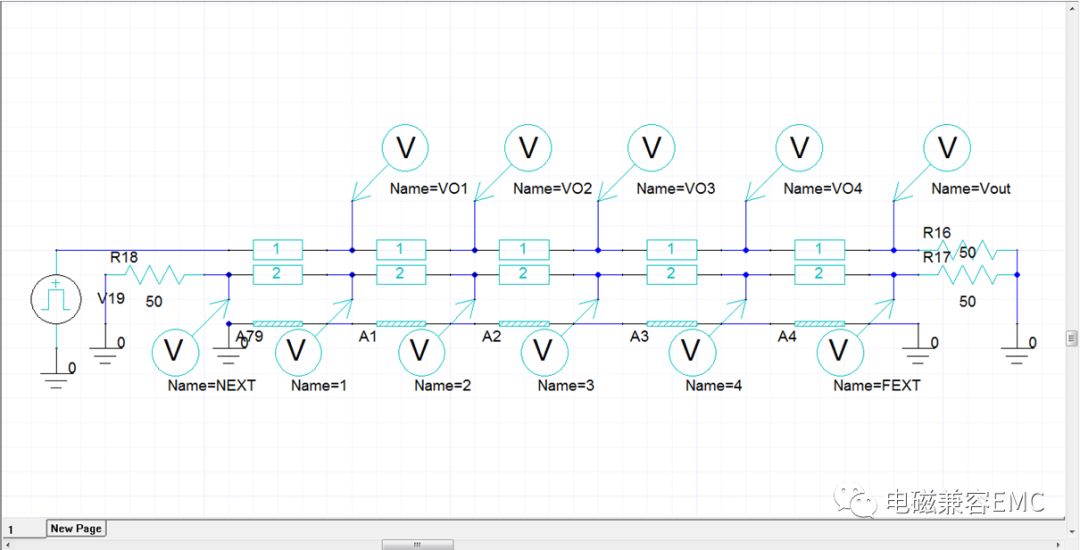
Fig15傳輸線上信號變化過程

下圖為每節active line輸出波形與quiet line感應波形，從中可以發現，輸出波形隨著出，隨著長度增加，波形上升沿和下降沿時間加長，橫電平時間幾乎不變。按照理想傳輸線中信號傳輸速度來看（下式），速度僅與介質有關，與頻率無關。所以這種變化是不該出現的。

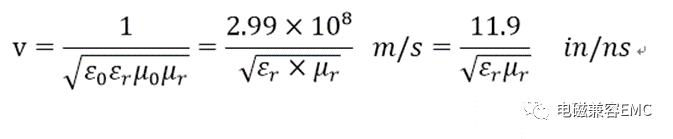
實際有耗傳輸線中會產生色散，因此上升沿與下降沿中對應的高頻成分，會隨著傳輸距離的增加，產生比低頻成分更多的衰減。所以，隨著傳輸距離的增加，上升沿和下降沿會趨于平緩。因為這里采用單個矩形波脈沖信號，當信號為連續脈沖時，退化的邊沿會與后續的波形疊加，此時，信號的寬度不變，疊加會導致更嚴重的震蕩產生，導致信號波形惡化。

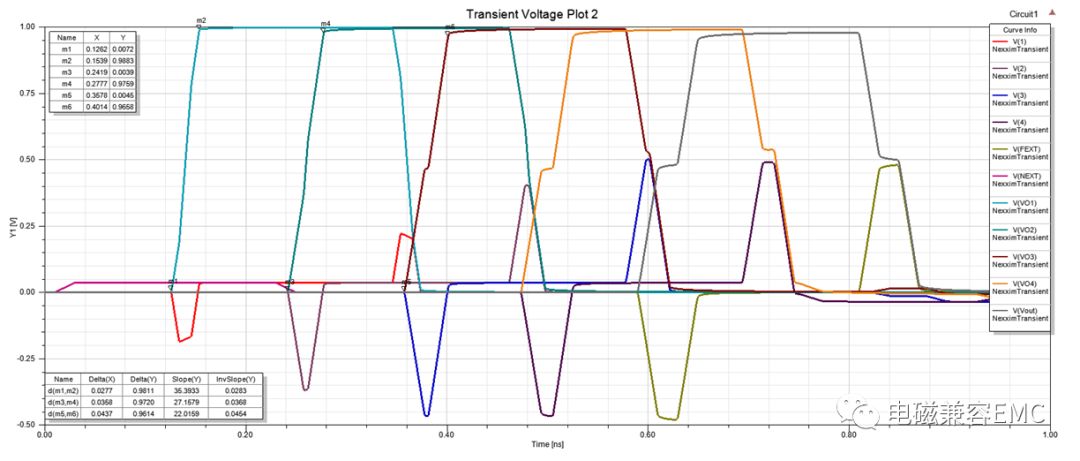
Fig16單節傳輸線上的波形分布

仔細觀察圖16，可以看到NEXT端波形為正，而V1波形為負，V1是否存在一個臨界值？答案是否定的，當信號開始進入active line，quiet line上便會第一時間感應出負電壓，隨著距離增加，負電壓持續時間增加。當信號傳遞到傳輸線飽和長度時，負電壓持續時間開始與信號上升沿時間相等。下面我們驗證該結論，采用SI9000計算信號時延為5.745ps/mm，時延與傳輸速度呈倒數關系。所以傳輸線的飽和長度為：

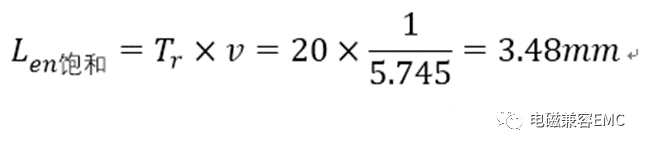
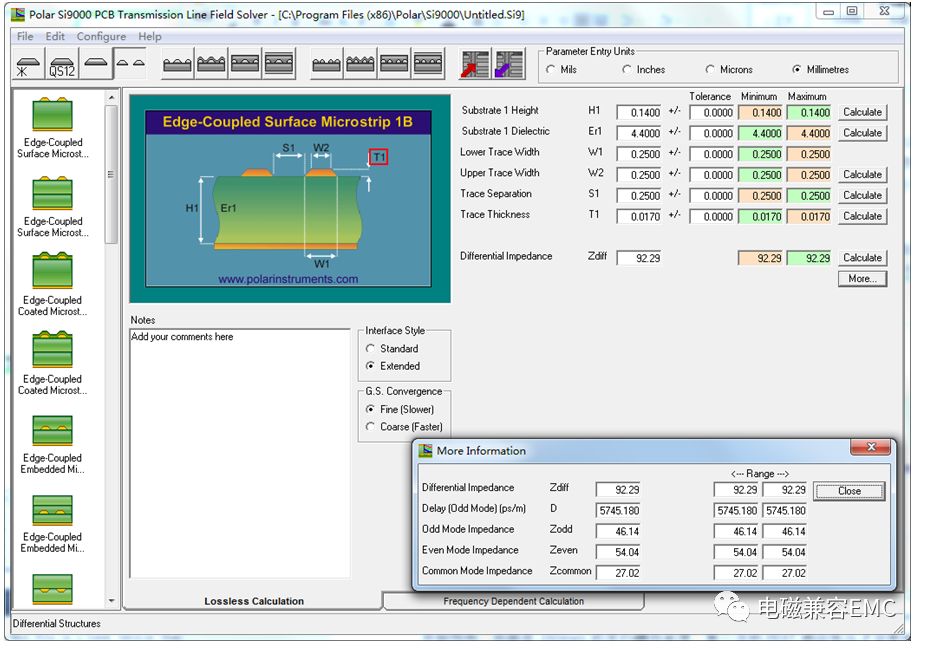
Fig17耦合微帶線模型的時延

當把第一節傳輸線模型長度調整為3.48mm時，V1端電壓波形在負電平時間恰好為20ps，第一章中指出，飽和長度的定義為近端串擾電流達到穩定值對應的長度，這里延伸到遠端，也指遠端電壓持續時間達到與上升沿時間相等，且不再增加的長度。

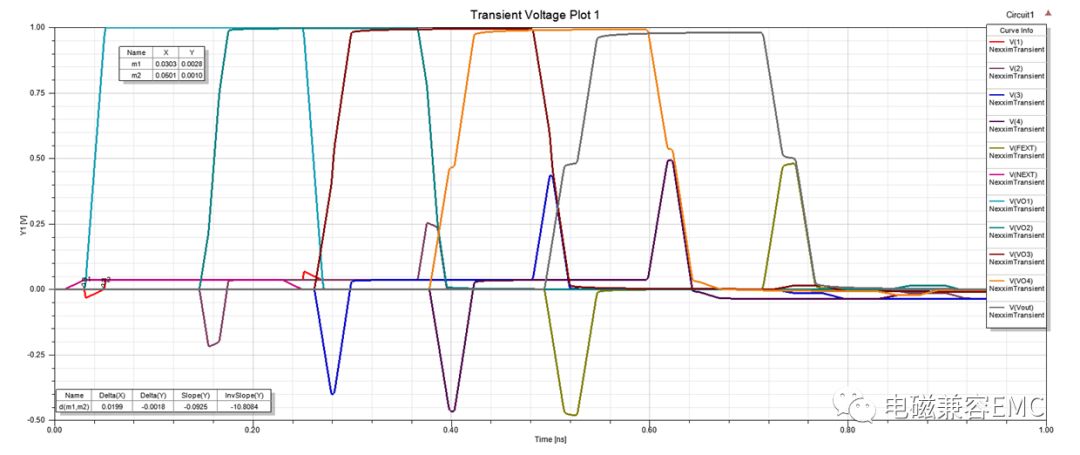
Fig18飽和長度位置下的耦合電壓波形

3.3、二次反射的情況

查看3.1節中NEXT端波形情況，可以看出只有當傳輸線長度為10mm時，電壓波形寬度是小于20mm以上情況的。由3.2節可知，傳輸線時延為5.745ps/mm，當長度為10mm時，耦合波形時間長度為57.45ps。而結果中m1~m2對應的時間為117ps，這是為什么呢？

隨著傳輸線長度的增加，二次反射回來的波形出現了明顯的塌陷，這種情況產生的原因與3.2節中FEXT情況是一樣的。

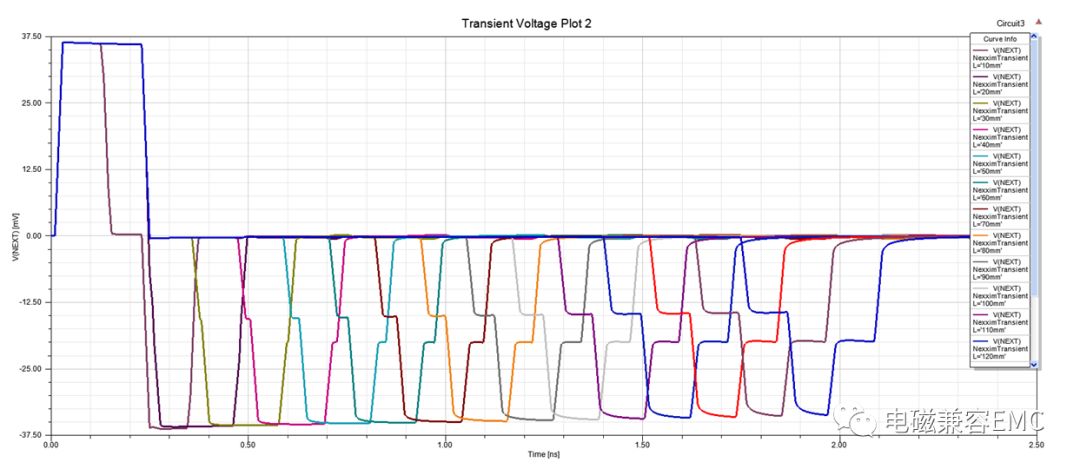
Fig19NEXT端電壓波形隨長度變化情況

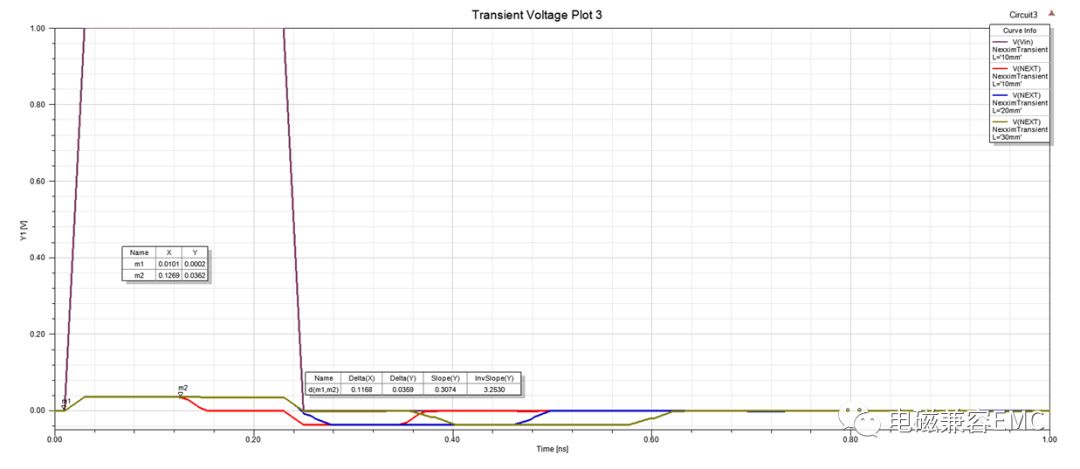
Fig20NEXT端電壓波形和active line輸入波形

3.4、active line和quiet line參數調節

在3.1的基礎上，同樣的仿真參數再跑一次，但把active line與quiet line的距離由0.25mm修改為0.75mm，我們發現NEXT、FEXT都變小，且當physical length增加到160mm時，FEXT才開始飽和，也就是160mm的平行耦合長度，第一次的FEXT感應電壓才會影響原active line上正在傳遞的pulse信號。

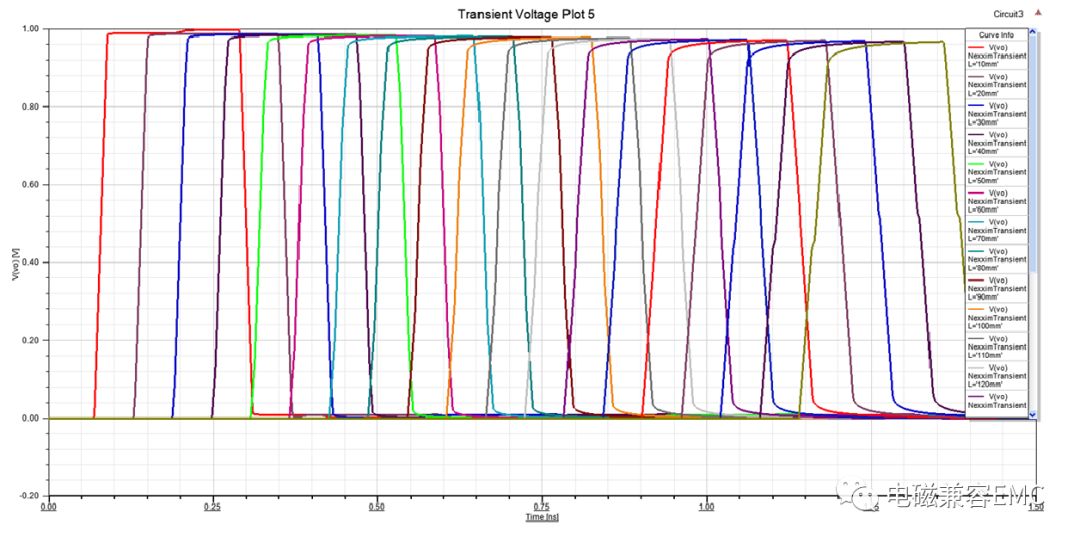
Fig21拉開距離后的輸出電壓波形

4、間距變化對串擾的影響（3W原則由來）

在第二節中，仿真模型默認間距S為1mm，線寬W為0.25mm，這里我們調節線間距S，以0.25mm為倍數，S的值從1W增加到5W，查看受擾線上NEXT和FEXT串擾幅值的變化規律。從圖6和圖7和圖8中可以看出，隨著間距增加，NEXT和FEXT端串擾電壓幅值先是快速下降，隨著S繼續增加，下降趨勢放緩。

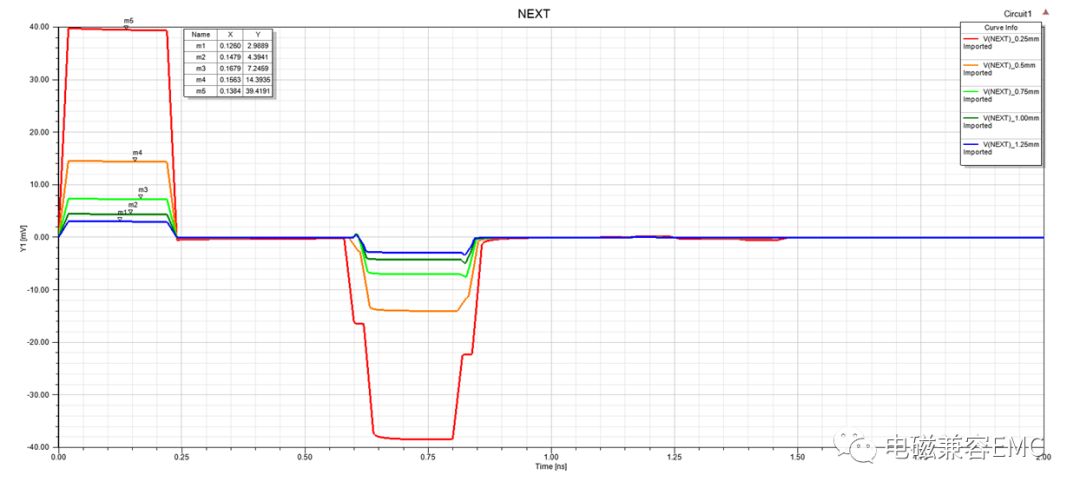
Fig22.NEXT端串擾幅值隨S變化情況

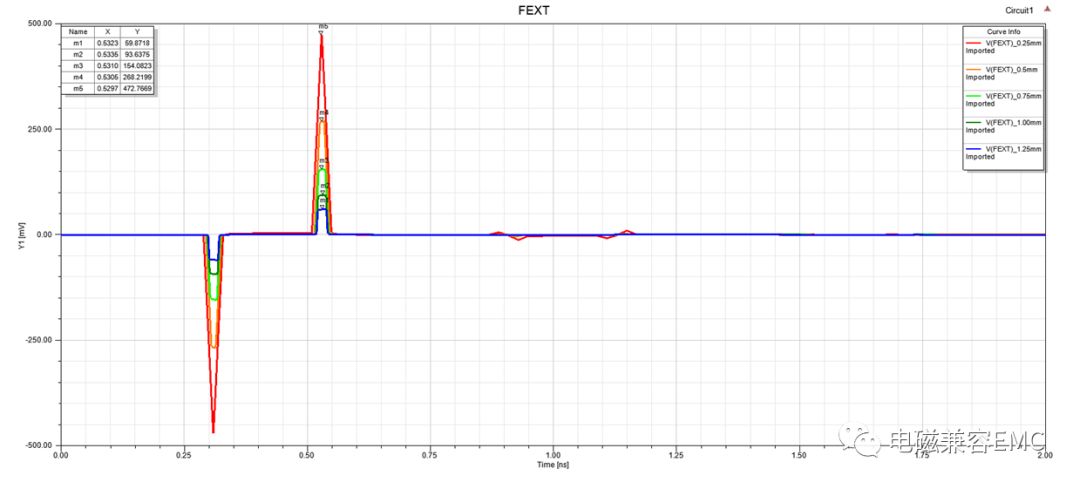
Fig23.FEXT端串擾幅值隨S變化情況

我們所熟知的crosstalk 3W rule一般是指：在特性阻抗50Ω下的傳輸線，保持3W的間距是安全的。對于特性阻抗高于50Ω的情況，3W的間距往往是不夠的。

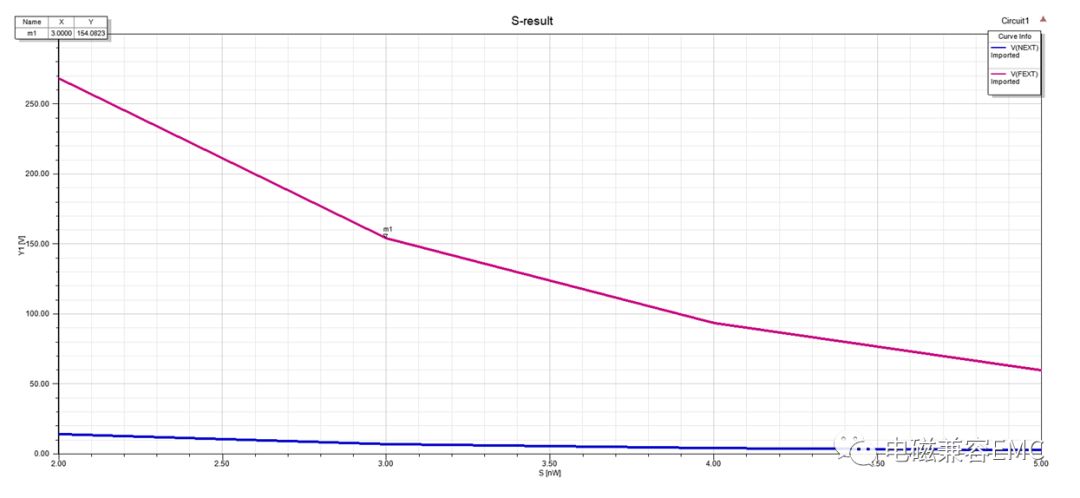
Fig24.Victim line隨S增加，兩端接收到的crosstalk電壓走勢

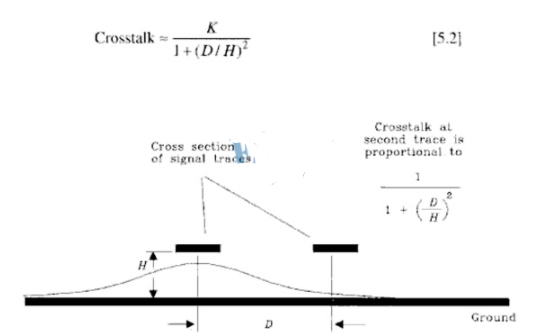
下面是Montrose 在《Printed Circuit Board Design Techniquesfor EMC Compliance》一書中對3W原則的描寫

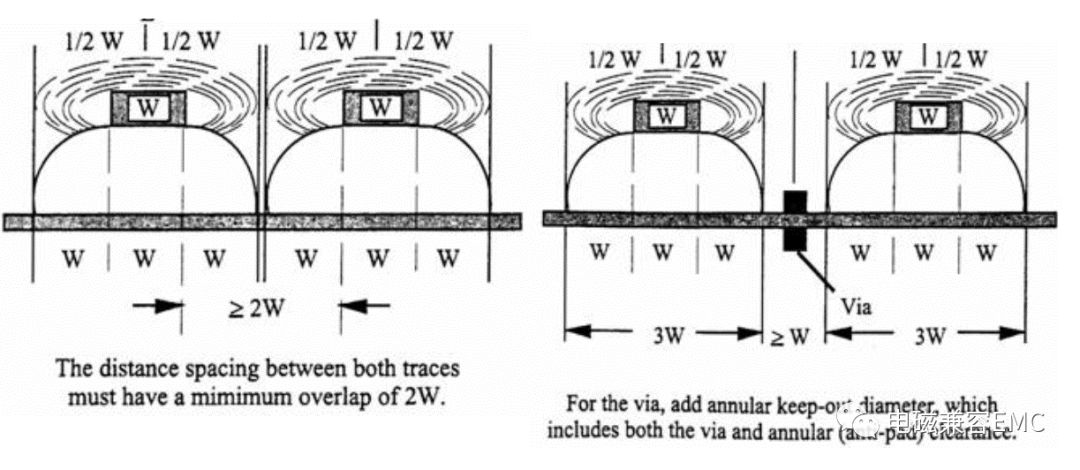
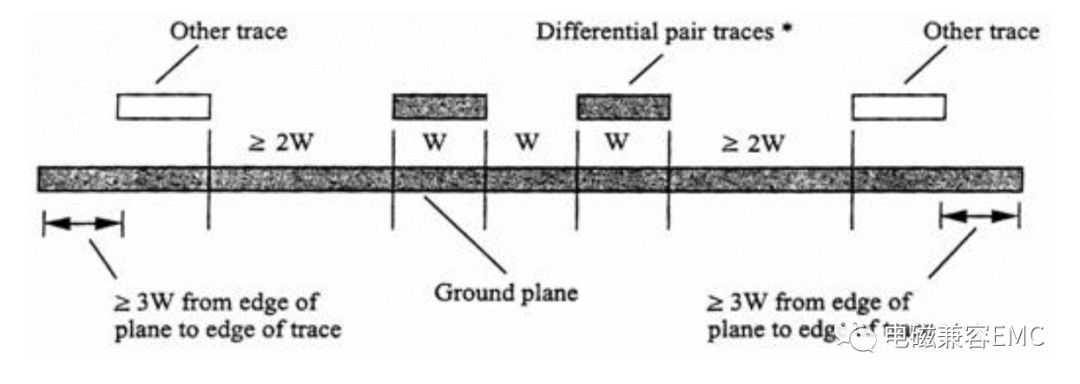
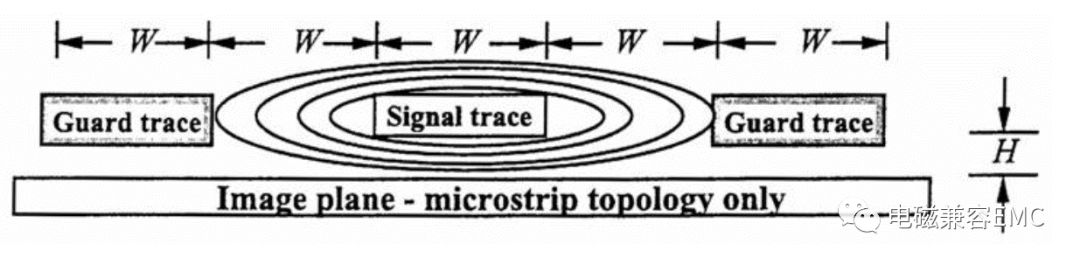
5、防護地線對串擾的影響（Guard Trace Effect）

從PCB設計的角度講，敏感信號線間除了需要保持一定的距離，往往在設計時會考慮加入防護地線，進一步保護走線不被影響。防護線的作用主要是引入低阻抗邊界，將信號線上發射出來的電力線引入到地回路。下面用ANSYS對防護線進行仿真，查看其對串擾的影響。

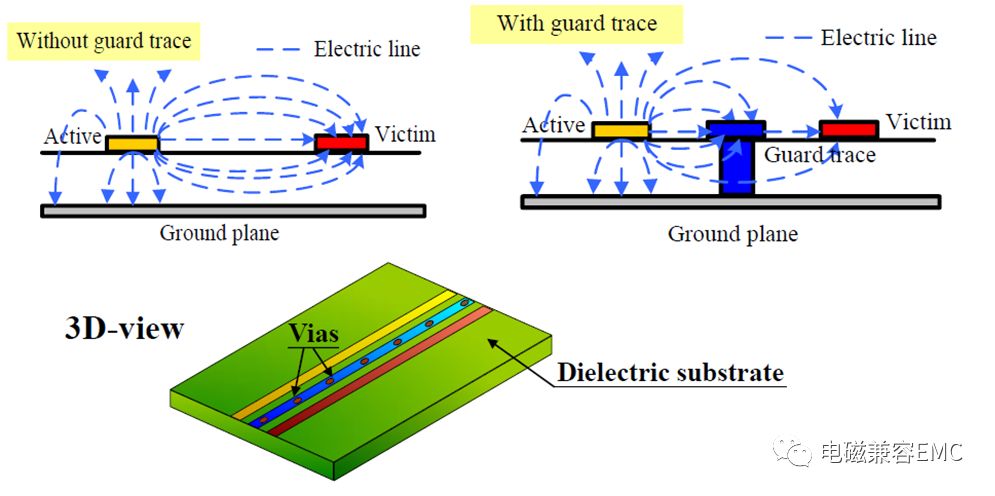
Fig25.With/withoutguard trace

5.1固定線寬下，防護地線的影響

下圖走線線寬7mils、線距7mils（走線邊緣到邊緣）、過孔直徑5mils、ground guard trace線寬10mils、線長50mm，板厚1.6mm；分別是走線不伴隨地線、兩條走線伴隨一條地線、四條走線伴隨一條地線。

5.1.1 兩條線穿插一條地線

圖26中所示模型，走線編號從上到下分別為T01~T09，每條trace的左側為L端口，右側為R端口，圖27為每條trace的S21參數。

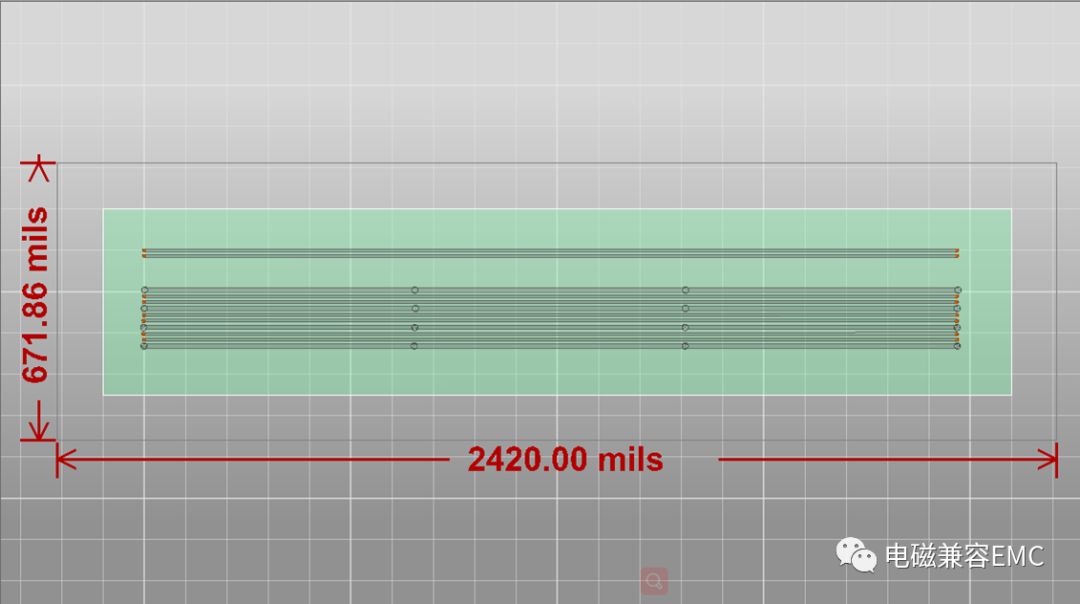
Fig26.兩條線穿插一條地線

Fig27. S-parameters for S21

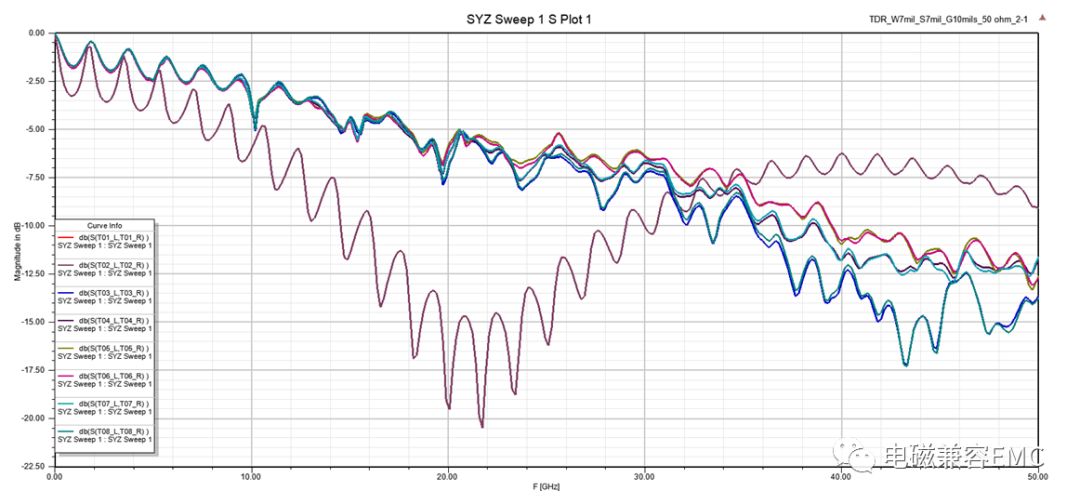
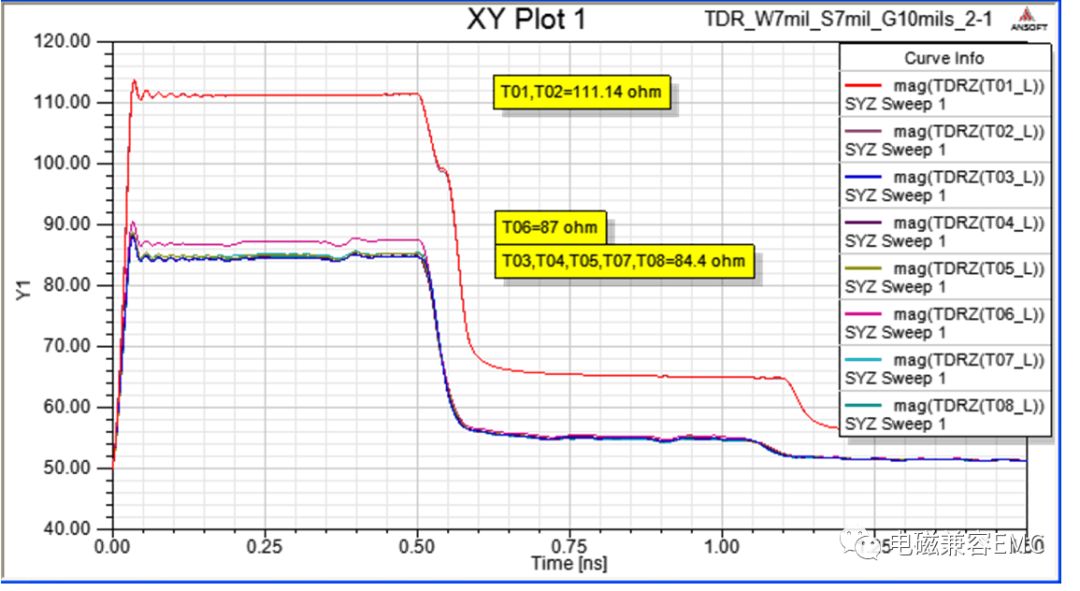
Fig28.TDR results

T03~T08是一樣的結構，S21應該都差不多，從此例的模擬結果來看，SIwave的精度大概到25GHz，而Ansoft當時給出的官方說法是SIwave適用于DC~50GHz。

5.1.2四條線穿插一條地線

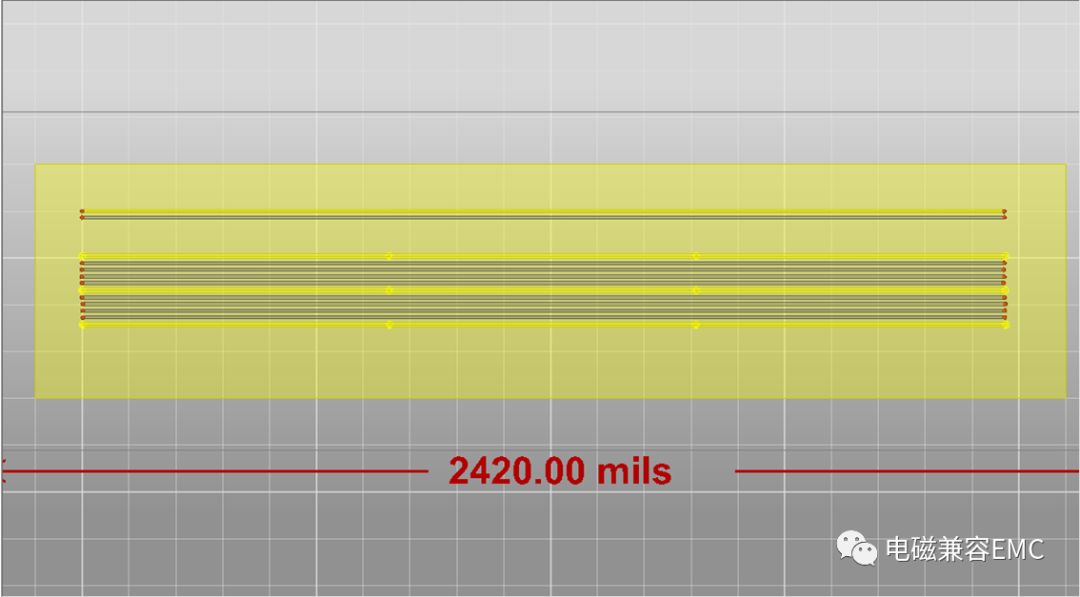
Fig29.四條線穿插一條地線

Fig30.S-parameters for S21

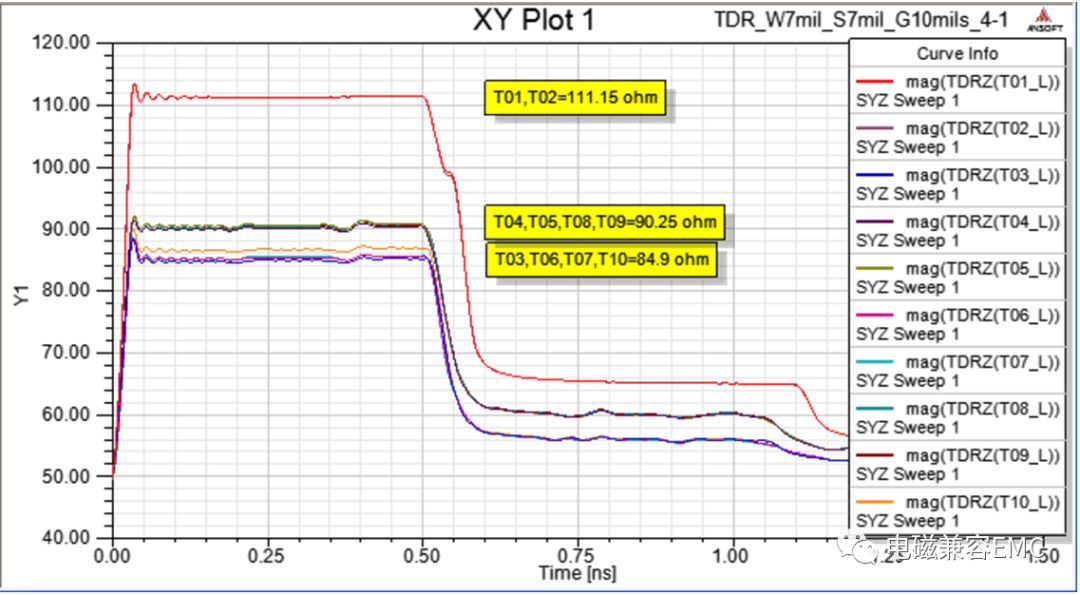
Fig31.TDR results

只要有伴隨地線，不管是兩條線穿插一條地線，或是四條線穿插一條地線，S21在20GHz以內表現都差不多（1dB）。但如果沒有伴隨地線，在1GHz就可以看出差異，S參數特性差很多。

沒有伴隨地線的信號，特征阻抗明顯大很多（T01，T02=111Ω），而只要有伴隨地線，不管是兩條線穿插一條地線，或是四條線穿插一條地線，特征阻抗會在84~90Ω之間。這里的地線為10mil，并不是很寬，via間距為17mm。

5.2 防護地線線寬的影響

如下圖所示，建立特征阻抗為50Ω的微帶線模型，線寬為14mil，介質厚度8mil，介電常數4.4，走線長度為1975mil，兩根信號線間有一根可變寬度的伴隨地線，地線通過兩端接地。查看隨地線寬度的變化，受擾線上噪聲波形的變化情況。伴隨地線初始寬度為5mil，每次增加寬度為2mil。

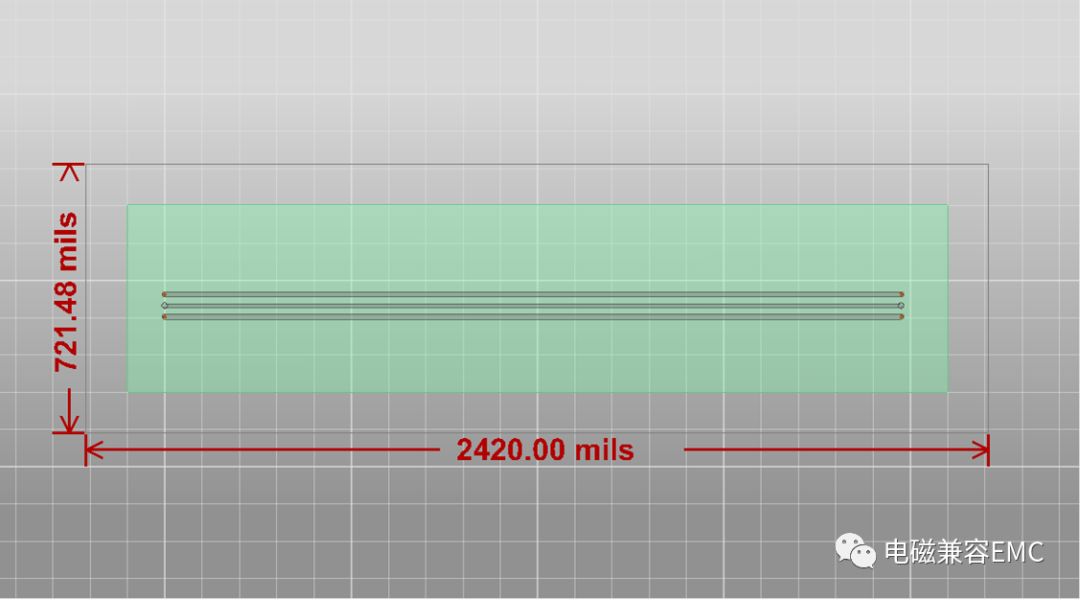
Fig32.兩根走線間的伴隨地線

6、防護過孔對串擾的影響

PCB中過孔的設計是多數人容易忽略的環節，過孔的設計直接影響到諸多參數，對于電源平面過孔，會直接影響到電源網絡的壓降，分布參數，改變電源網絡諧振特性；對于信號部分，過孔的引入會對信號的完整性造成影響；當用作板上各層GND間的連接時，過孔直接影響GND平面噪聲電流的分布，關系到信號回路面積的大小。

盧俊郎等在《The Via'sEffects on PCB Traces》一文中對于過孔效應的分析中提到以下幾點：

對于同一過孔而言，數學過孔模型比實際過孔測量的電容效應大，且過孔的電容效應與電感效應相比，以電容效應為主。

走線上第一個過孔對阻抗不連續的影響最大，隨著過孔數的增加，過孔電容效應增加不明顯。這是因為過孔與傳輸線會帶來高頻信號損耗，所以分析儀器所測量到的效應也遞減。

厚度越薄的PCB，過孔電容效應越小（電感效應也會越小）。

過孔的電容效應，對微帶線與帶狀線的影響差別不大。

線寬大于或等于過孔直徑時，過孔所形成的阻抗不連續性幾乎消失，此時的過孔效應很小。

以過孔換層走不同層時，若是能參考同一地平面，過孔的電容效應較小（電感效應也會越小），換層所引起的阻抗不連續性較輕。

李麗平等在《防護線減小微帶線間串擾的FDTD分析》一文中提出，只要：（1）添加有接地過孔的防護線并使過孔間距小于信號在Tr/2（Tr：傳輸信號的上升時間）時段內的傳輸距離；（2）在滿足線間距布線規則的前提下，將防護線適當加寬而又維持三條線（防護線和兩條微帶線）中兩兩之間的中心距不變，就能有效減小線間的遠端和近端串擾。

按照5.2節模型，在中間防護GND走線上每隔250mil放置一個GND過孔，如下圖所示。

Fig33.帶有GND孔的防護地線

采用SI9000計算得到單線阻抗為144.22Ω，因為伴隨GND的緣故，實際用siwave計算得到TDR阻抗為110.19Ω。該走線時延為140.247ps/in。為滿足孔間距小于Tr/2，RT須大于70ps。

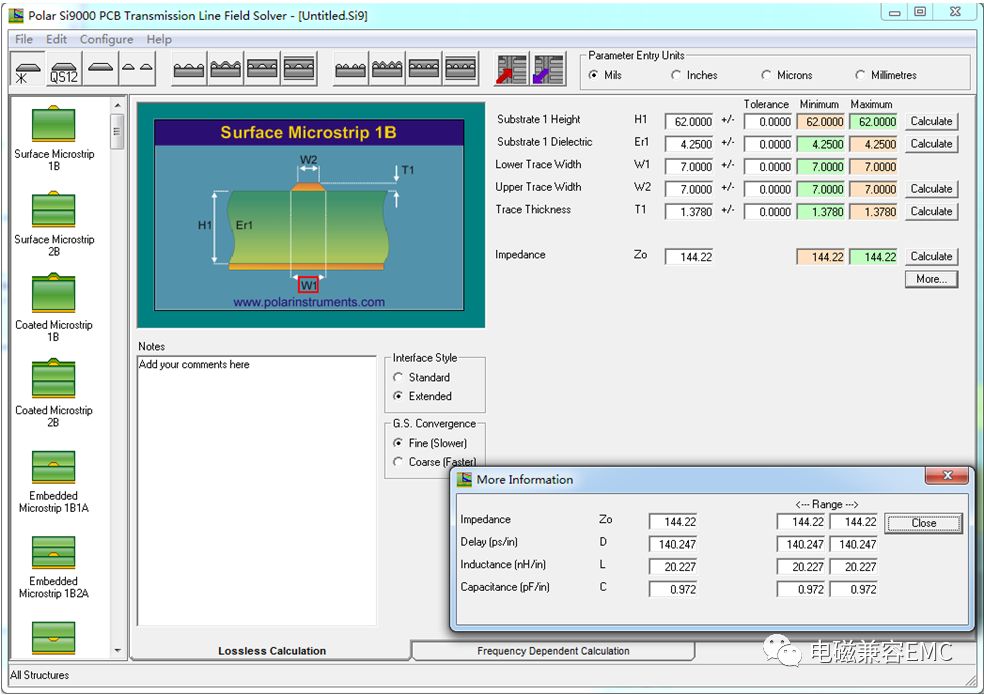
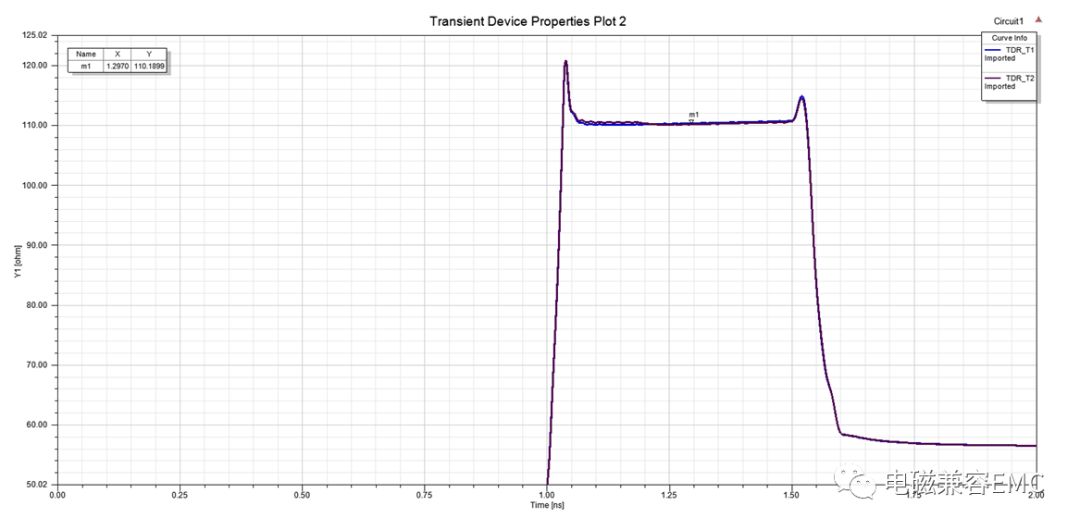
Fig34.走線特征阻抗與時延

我們將RT時間分別設置為40ps、70ps、100ps，查看victim line上串擾電壓幅值的變化，如下圖所示。可以看出，上升沿時間的變化，對于近端串擾電平的影響不大，主要影響遠端串擾電平。Tr/2大于孔間距的定義是處于對遠端串擾防護的設計要求。當Tr時間不變，改變過孔間距的情況會得出相同的結論，感興趣的讀者可以自己去計算一下。

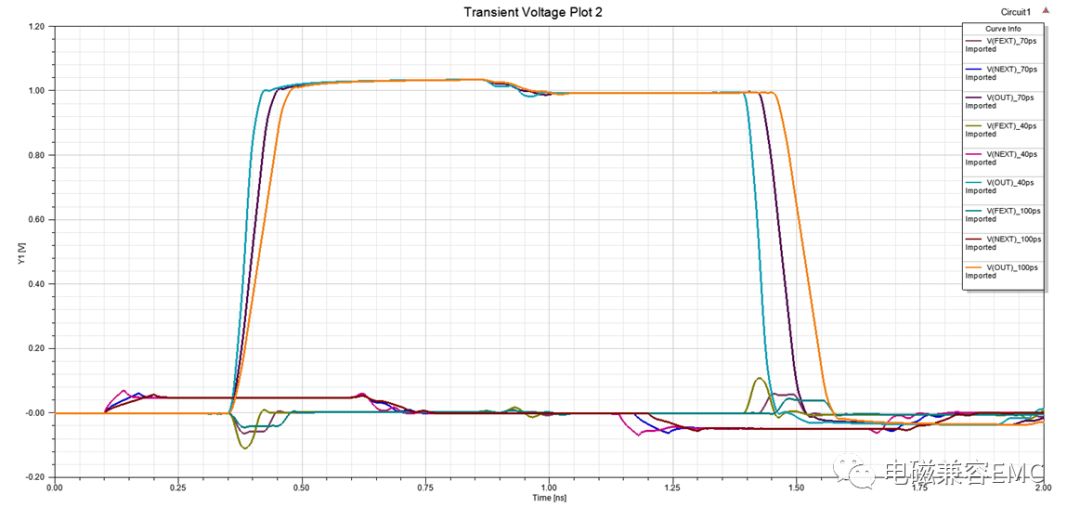
Fig35.不同Tr下的串擾電壓波形

注意：高速信號過孔間也會存在串擾，對于板厚較厚的PCB來說，以3mm單板為例，一個通孔在PCB板厚方向上的長度可以達到將近118mil。如果PCB上扇出過孔間距較小，如BGA封裝的IC，其扇出過孔間距只有幾十mil。這時，過孔間垂直方向并行距離大于水平方向間距，就需要考慮高速信號過空間串擾問題。高速PCB設計時應該盡可能最小化過孔根長度，以減小對信號的影響。對此感興趣的讀者可以去TI論壇中查看《高速差分過孔之間的串擾分析》一文。

7、Minimizationof Crosstalk

7.1吳瑞北的設計方法

在Crosstalk_App一文中列舉了降低串擾的集中設計方法，分別如下

? 在布線允許的前提下，盡可能增加S，降低H；

? 關鍵的信號線，如系統時鐘，采用差分布線；

? 在有顯著耦合的層間使用正交布線；

? 如果條件允許，盡可能采用帶狀線而不是微帶線；

? 信號線間并行長度控制在最小；

? 在PCB板上減小元件間走線的擁擠；

? Use slower edge rates with caution.

? Use genius layout design, say Tx-line interpose.

7.2 Y.-S. Cheng, W.-D. Guo等的觀點

他們在“Enhancedmicrostrip guard trace for ringing noise suppression using a dielectricsuperstrate”一文中提出，通過調整阻焊層厚度和介電常數，可以達到抑制串擾的效果。參考圖6中遠端串擾幅值的公式，可以發現，當阻焊層介電常數與厚度為某一特定值時，遠端串擾將會消失。

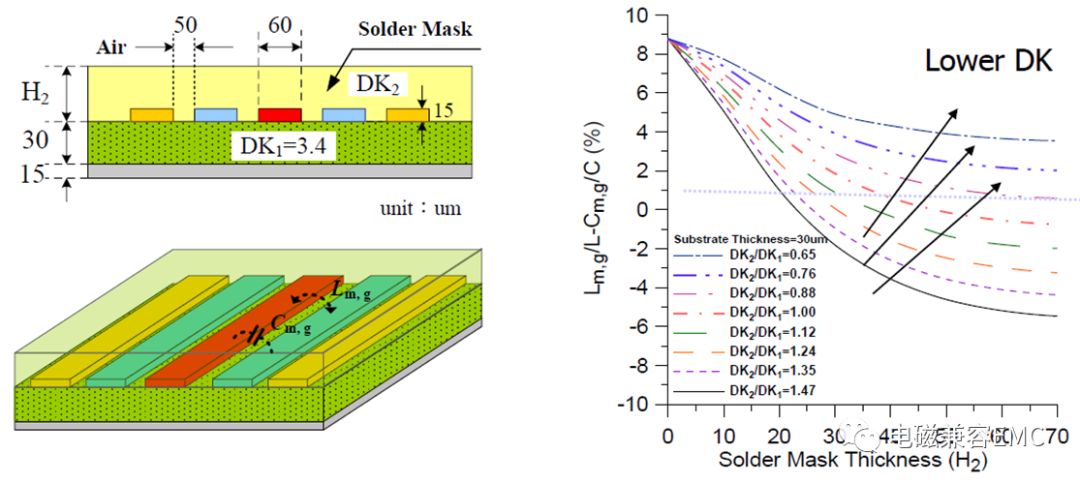
Fig36.Novel Guard Trace Design

8、ANSYS串擾檢查模塊

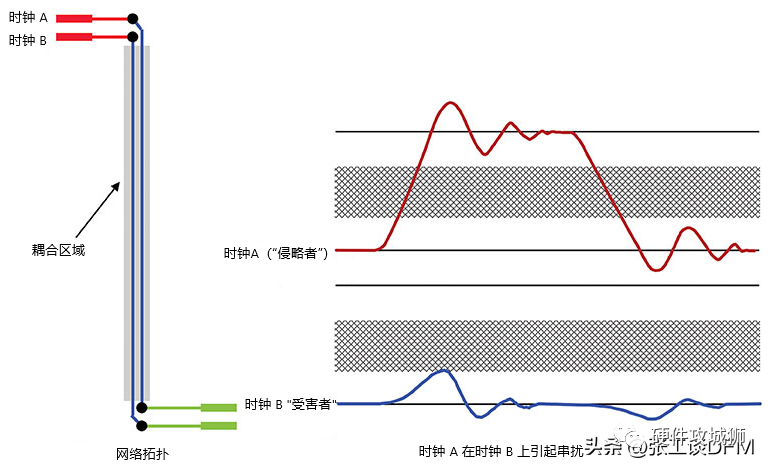
ANSYS SIwave中提供了CrosstalkScan串擾分析模塊，分別有時域和頻域選項，可對單線/差分線進行串擾的快速分析，圖33中以某PCB為例，圖中箭頭位置為U1的晶振X2，時鐘走線XTALIN與信號線A_HSYNC_DAC1有一段較長距離的平行走線，需要評估時鐘走線對信號線的影響。

Fig37.SIwave仿真某PCB示例

8.1 參數設置

查看芯片手冊和原理圖，可以得知A_HSYNC_DAC1信號為RGB輸出信號，電平為1.8V，速率為400MHz，XTALIN信號電平同樣為1.8V，速率為27MHz。查規格書中DAC信號上升時間為0.58ns~1.7ns取1ns，DAC信號為查分形式，差分阻抗為75R，對地阻抗為37.5R。XTALIN信號上升時間在15pF負載下為4ns，這里為12pF，將其設置為3ns。

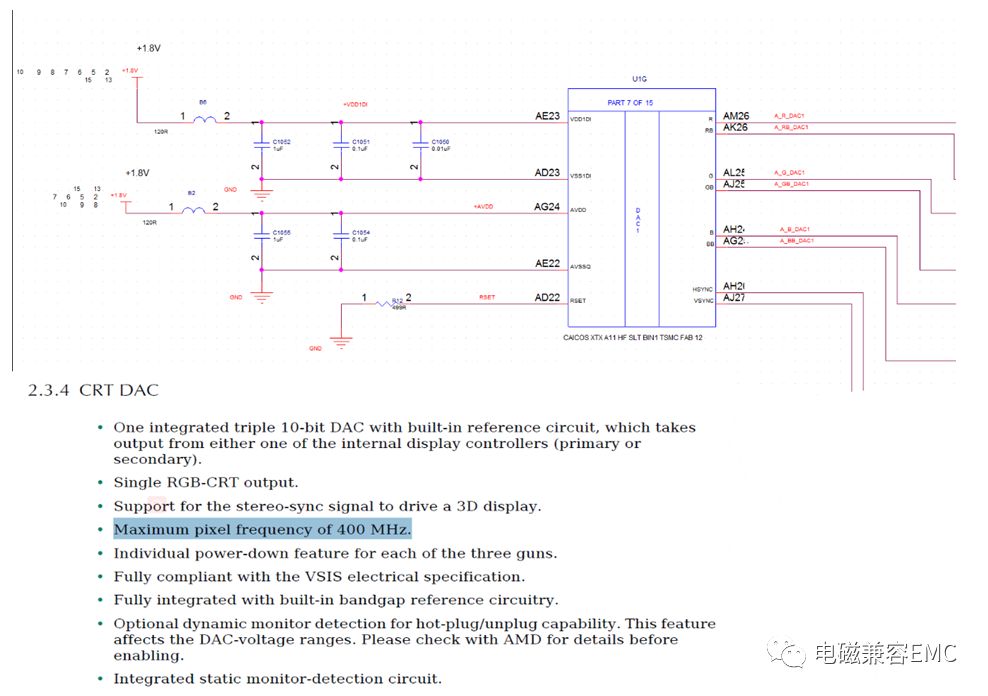
Fig38.信號參數

進行仿真前，將精度調制合適水平，crosstalk收斂精度調整為-60db，求解頻率調高到20GHz，然后選擇Time domain時域仿真，將信號對應的參數填入兩根走線的信號定義中，選擇launch開始仿真。

Fig39.參數設置

不到半分鐘后仿真結束，查看FEXTt和NEXT端各自耦合到的電壓波形，如下圖所示，從結果可知，A_HSYNC_DAC1在XTALIN線上產生的NEXT耦合噪聲最高，約為0.001V。一般信號走線中串擾電平的安全閾值約為信號電平的5%，因此這兩根走線在布線上認為是OK的。

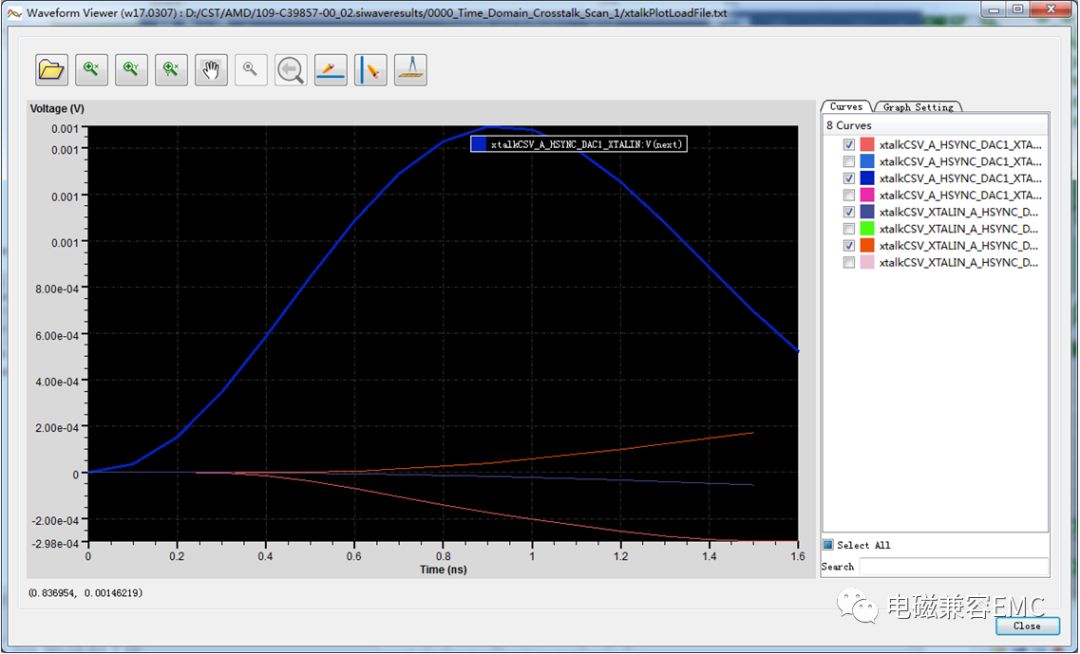
Fig40.crosstalkresult

結果中不僅提供了信號線上耦合的波形，而且有峰值柱形圖及FEXT/NEXT時域耦合峰值位置，從耦合結構圖中可以直觀的看到走線中耦合較嚴重的部位。從下圖中可以看出，平行走線中局部耦合較為嚴重，當結果超過安全閾值時，就需要對其進行處理。

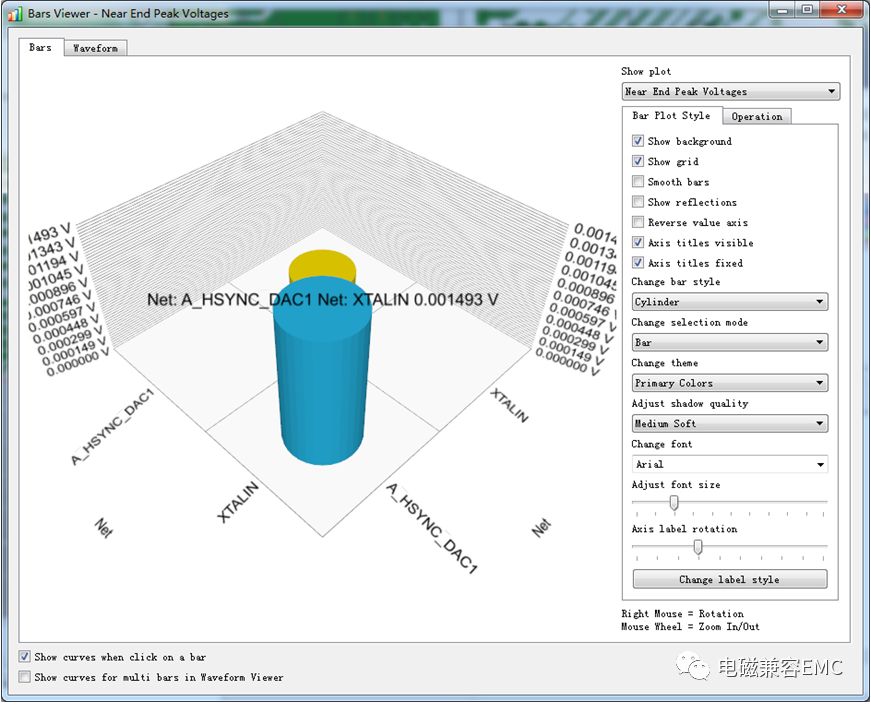
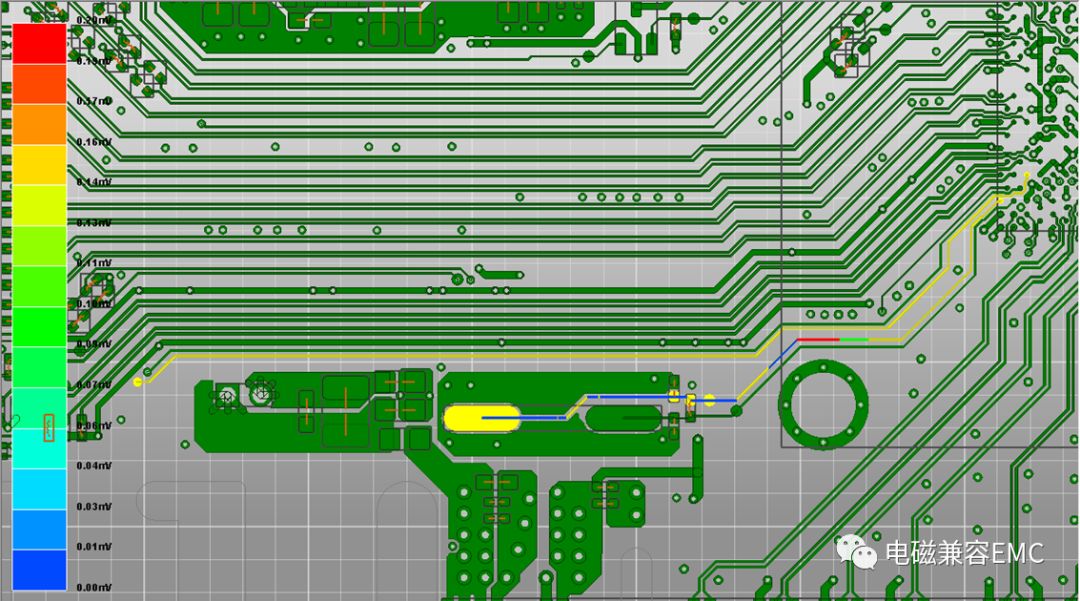
Fig41.Peak Voltage and Time Domain Crosstalk Max Voltages results

因為走線整體布局已經確定，這里選擇在線間加部分伴隨GND走線，當優化后再次進行仿真后，可以看出，原先位置的電平已經降下來了。

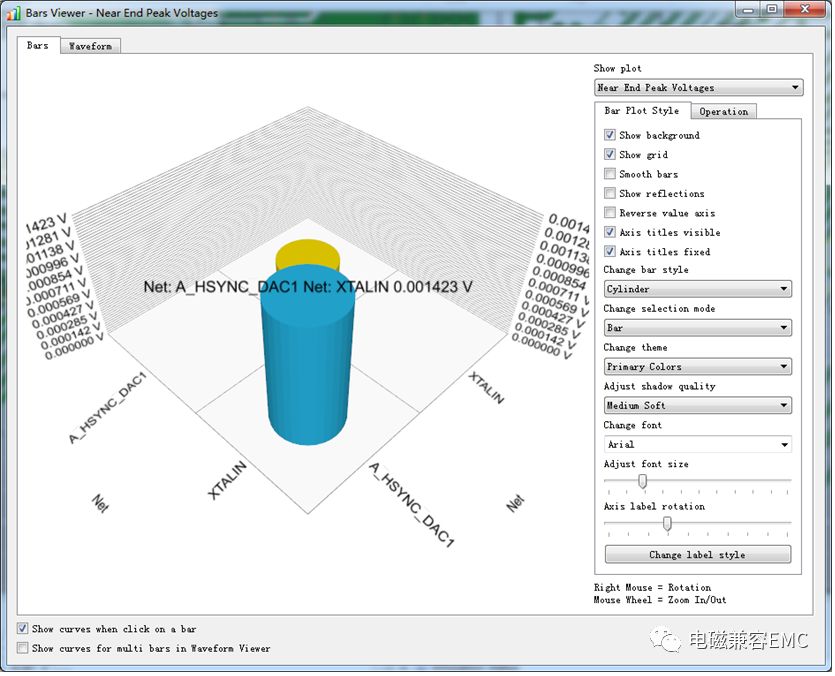
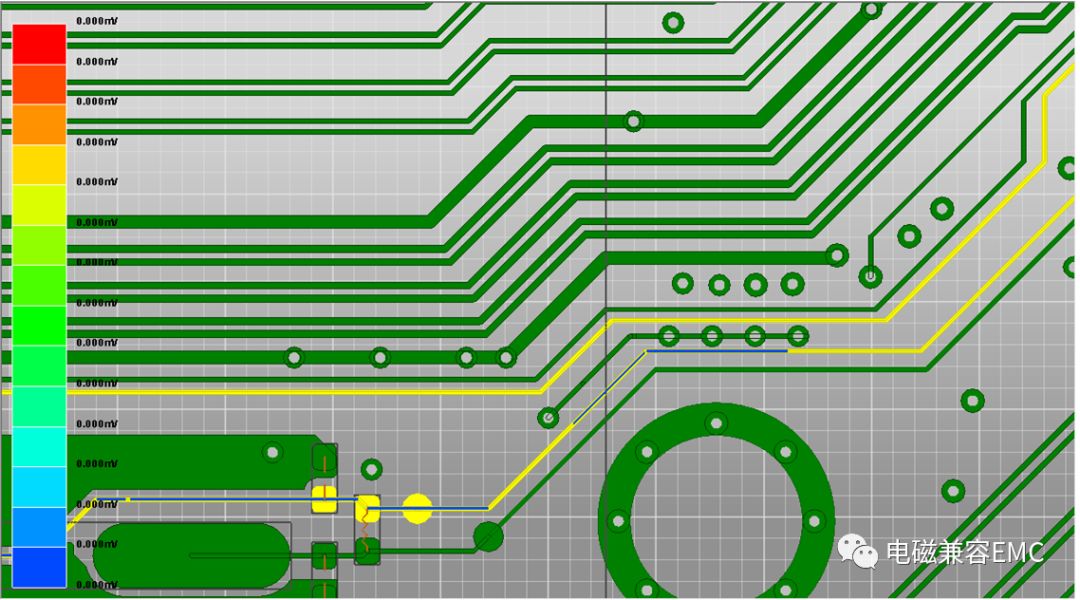
Fig42.Peak Voltage and Time Domain Crosstalk Max Voltages results

8.2 優化

采用S參數模型仿真時域串擾，因為Time Domain Crosstalk功能并非基于精確的S參數求解，所以為了清晰的認識優化前后的對比，這里用S參數模型，在circuit design內創建串擾電路模型。優化前后的串擾波形如下圖所示（_2為初始，_1為優化后）。可以看出，優化后正向電壓增加，負向電壓減小，整體平緩，但是優化后并未有較為明顯的變化，是否可以認為防護線沒有作用呢？

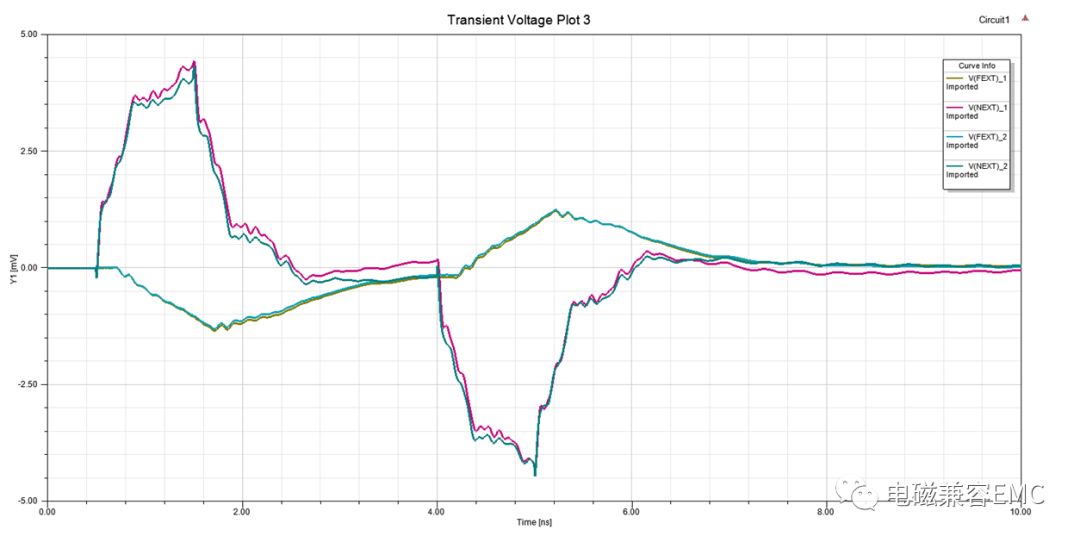
Fig43.Results of crosstalk

注意：這里對比不明顯的原因在于，第六章中提到防護地孔與信號上升沿之間的關系，實際電路中信號Tr是不變的，多數情況下也不允許添加電容增加Tr時間，對于這種情況，只能盡可能保證線間距大于3W。

9、線纜間的串擾

線纜的設計在EMC設計中，常常會忽略線纜間的串擾。然而實際情況是，有相當一部分產品的設計缺陷來自于線纜間的串擾，這類問題多來自軍品、醫療、汽車等標準規范要求嚴格，結構復雜，存在諸多互連線纜的產品上。

相鄰導線間的串擾既可以是由互電容產生的電場耦合引起的，也可以是由互電感產生的磁場耦合引起的，第三種形式的耦合是通過共阻抗引起的。

當遇到線纜接口數據傳輸錯誤的情況，未必一定是串擾造成的，還有一種可能是由于線路與負載阻抗不匹配而產生的反射，后者往往會被誤認為是串擾。（關于反射下文會詳細的進行總結）

那么，當EMI問題出現，該如何確定是否為串擾引起的呢？一種實用方法是把干擾源和敏感導線分開。若這種方法不易實施，那么將干擾源信號上升沿降低或將頻率降低，則可能是另一種可行的方法。在產生間歇性EMI并懷疑是串擾引起的情況下，可以用增加干擾源信號的幅度、頻率、速率或通過變壓器或電容器注入另外的噪聲源的方法來加以證實。此時，若EMI趨勢是增加的，則可能已經發現有串擾源存在。

當串擾已經發生在PCB線路間，相鄰導線時，首先需要確定耦合主要是電場耦合（容性），還是磁場耦合（感性），因為不同的耦合方式決定了不同的處理手段。大衛.A.韋斯頓在《電磁兼容原理與應用》中提出一種簡單有效的方法。作者將干擾源和敏感電路之間的特性阻抗和敏感電路與地線之間的阻抗用在串擾預估中，該準則如下：

當干擾源和敏感電路阻抗乘積小于3002Ω，則主要是磁場耦合；

當阻抗乘積大于10002Ω時，則主要是電場耦合；

當阻抗乘積在3002Ω和10002Ω之間，則磁場或電場耦合能否起主要作用，要取決于電路的幾何尺寸和頻率。

看到這里，細心的讀者不難發現，磁場耦合或是電場耦合分別發生在特定電路中。產品中電源部分往往是低阻的（磁場耦合），信號往往是高阻的（電場耦合），而電源與信號之間的耦合介于兩者之間。

對于直徑為d，距離接地面高度為h的單線，如下圖所示：

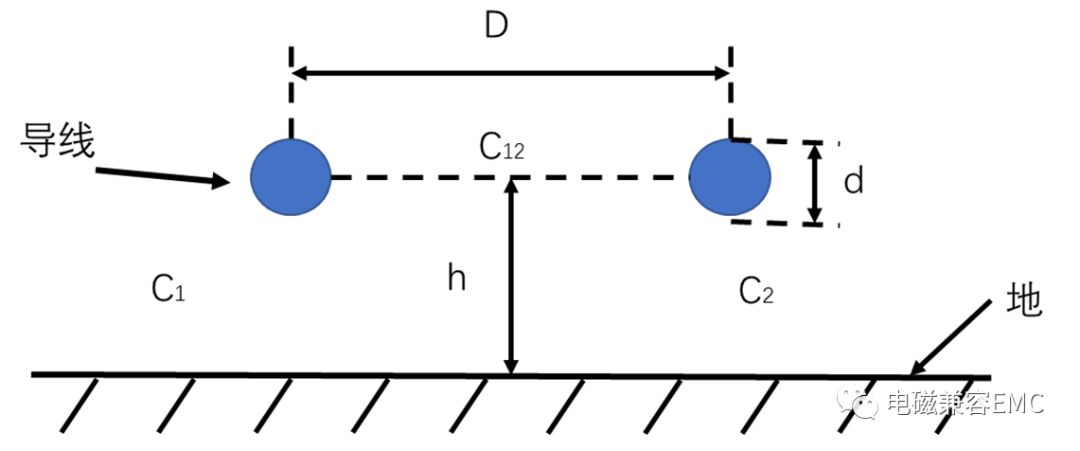
Fig44.Cable model

其導線電感L（Uh/ft）為：

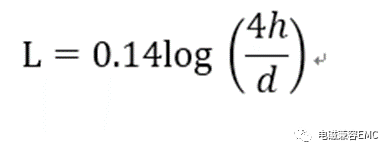
兩根導線之間的互電感M（Uh/ft）為：

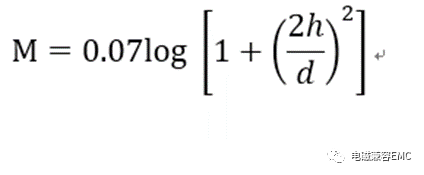
線對地電容為：

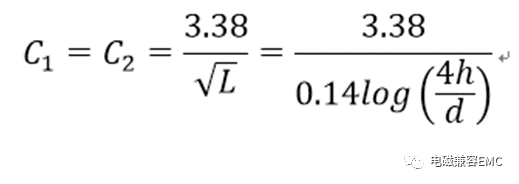
線對線電容（互電容）為：

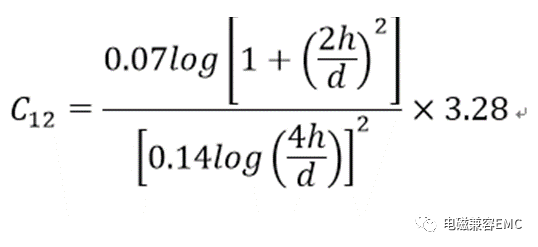
平行雙線間串擾模型如下圖所示：

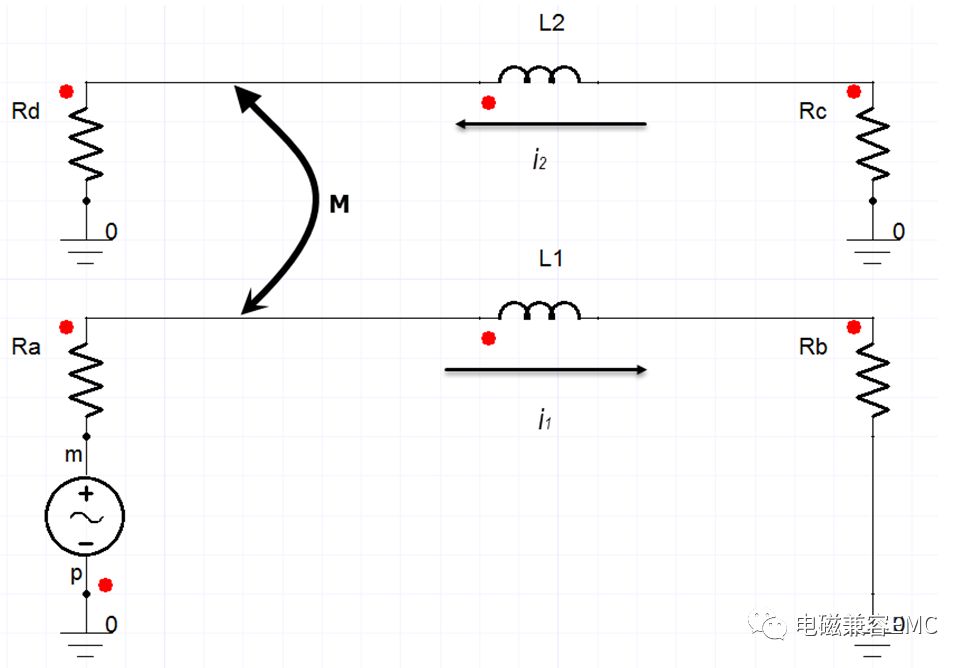
Fig45. Cable 耦合模型

受干擾負載Rd兩端的電壓幅度可由以下公式計算得出：

式中可以看出，當線束與地面距離h下降時，導線電感L和線間的互感M同時下降，當h降低到之前的1/10時，自感L降低0.14（uH/ft）（按照最大距離h為50mm，d為2mm計算，一般情況下產品內部線束的自感約為0.2（uH/ft）左右），互感降低的趨勢隨h與間距D的比值變化而不同。從Vd的計算公式中可以看出，當受擾線為高阻，或者騷擾線為低阻時，串擾增加。下面采用CST cable studio工具將這種變化描述給讀者。

9.1、單線間的串擾

9.1.1建立線纜模型

選擇0.2mm線徑的單線，長度為100mm，線間距5mm，線與GND間距5mm，driver line的信號Tr為0.1ns，Tf為0.1ns，周期2ns，50%占空比，幅值1V。

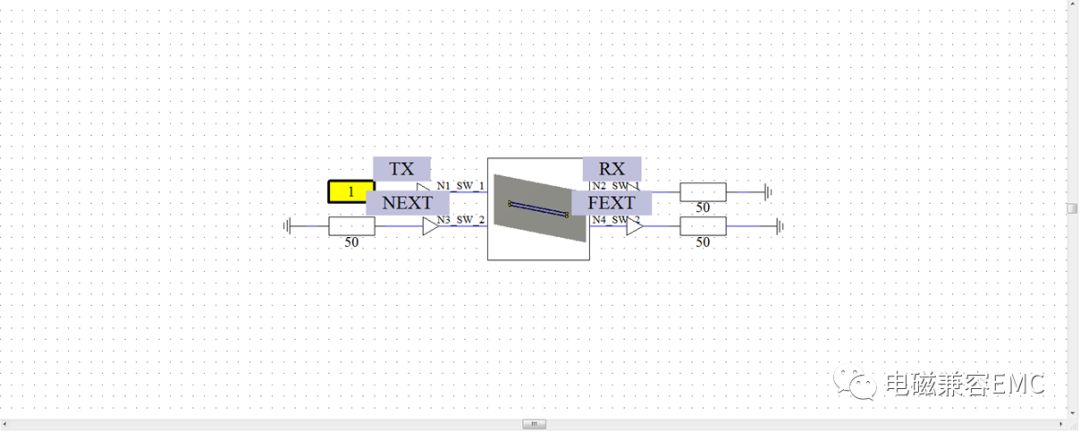
Fig46.耦合線模型

查看victim line上近端和遠端波形，如下圖所示，受擾線上電壓幅值約為施擾線電平的2%。即使施擾線信號電平增加到3.3V或者5V（多數信號電平），受擾線上噪聲電平也是可以接受的。

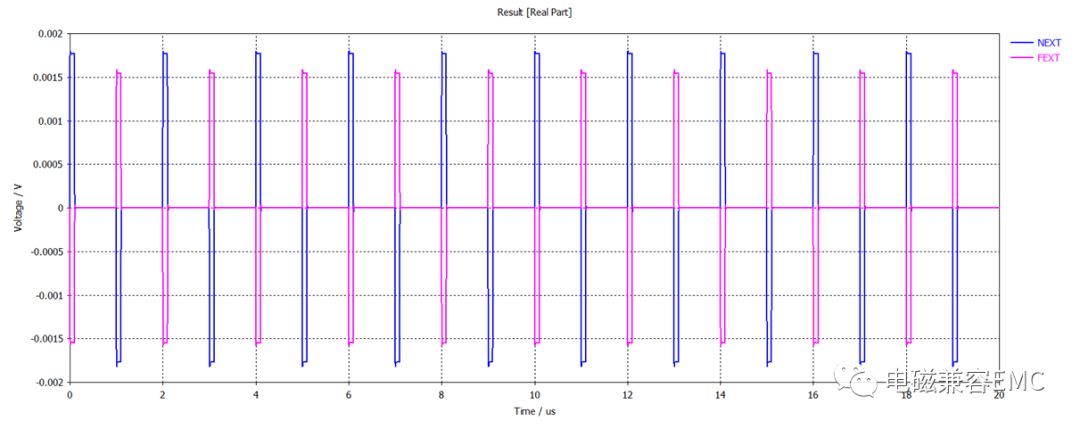
Fig47.受擾線噪聲電壓波形（接地阻抗50R）

9.1.2線束設計是否一定滿足需求？

那么，實際中這樣的線束設計是否一定滿足需求呢？答案是否定的，因為實際電路中信號線阻抗往往是高阻的，尤其是采樣信號線束的阻抗通常在千Ω以上，當受擾線阻抗增加到1MΩ時，線上噪聲電平將增加到不能接受的水平。如下圖結果中，FEXT，和NEXT電平增加到0.18V，現實產品中往往將線束扎起來（D減小），并且有較長的走線（如EMC測試要求線束長度為2米左右）。這些情況都會增加受擾線上噪聲電平，尤其是在做EMS抗擾度測試時，若信號線不做濾波等防護處理，產品是極易被干擾的。對比上下兩圖，可以看出FEXT與NEXT由開始的反相變為同相，這是為何？這個問題留給讀者去思考。

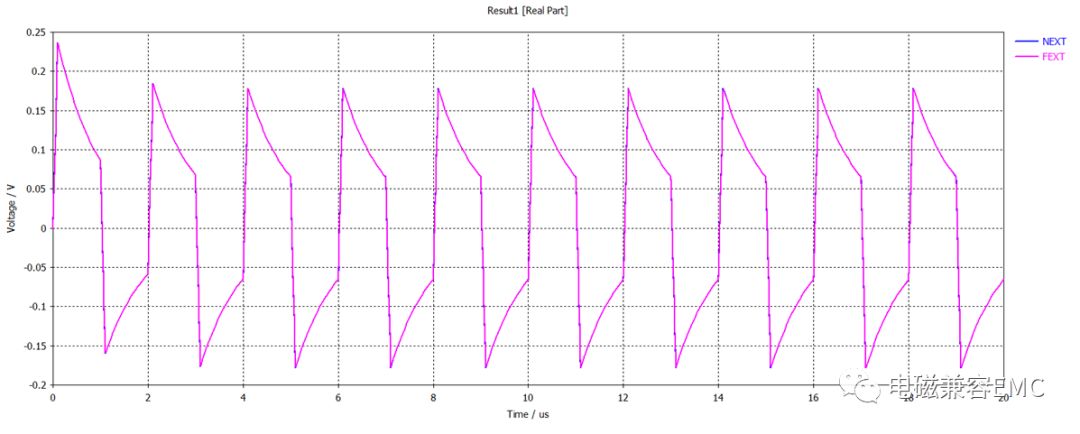
Fig48.受擾線噪聲電壓波形（接地阻抗1MR）

當信號線整體阻抗變化時，其噪聲電平與信號線阻抗間的關系如下圖所示。可以看出，將信號線阻抗控制在較小水平，可以有效降低串擾電平幅值。從中也可看出，在信號線上采用電容去偶的效果是最好的，遠優于電感（原因在濾波篇中會講到）。

Fg49.受擾線噪聲電平隨接地阻抗變化

9.1.3 線纜中的“3W原則”

實際上人們在產品設計中往往只關注PCB中上信號走線，忽略線束設計。線束實際上是PCB的延伸，同樣需要在布局上重視。當增加線束間距D，觀察串擾幅值的變化，如下圖所示，當間距D增加到15mm時（3倍h），噪聲電平下降趨于平緩。因此，對于敏感信號，需要嚴格控制線束的走線，必要時需采用獨立走線的方式。

注：改變導線與GND間距h，得出的趨勢一致。

Fig50.受擾線噪聲電平隨線間距變化

9.1.4 GNS距離的影響分析

前面公式中可以看到，降低線束與GND平面的距離，可以降低線束間串擾的幅值。這里采用軟件計算出隨GND間距h變化，串擾幅值變化的情況。從下圖結果中可以看出，隨著線束與GND間距增加，串擾幅值增加，在設計允許的間距范圍內，整個趨勢近似為線性增加。也就是說，當h減小一倍，受擾線上噪聲電平幅值便降低3dB。

注：改變導線間距，得出的趨勢一致。

Fig51.受擾線噪聲電平隨GND間距變化

9.2 不同規格線束間的串擾

多數產品設計中往往采用了不同種規格的線束，既有單線，也有雙絞線，同軸線，屏蔽雙絞線，甚至多線束屏蔽線等等。那么，這些線束對串擾的防護能力分別如何呢？下面就對這個問題進行分析。

采用CST cable studio分別建立單線，雙絞線，同軸線和屏蔽雙絞線模型，如下圖所示。

Fig52.仿真線束截面圖

線束長度同樣設置為100mm，線束間距為5mm，距離GND平面5mm。線束排列為，最下方施擾線（單線），向上每隔5mm以此是單線、雙絞線、同軸線、屏蔽雙絞線。提取S參數后的模型如下圖所示。

注意：這里雙絞線指的是差分雙絞。

Fig53.線束拓撲圖

仿真完成后，查看各線束上噪聲電壓幅值，選擇FEXT結果，可以看到相鄰線束上噪聲電壓波形分別如下（數值差距太大，分別進行對比），可以看出，單線和雙絞線上的串擾噪聲遠高于同軸線和屏蔽雙絞線，而雙絞線上噪聲電平最高。多數工程師在產品設計中將線束雙絞，這里可以看出雙絞做法未必總是有利的，它并不會降低線束上的共模噪聲，反而會增加噪聲幅值。由互易定理可知，易耦合噪聲的線束反過來也容易干擾其它線束，所以對于那些由于設計需要不得不雙絞的線束（如非屏蔽網線，視頻線，CAN線等），需要與其它線束保持距離（或者直接屏蔽），具體間距可以參考9.1節的結果。

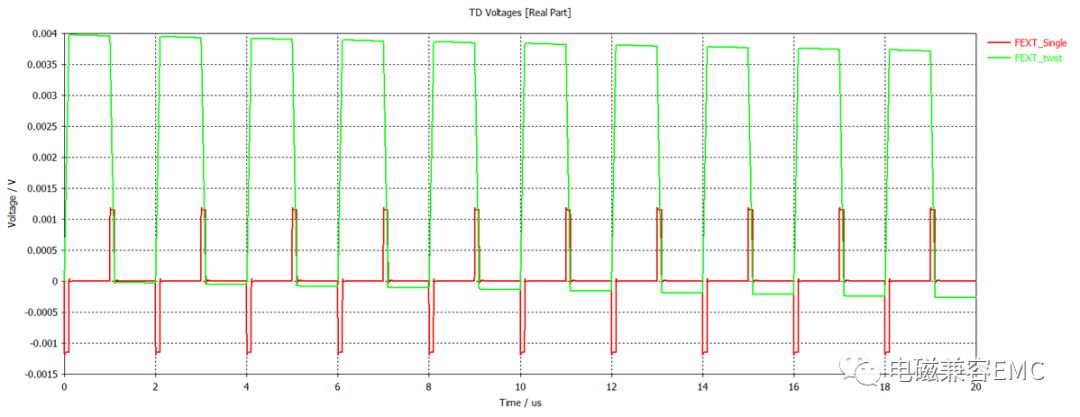
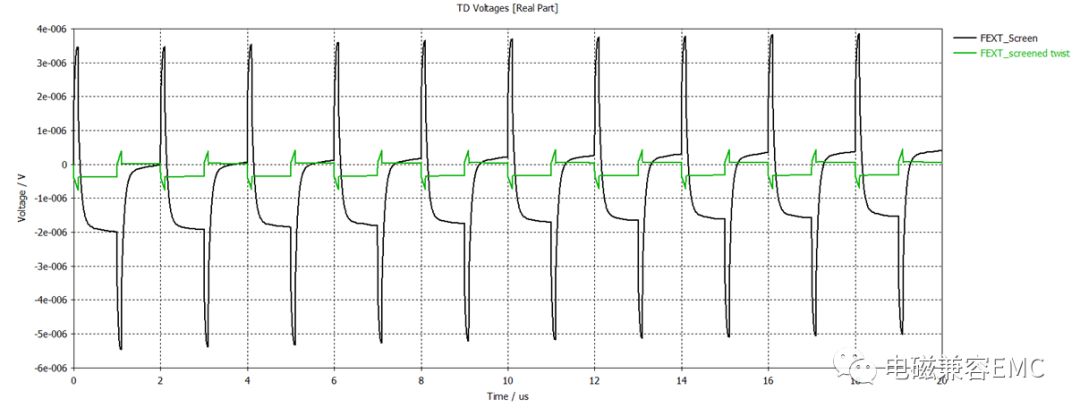
Fig54.不同線束上遠端串擾電壓波形

實際中當網線，視頻線，CAN線等差分線中工作信號為差模，所以我們需要對差模信號上的串擾進行評估，而非共模。當改變測試探頭后，我們可以看到，雙絞線上差模噪聲幅值是異常小的，小到只能單獨拿出來查看。

注意：上圖中的雙絞屏蔽線結果為共模噪聲，若是換為差模噪聲，其幅值將會是最小的。

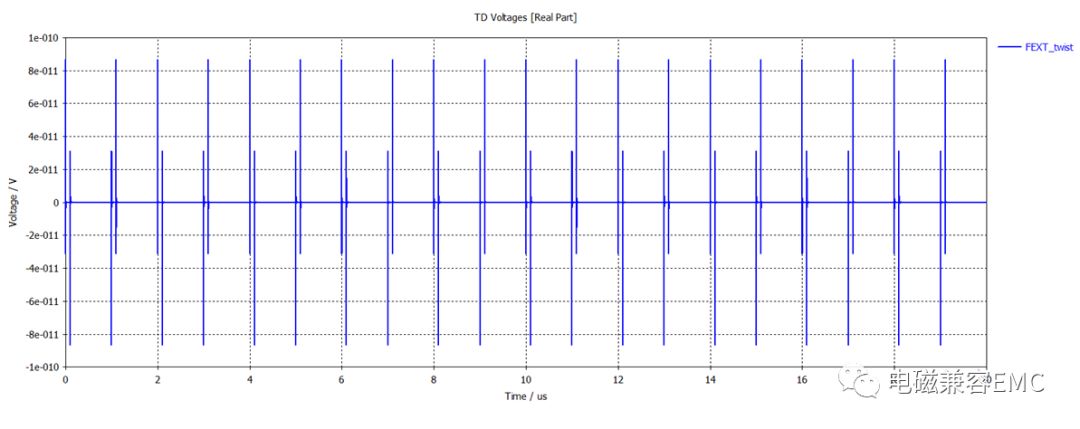
Fig55.雙絞屏蔽線差模噪聲電壓波形

那么，對于那些將單線雙絞起來的做法，是否會有差異呢，下圖結果中可以直觀的發現，將單線雙絞后，噪聲電平較未做雙絞情況下降低了約30倍（假設單線輸入阻抗都為10kΩ）。

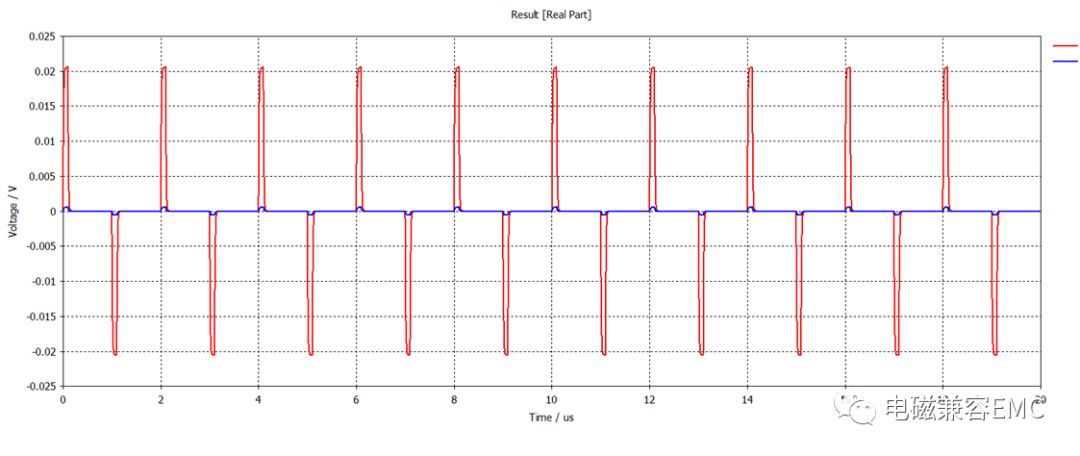
Fig56.單線雙絞前后近端串擾噪聲電壓波形變化

9.3、同一線束中的不同規格線纜間的串擾

實際產品設計中，我們會遇到各種類型的線束，如CAT5E_STP（超五類屏蔽線），CAT5E_UTP（超五類非屏蔽線），USBr3（USB3.0高速數據線）等等，并且線束廠家會滿足客戶對于線束設計的要求。那么，如此多種類的線束應該如何去設計呢？下圖最后一張為自定義線束，與9.2節相同，一根大的屏蔽線束內包含了單線、雙絞、同軸、屏蔽雙絞等常見的線型。

Fig57.不同規格線束橫截面

當在上圖右下角的單線中注入噪聲，我們觀察其它同在一根線纜內的線束上噪聲情況，以此來判斷這條線束是否符合要求。首先我們查看其它線束上的共模和雙絞線（差分）上的差模噪聲。可以明顯看出雙絞線上差模噪聲是最高的，單線次之，噪聲最小的是屏蔽雙絞線。

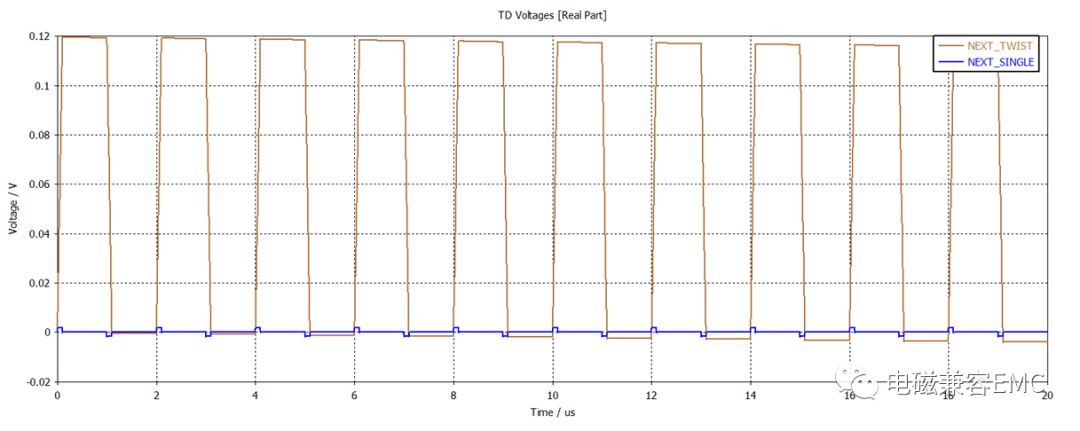
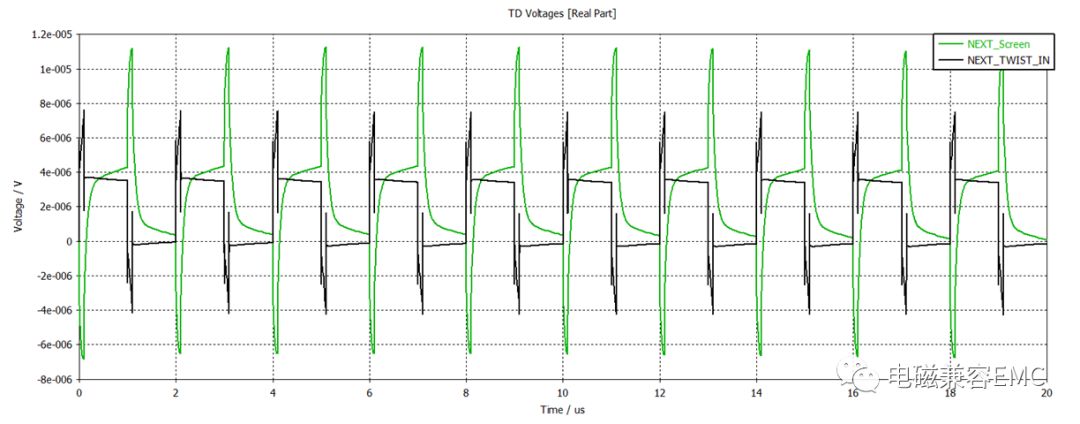
Fig58.線束內不同線間近端串擾電壓波形

當雙絞線為單線而非差分形式，我們關注的噪聲模式轉換為共模，再來查看線束上噪聲情況我們會發現，雙絞單線要比單線上噪聲幅值低一倍還多。而同軸和屏蔽雙絞線似乎沒有什么變化。

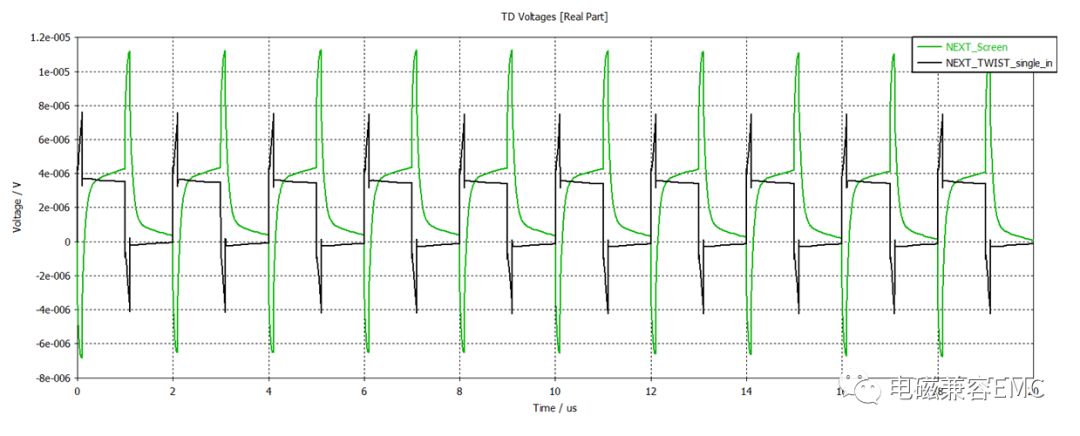
Fig59.單線雙絞后近端噪聲電壓波形

結論：線束設計中的串擾與線束的布局和處理方式相關，條件允許情況下，線束應該盡量單獨屏蔽處理，若產品成本不允許，也可以通過雙絞等方式對線束處理，從而降低串擾可能造成的影響。對于有復雜線束要求的設計，需要慎重考慮線束間的串擾可能造成的影響，這個串擾既有可能存在于同一線束內，也可能存在于不同線束間。