引言
1998 年,Huang 等人提出了一種新的信號處理方法:經驗模態分解方法(Empirical Mode Decomposition,EMD)。它用不同特征尺度的數據序列本征模函數(Intrinsic Mode Function,IMF)分量來逐級分解信號。
該方法可以對一個非平穩信號進行平穩化處理。
在EMD分解中,每個IMF需要多次“篩選”過程,而每一次篩選過程,需要根據上、下包絡計算出信號的局部平均值。上(下)包絡是由信號的局部極大(小)值通過3次樣條插值得到的。但信號的端點不可能同時處于極大值或極小值,因此上、下包絡在數據序列兩端會發散,且這種發散會隨著運算的進行而逐漸向內,從而使得整個數據序列受到影響,這就是所謂的EMD 方法的端點效應。
國內外很多研究者對改進EMD端點效應問題進行了研究。目前,常用的EMD 端點效應處理方法有鏡像法、極值延拓法、神經網絡預測、多項式外延方法、平行延拓法、邊界局部特征尺度延拓法。神經網絡延拓算法的運算速度慢,在工程應用中實時性差。所以本文只對鏡像法、極值延拓法、多項式法、平行延拓法和邊界局部特征尺度延拓法進行比較,從而得到對工程應用有指導意義的結果。
1 EMD方法
EMD方法中假設:
(1)任何信號都可以分解為若干個IMF分量;
(2)各個IMF分量可以是線性的或非線性的,局部的零點數和極值點數相同,且上下包絡關于時間軸局部對稱;
(3)一個信號可包含若干個IMF分量。
每個IMF分量的計算步驟為:
首先,計算原信號x(t) 的極值點,然后用三次樣條函數擬合出極大(小)值包絡線e+(t)( e-(t))。原信號的均值包絡m1(t) 是上下包絡線的平均值:
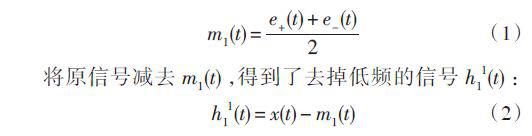
若h11(t) 不滿足IMF 定義的條件,則它不是平穩信號,重復進行上述過程k 次( k 一般小于10),直到找到滿足IMF的定義的h1k (t) ,則x(t) 的一階IMF分量為:
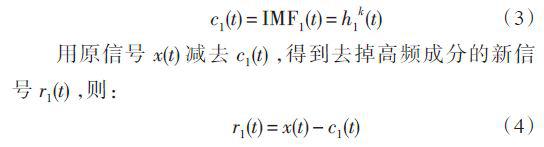
將r1(t) 作為原始數據,再得到第2個IMF分量c2 (t) ,依此類推,得到n 個IMF 分量,直到rn (t) 是單調函數或常量時,EMD分解過程停止。
最后,x(t) 經EMD分解后得到:
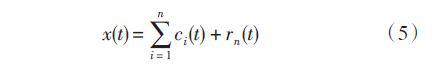
式中rn (t) 為趨勢項,代表信號的平均趨勢或均值。
2 改善端點效應的幾種方法
本文在Matlab下實現了5種常用的改善EMD 端點效應的方法,并用于比較測試,它們分別為:
(1)端點鏡像方法。以信號兩端的邊界為對稱,把信號向外映射,得到原信號的鏡像,形成一個閉合的曲線,從而得到完整的包絡曲線。
(2)極值延拓法。以端點的一個特征波為依據,在兩端各延拓兩個極大值和極小值。
(3)多項式擬合法。對原信號的極值點序列,利用端點處3 個極值點進行多項式擬合計算出的值作為端點處極值點的近似取值,以確定邊界極值點的位置。
(4)平行延拓法。利用端點附近的兩個相鄰極值點(一個極大值,一個極小值)處斜率相等這一特性,人為在兩端定義出兩個極值點。
(5)邊界局部特征尺度延拓法。把調幅趨勢和端點處局部極值點的時間間隔相結合,在信號兩端分別添加一對極大值點和極小值點。
3 端點效應評價指標
本文采用3個指標來評價多種端點效應處理方法的效果:
(1)計算EMD 分解后各分量信號與對應的原信號之間的相似系數ρ 信號的包絡發生形狀畸變,引起端點效應,從而使各個分量的分解不準確。可以比較EMD分解后的各IMF分量和原信號分量之間的相似度,來評價各抑制端點效應算法的抑制效果。
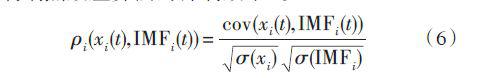
式中:cov-( ) 表示協方差;σ-( ) 表示方差;IMFi 表示信號經過EMD分解后的第i 個模態分量;xi 為相對應的原信號組成分量。ρ 值越大,說明端點效應的抑制越好。
(2)計算EMD 分解后得到的各IMF 分量和原信號相應的分量之間的平均相對誤差[9].
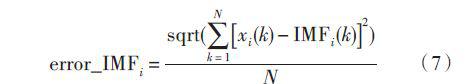
式中:N 表示信號的總個數;xi(k) 表示原信號第i 個分量;IMFi(k) 表示EMD 分解后得到的相應分量。
error_IMFi 越小,說明端點效應的抑制越好。
(3)運算時間。保證算法抑制端點效應效果的前提下,算法不能過于復雜,以滿足實時性。
4 實驗結果分析
假定測試信號是一個調頻調幅非線性仿真信號,其表達式為:
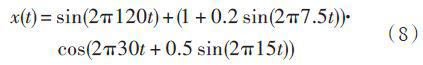
式中采樣頻率1 000 Hz,采樣點數250 點,時域波形如圖1所示。
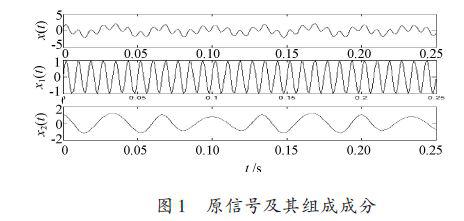
為了比較延拓后的分解結果,將原信號的組成分量一并給出,圖2是沒有進行端點處理的信號EMD分解結果,從圖中可以看到,在兩端點處有比較大的失真,并且會“ 向內污染”.圖2~圖7 中虛線為原分量;實線為EMD的分解結果。
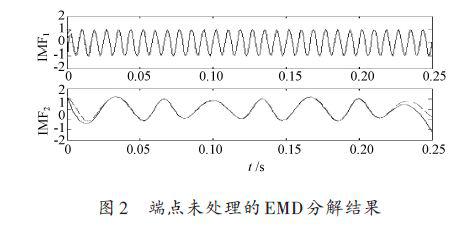
圖3~圖7分別是用端點鏡像方法、多項式擬合法、極值延拓法、平行延拓法和邊界局部特征尺度延拓法延拓后得到的EMD分解結果。
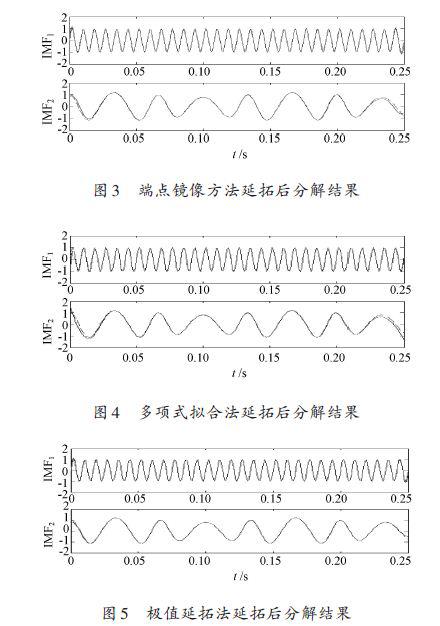
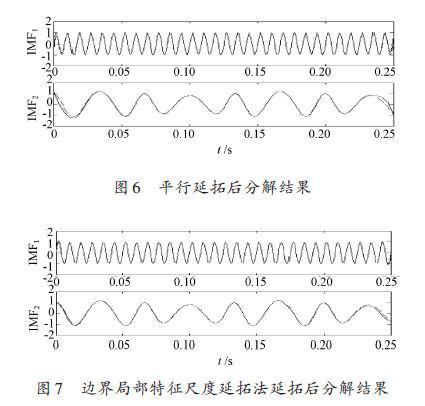
由圖可知,這幾種方法都有效改善了EMD 的端點效應,其中極值延拓法對于端點效應的改善比較明顯,其他方法得到的結果,在兩端仍有發散現象。表1給出了文中所述5種端點抑制方法對所給信號處理后的性能評價結果。
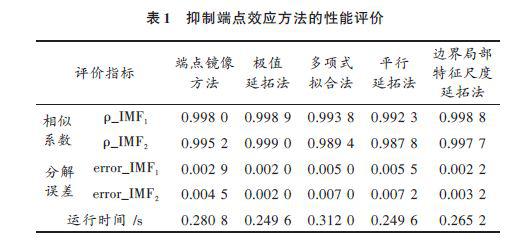
由表1給出參數可看出,對于給定準周期的測試信號,極值延拓法分解得到相似系數最大,分解誤差最小,分解精度最高;平行延拓法得到的相似系數最小,分解誤差最大,分解精度較低。比較運行時間,極值延拓法和平行延拓法計算速度最快,多項式擬合法耗時較長。
5 結語
在EMD 分解過程中,由于多次對局部極大值和局部極小值運用3次樣條插值,從而產生了引起失真的端點效應。對于本文給出的準周期的測試信號,端點鏡像方法、多項式擬合法、極值延拓法、平行延拓法和邊界局部特征尺度延拓法5種方法都能改善EMD分解的端點效應問題。其中,極值延拓法是5種方法中分解效果最好的、運算速度最快的延拓方法,在工程技術應用中處理類似的信號,可以將其作為端點效應處理的主要方法。當然,工程應用中的信號千差萬別,對于不同形式的信號,各種改善EMD 端點效應的延拓方法性能各異。在實際應用中,最好根據所處理信號的特點選擇合適的延拓方法。本文所用評價方法,只對實際工程選用合適的延拓方法提供一個參考。
-
神經網絡
+關注
關注
42文章
4781瀏覽量
101178 -
信號處理
+關注
關注
48文章
1042瀏覽量
103407 -
EMD
+關注
關注
1文章
43瀏覽量
20086
發布評論請先 登錄
相關推薦
Python軸承故障診斷之經驗模態分解EMD原理介紹
基于EMD和自相關分析的輪胎音頻信號處理
emd算法實現
請問能否在LabVIEW平臺下編寫改進后的EMD算法,采集到信號后直接進行分析?
基于EMD的非平穩信號低通濾波技術的研究
空間矢量PWM逆變器死區效應分析與補償方法
基于EMD和自相關分析的輪胎音頻信號處理
基于EMD的語音功率譜分析

改進EEMD電能質量檢測方法(EMD分解信號)
基于語音增強方法的語音端點檢測
EMD信號處理方法如何在LabVIEW和MATLAB中的實現
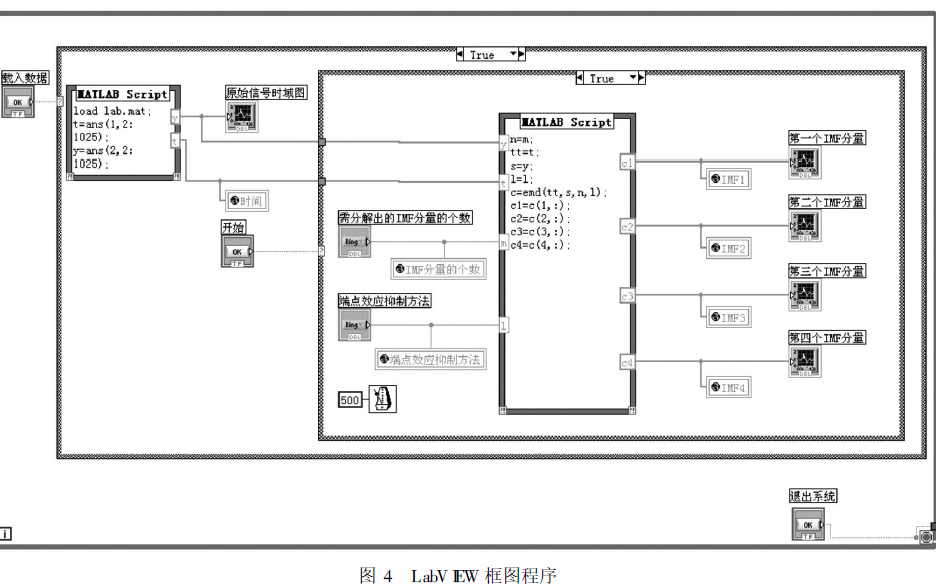




 對五種改善EMD端點效應的方法進行分析
對五種改善EMD端點效應的方法進行分析












評論