在密蘇里科技大學(xué)與百度大數(shù)據(jù)實(shí)驗(yàn)室合作的一篇論文中，研究人員從理論視角對SGD在深度神經(jīng)網(wǎng)絡(luò)訓(xùn)練過程中的行為進(jìn)行了刻畫，揭示了SGD的隨機(jī)項(xiàng)在其選擇最終的全局極小值點(diǎn)的關(guān)鍵性作用。這項(xiàng)工作加深了對SGD優(yōu)化過程的理解，也有助于構(gòu)建深度神經(jīng)網(wǎng)絡(luò)的訓(xùn)練理論。

梯度下降是機(jī)器學(xué)習(xí)算法中最常用的一種優(yōu)化方法。

其中，隨機(jī)梯度下降 (Stochastic Gradient Descent, SGD) 由于學(xué)習(xí)速率快并且可以在線更新，常被用于訓(xùn)練各種機(jī)器學(xué)習(xí)和深度學(xué)習(xí)模型，很多當(dāng)前性能最優(yōu) (SOTA) 模型都使用了SGD。

然而，由于SGD 每次隨機(jī)從訓(xùn)練集中選擇少量樣本進(jìn)行學(xué)習(xí)，每次更新都可能不會按照正確的方向進(jìn)行，因此會出現(xiàn)優(yōu)化波動(dòng)。

對于非凸函數(shù)而言，SGD就只會收斂到局部最優(yōu)點(diǎn)。但同時(shí)，SGD所包含的這種隨機(jī)波動(dòng)也可能使優(yōu)化的方向從當(dāng)前的局部最優(yōu)跳到另一個(gè)更好的局部最優(yōu)點(diǎn)，甚至是全局最優(yōu)。

在密蘇里科技大學(xué)與百度大數(shù)據(jù)實(shí)驗(yàn)室日前合作公開的一篇論文中，研究人員利用概率論中的大偏差理論對SGD在深度神經(jīng)網(wǎng)絡(luò)訓(xùn)練過程中的行為進(jìn)行了刻畫。

“這項(xiàng)工作的出發(fā)點(diǎn)在于試圖理解SGD的優(yōu)化過程和GD有什么不同，尤其是SGD的隨機(jī)項(xiàng)（也是GD所沒有的）在隱式正則化中到底起到什么作用。”論文第一作者、密蘇里科技大學(xué)數(shù)學(xué)系助理教授胡文清博士在接受新智元采訪時(shí)說。

“通過變分分析和構(gòu)造勢函數(shù)，我們發(fā)現(xiàn)，由于有方差 (variance) 的存在，對于任何局部最優(yōu)而言，SGD都有一定逃逸的可能性。”研究負(fù)責(zé)人、百度大數(shù)據(jù)實(shí)驗(yàn)室科學(xué)家浣軍博士告訴新智元：“如果時(shí)間足夠長，SGD會以馬氏鏈的方式遍歷所有的局部最優(yōu)，最終達(dá)到一個(gè)全局最優(yōu)。”

“對于過參數(shù)化網(wǎng)絡(luò) (over parameterized network)，全局最優(yōu)的點(diǎn)在任何數(shù)據(jù)點(diǎn)的梯度都是0。SGD就會被限制在這樣的位置上。”

不同梯度下降優(yōu)化方法在損失曲面鞍點(diǎn)處的表現(xiàn)，過參數(shù)化網(wǎng)絡(luò)的全局最優(yōu)點(diǎn)在任何數(shù)據(jù)點(diǎn)的梯度都是0，SGD就會被限制在這樣的位置上。

這項(xiàng)工作有助于我們更深刻地理解SGD在訓(xùn)練深度神經(jīng)網(wǎng)絡(luò)過程，以及訓(xùn)練其它機(jī)器學(xué)習(xí)模型中的機(jī)制和作用。

擬勢函數(shù)：隨機(jī)梯度下降中損失函數(shù)的隱式正則項(xiàng)

人們普遍認(rèn)為SGD是一種“隱式正則項(xiàng)”，能夠自己在模型或數(shù)據(jù)集中尋找一個(gè)局部最小點(diǎn)。

此前有研究從變分推斷的角度分析SGD逃離bad minima的現(xiàn)象。還有研究發(fā)現(xiàn)，SGD的逃逸速率跟噪聲協(xié)方差有關(guān)，尤其是在深度神經(jīng)網(wǎng)絡(luò)模型中。

在這篇題為《將擬勢函數(shù)視為隨機(jī)梯度下降損失函數(shù)中的隱式正則項(xiàng)》的論文中，作者提出了一種統(tǒng)一的方法，將擬勢作為一種量化關(guān)系的橋梁，在SGD隱式正則化與SGD的隨機(jī)項(xiàng)的協(xié)方差結(jié)構(gòu)之間建立了聯(lián)系。

“從‘?dāng)M勢’這種統(tǒng)一的觀點(diǎn)出發(fā)，能更清楚地從數(shù)學(xué)上描述SGD的長時(shí)間動(dòng)力學(xué)。”胡文清博士說。

具體說，他們將隨機(jī)梯度下降 (SGD) 的變分推斷看做是一個(gè)勢函數(shù)最小化的過程，他們將這個(gè)勢函數(shù)稱之為“擬勢函數(shù)”(quasi–potential)，用(全局)擬勢φQP表示。

這個(gè)擬勢函數(shù)能夠表征具有小學(xué)習(xí)率的SGD的長期行為。研究人員證明，SGD最終達(dá)到的全局極小值點(diǎn)，既依賴于原來的損失函數(shù)f，也依賴于SGD所自帶的隨機(jī)項(xiàng)的協(xié)方差結(jié)構(gòu)。

不僅如此，這項(xiàng)工作的理論預(yù)測對于一般的非凸優(yōu)化問題都成立，揭示了SGD隨機(jī)性的協(xié)方差結(jié)構(gòu)在其選擇最終的全局極小值點(diǎn)這個(gè)動(dòng)力學(xué)過程的關(guān)鍵性作用，進(jìn)一步揭示了機(jī)器學(xué)習(xí)中SGD的隱式正則化的機(jī)制。

下面是新智元對論文凸損失函數(shù)相關(guān)部分的編譯，點(diǎn)擊“閱讀原文”查看論文了解更多。

局部擬勢：凸損失函數(shù)的情況

我們假設(shè)原來的損失函數(shù)f(x)是凸函數(shù)，只允許一個(gè)最小點(diǎn)O，這也是它的全局最小點(diǎn)。設(shè)O是原點(diǎn)。

我們將在這一節(jié)中介紹局部準(zhǔn)勢函數(shù)，并通過哈密頓-雅可比型偏微分方程將其與SGD噪聲協(xié)方差結(jié)構(gòu)聯(lián)系起來。分析的基礎(chǔ)是將LDT解釋為軌跡空間中的路徑積分理論。

SGD作為梯度下降(GD)的一個(gè)小隨機(jī)擾動(dòng)

首先，我們給出一個(gè)假設(shè)：

假設(shè)1：假設(shè)損失函數(shù)f(x)允許梯度?f(x)，即L–Lipschitz：

(1)

我們假設(shè)Σ(x)是x中的分段Lipschitz，并且SDG協(xié)方差矩陣D(x)對于所有x∈Rd是可逆的，使得：

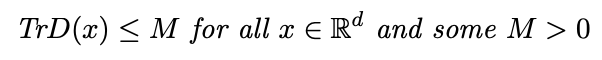
(2)

對于ε＞0，SGD過程具有接近由如下確定性方程表征的梯度下降（GD）流的軌跡：

(3)

事實(shí)上，我們可以很容易地證明有以下內(nèi)容：

引理1：基于假設(shè)1，我們有，對于任何T＞0，

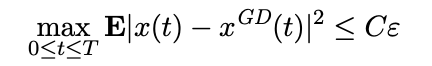
(4)

對一些常數(shù)C = C(T, L, M) > 0。

當(dāng)上述公式成立時(shí)，我們可以很容易得出在區(qū)間0≤t≤T內(nèi)，x(t)和xGD(t)收斂于。因此，在有限的時(shí)間內(nèi)，SGD過程x(t)將被吸引到原點(diǎn)O的鄰域。

由于O是凸損失函數(shù)f(x)的唯一最小點(diǎn)，R中的每一點(diǎn)都被梯度流Rd吸引到O。

在僅有一個(gè)最小點(diǎn)O的情況下，也可以執(zhí)行由于小的隨機(jī)擾動(dòng)而對吸引子(attractor)的逃逸特性的理解。

大偏差理論解釋為軌跡空間中的路徑積分

為了定量地描述這種逃逸特性，我們建議使用概率論中的大偏差理論(LDT)。粗略地說，這個(gè)理論給出了路徑空間中的概率權(quán)重，而權(quán)重的指數(shù)部分由一個(gè)作用量泛函S給出。

局部擬勢函數(shù)作為變分問題和哈密頓-雅可比方程的解

我們可以定義一個(gè)局部擬勢函數(shù)為：

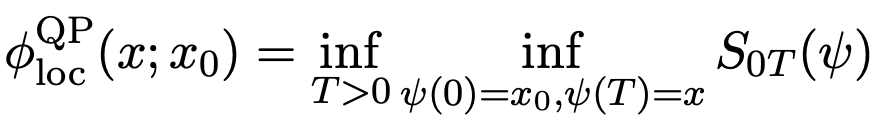
(5)

將公式(5)和下面的公式6)進(jìn)行結(jié)合

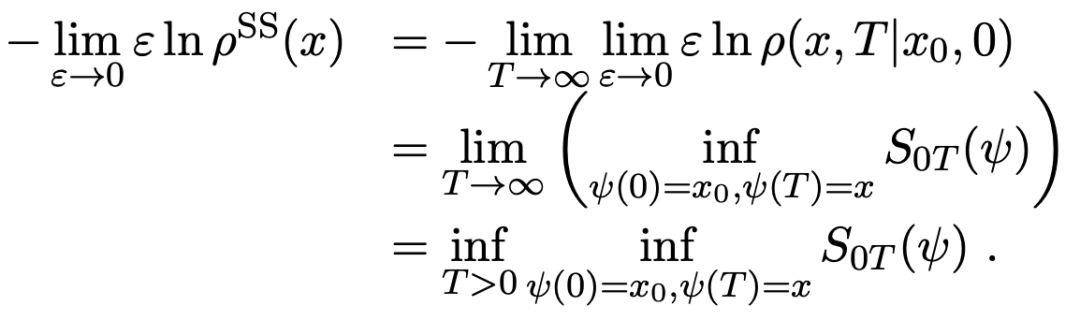
(6)

給出了平穩(wěn)測度的指數(shù)漸近：

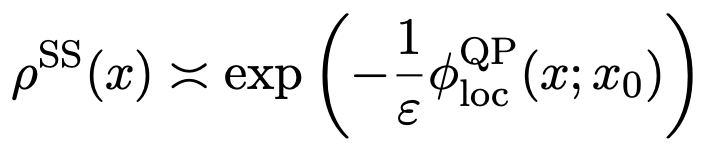
(7)

這意味著在梯度系統(tǒng)只有一個(gè)穩(wěn)定吸引子O的情況下，擬勢φQP(x)是由局部φQPloc(x；x0)給定，這是變分問題(公式5)的解。

局部最小點(diǎn)的逃逸屬性(根據(jù)局部擬勢)

局部擬勢φQPloc(x；x0)的另一個(gè)顯著特征是它描述了局部最小點(diǎn)的逃逸性質(zhì)。從sharp極小值到flat極小值的逃逸是導(dǎo)致良好泛化的一個(gè)關(guān)鍵特征。

LDT估計(jì)提供了一種工具，可以獲得退出概率的指數(shù)估計(jì)值，并從吸引子獲得平均首次退出時(shí)間。

并且我們可以證明一個(gè)過程x(t)在局部最小點(diǎn)處的逃逸性質(zhì)，如出口概率、平均逃逸時(shí)間甚至第一個(gè)出口位置，都與擬勢有關(guān)。

全局?jǐn)M勢：SGD在各個(gè)局部極小值點(diǎn)之間的馬氏鏈動(dòng)力學(xué)

現(xiàn)在再假設(shè)損失函數(shù)f(x)是非凸的，存在多個(gè)局部極小值點(diǎn)。這種情況下，對每個(gè)局部極小值點(diǎn)的吸引區(qū)域，都可數(shù)學(xué)上構(gòu)造由前述所介紹的局部擬勢。

SGD在進(jìn)入一個(gè)局部極小值點(diǎn)之后，會在其協(xié)方差結(jié)構(gòu)所帶來的噪聲的作用下，逃逸這個(gè)局部極小值點(diǎn)，從而進(jìn)入另一個(gè)局部極小值點(diǎn)。

按照前述的介紹，這種逃逸可以由局部擬勢給出。然而在全局情形，不同的極小值點(diǎn)之間的局部擬勢不一樣，而從一個(gè)極小值點(diǎn)到另一個(gè)極小值點(diǎn)之間的這種由逃逸產(chǎn)生的躍遷，會誘導(dǎo)一個(gè)局部極小值點(diǎn)之間的馬氏鏈。

我們的文章指出，SGD的長時(shí)間極限行為，正是以這種馬氏鏈的方式，遍歷可能的局部極小值點(diǎn)，最終達(dá)到一個(gè)全局極小值點(diǎn)。

值得一提的是，這個(gè)全局極小值點(diǎn)不一定是原來損失函數(shù)的全局極小值點(diǎn)，而是和SGD的隨機(jī)性的協(xié)方差結(jié)構(gòu)有關(guān)，這一點(diǎn)可以由上節(jié)中局部擬勢的構(gòu)造方式看出。

這就表明SGD的隨機(jī)性所產(chǎn)生的協(xié)方差結(jié)構(gòu)，影響了其長期行為以及最終的全局極小值點(diǎn)的選擇。

文章中給出了一個(gè)例子，說明當(dāng)損失函數(shù)f(x)有兩個(gè)完全對稱的全局極小值點(diǎn)，而其所對應(yīng)的協(xié)方差結(jié)構(gòu)不同的情況下，SGD會傾向于選擇其中一個(gè)全局極小值點(diǎn)，這一個(gè)極小值點(diǎn)對應(yīng)的協(xié)方差結(jié)構(gòu)更接近各向同性(isotropic)。

未來工作

研究人員希望通過這項(xiàng)工作，進(jìn)一步理解SGD所訓(xùn)練出的局部極小點(diǎn)的泛化性能，特別是泛化能力與協(xié)方差結(jié)構(gòu)的關(guān)系。基于此，他們期待進(jìn)一步的結(jié)果將不僅僅局限于overparametrized神經(jīng)網(wǎng)絡(luò)，而對一般的深度學(xué)習(xí)模型都適用。