摘要
本文匯集了開環增益,閉環增益,增益和相位裕度,最小增益穩定性的思想,并展示了這些參數在反饋系統中如何相互關聯。它根據理論控制系統以及包括線性穩壓器在內的實際電子電路來檢查環路增益。
介紹
鮑勃·多布金(Bob Dobkin)在2014年的《解決舊問題的新型線性穩壓器》一文中描述了突破性的LT3081低壓降線性穩壓器,表明其恒定環路增益比其他LDO解決方案改善了瞬態響應和絕對輸出電壓精度。該陳述雖然令人印象深刻且真實,但卻為工程師對環路增益的理解做出了重要假設,并且恒定環路增益與LT3081的優勢之間有著明確的聯系。不幸的是,環路增益不像閉環和開環增益那樣普遍被認可。
如果不了解環路增益及其對電子電路的影響,就無法真正理解LT3081的優勢。本文面向電源工程師,研究了環路增益對增益和相位裕度的影響,并將其與理論控制系統和實際模擬反饋電路相關聯。
基礎
經典的模擬構建塊是運算放大器,其行為可以應用于大多數反饋控制系統。實際上,可以通過將許多器件建模為運算放大器來簡化其性能。我們可以將運算放大器理論應用于低壓差線性穩壓器(LDO)和開關穩壓器,以預測器件的穩定性。圖1顯示了簡化的運算放大器電路。
圖1.簡化的運算放大器電路
輸入電壓被施加到誤差放大器,該誤差放大器從VIN減去輸出電壓的一部分(β)以產生誤差信號。因此錯誤是
![]()
該誤差信號經過放大器(A0)的開環增益以產生輸出電壓:
![]()
重新安排它以查找放大器的閉環增益:
![]()
在大多數運算放大器電路中,放大器的開環增益非常高,即比分母中的“ 1”大得多,從而使閉環增益近似為:
![]()
圖2顯示了傳統的運算放大器電路,其中可預測的操作取決于該增益近似值。
圖2.傳統運算放大器電路
對于輸出端的任何給定電壓,如果開環增益是無限的,則兩個輸入引腳之間的電壓差(VDIFF)為零,并且運放進行調節以使其兩個輸入引腳保持相同的電壓。此處,輸出通過電阻分壓器R1-R2反饋到輸入,因此反饋分數(β)為0.1(1k / 10k)。根據上面的公式,如果開環增益很高,則電路的閉環增益近似于反饋分數的倒數,因此電路的閉環增益為10。
這種簡化的運算放大器理論可用于對各種電路進行建模,適用于低頻輸入,但這種簡單的模型在高頻輸入時會失去有效性。
AC的環路增益和運算放大器
LT1012運算放大器具有經典的開環增益與頻率響應的關系,如圖3所示。
圖3. LT1012運算放大器開環和閉環增益與頻率的關系
在圖3中,您可以看到開環增益在輸入頻率高達0.3Hz時很大,然后以每十倍20dB的速率衰減。盡管增益在很寬的輸入頻率范圍內仍保持很高的水平,但有一點開環增益不能認為是相對無限的。也就是說,當開環增益接近閉環增益時,上述理想的運算放大器模型以及我們對其性能所做的相應假設就開始失去可信度。
考慮圖2中有限的開環增益對電路的閉環增益的影響。反饋分數(β)為1/10,因此在理想的運放模型中,閉環增益是該值的倒數,或10.如果我們的運算放大器的開環增益為100,則計算出的閉環增益為
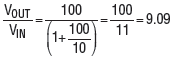
計算的閉環增益
增益仍約為10,但誤差為9%。
現在考慮使用相同的放大器,但具有單位增益反饋。反饋分數(β)為1,因此理想的運算放大器閉環增益應為該值的倒數,或者為1。如果我們的運算放大器的開環增益為100,則閉環增益為

盡管這兩個電路的開環增益相同,但僅通過減小閉環增益就可以將增益誤差減小到1%。
上面的等式顯示了該錯誤是如何大βA的函數0是相對于在分母中“1”的術語。請注意,開環增益本身并不總是確定誤差,但重要的是開環增益(A0)與反饋分數(β)的乘積。對于大型βA0中,“1”一詞失去意義;對于βA0接近統一,“1”變成顯著,增加了錯誤。
什么是βA0
那么,什么是βA0?在圖3中,在對數刻度上,閉環曲線(大約1 /β)和開環曲線(A0)之間的差為

這樣的開環增益曲線和閉環增益曲線之間的間隙為βA0(約105分貝在DC)。參見圖1中,我們可以看到,0?β是增益通過放大器和反饋回路去,所以βA0是我們的環路增益,并在系統中可用的額外增益的表示。盡管通常認為放大器的開環增益應該較高才能使運算放大器增益準確,但是我們可以看到不一定是開環增益,而是必須較高。換句話說,開環增益必須比閉環增益高,才能獲得準確的電路增益。
那么,有限的開環增益對運算放大器電路有什么影響?基本運算放大器理論指出,兩個輸入電壓都調節到相同的電壓,這是在非常高的開環增益下的適當假設,但是當開環增益隨信號頻率的增加而降低時會發生什么呢?
考慮圖2的電路,隨著放大器的開環增益隨輸入頻率的增加而減小,我們看到兩個輸入引腳之間的交流電壓增加,等于輸出電壓除以開環增益。這不是輸入失調電壓,而是一個小的交流電壓(VDIFF),等于輸出電壓除以放大器的開環增益。如果開環增益為一百萬,并且輸出為1V,則兩個輸入引腳之間的VDIFF為1μV。隨著輸入頻率的升高和開環增益的降低,VDIFF增大。極端的情況是,開環增益已降至10,我們的VDIFF變為100mV。
這就是許多人誤解了運算放大器在較高AC頻率下的操作的原因,因為這兩個輸入引腳不再調節為相同的電壓。兩個輸入引腳之間的電壓由DC輸入失調電壓(為簡單起見,在此忽略)和VDIFF組成。VDIFF通常可以忽略不計,但在高頻時則不能忽略。
我們知道開環增益由
![]()
我們知道β表示為

其中V–是反相輸入端的電壓,因此環路增益為
![]()
環路增益將V–(應等于輸入信號)與VDIFF進行比較。
相移的影響
還存在與VDIFF相關的相移。圖3的開環增益曲線與低通濾波器的響應相同。在0.3Hz處有一個中斷頻率,此后增益以每十倍頻20dB衰減,另一個在1MHz,然后以十倍頻40db衰減。圖4顯示了具有相同中斷頻率的低通濾波器。
圖4.具有與圖2中的開環增益曲線相匹配的頻率響應的低通濾波器
單階低通濾波器(由R1和C1組成)的傳遞函數由下式給出:
![]()
根據經驗,對于單階低通濾波器,在中斷頻率的十分之一處,相移大約為零。在每個中斷頻率處,相移都為–45°(相位滯后),而在中斷頻率的十倍時,相移約為–90°,并保持在此范圍之外。如果第二個中斷頻率為1MHz,那么在100kHz時,濾波器的總相移約為–90°,在1MHz時,總相移為–135°,而在10MHz時,總相移約為–180°。
由于放大器的開環增益以相同的方式工作,盡管圖2的輸入和輸出電壓是同相的,但VDIFF和VOUT之間存在一個相移,這與放大器的開環增益的相移有關。放大器。同樣,由于VDIFF通常很小,我們可以忽略它,但是隨著輸入頻率的增加,與輸入電壓異相的VDIFF增加會導致穩定性問題。圖3的開環增益曲線沒有穩定性問題,但是可以想象,如果第二個中斷頻率的頻率遠低于1MHz,那么我們的電路現在的VDIFF將會增加。可能與輸入電壓異相180°,這肯定會影響穩定性。
LTspice是分析各種頻率下相移影響的有用工具。圖5a顯示了輸出電壓在1kHz時滯后VDIFF90°。
圖5a。VOUT在1kHz時相位滯后VDIFF90°
如果輸入頻率從1kHz增加到10kHz,則VDIFF增大10倍,但相位滯后仍保持90°,這表明我們離開環增益的第二個斷開頻率還差得很遠。如圖5b所示。當輸入頻率接近1MHz時,相位滯后開始增加到90°以上,并且VDIFF相應增加。
圖5b。VOUT在10kHz時相位滯后VDIFF90°
因此可以看出,VDIFF可能會達到一個與輸入電壓相當的值,并且與輸入電壓異相180°—為了使電路振蕩,環路周圍的增益必須為單位且相移環路周圍必須為180°。如果VDIFF經受放大器(A的開環增益0),則該反饋網絡的衰減,(β)中,我們可以看到,它是環路增益(βA0)和它的相位決定的穩定性系統的。
考慮圖2中的電路,運算放大器放大其輸入(V之間的電壓DIFF)并且這被進行增益βA的0在V產生電壓-。如果環路增益為1,這意味著在V的電壓-是相同的為VDIFF,從而V的振幅DIFF并沒有改變,因為它已經通過循環通過。如果已經經歷了180°的相移并且VDIFF的幅度沒有改變,則電路將振蕩。純粹主義者可能會辯稱相移必須為360°,而額外的180°由反相輸入引腳提供。
附帶說明一下,如果圖2中的電路具有高增益,則意味著反饋電阻器會大量衰減輸出電壓。大多數相移發生在放大器中(因為反饋電阻沒有電抗成分,因此不存在相移),因此增益越低,反相輸入端出現的輸出電壓就越“相移”,從而增加了可能性。不穩定。這就是為什么某些放大器具有最小增益穩定性的原因。如果將增益降低到某個點以下,則更多的相移輸出電壓會出現在反相端,因此電路更容易振蕩。
對于各種環路增益和相移,值得考慮圖2中電路的操作。
在低頻下,當放大器具有足夠的環路增益時,與反相輸入端的電壓(V–)相比,VDIFF很小,并且相移為–90°。在這種情況下,反相輸入端的電壓會淹沒VDIFF,因此可以忽略VDIFF。但是,如果VDIFF相對于V–的相移為–180°,并且在環路中存在增益,我們可以看到,VDIFF處的任何電壓在繞環路傳播并反轉,然后被放大和反向,因此電路振蕩。該電路只需要具有統一的環路增益即可維持振蕩。VDIFF有多接近當電路具有統一的環路增益時,它會變為–180°,這是電路相位裕度的量度,它告訴我們電路相位接近不穩定點的程度。相移為–120°的電路具有60°的相位裕度。
同樣,如果VDIFF相對于V–具有–180°的相移,但是在通過環路時會發生衰減,則回到V–的電壓會較小,因此,由于缺少V,FF會停止任何潛在的振蕩環路增益。VDIFF穿過環路時會經歷多少衰減(當相移為–180°時)是電路增益裕度的量度,它告訴我們當相移為0時,電路的環路增益比單位增益低多少。 –180°。當VDIFF為–180°時,環路中的衰減為10dB的電路的增益裕度為10dB。
以上所有內容都可以與控制理論和圖1的框圖相關聯。我們知道,反饋系統的閉環增益由下式給出:
![]()
其中βA0是系統的環路增益。如果βA0具有-180°和單位增益的相移,分母在一個特定的頻率變為零,并且電路在該頻率振蕩。如果βA0是大的,但不具有-180°的相移,分母不為零,電路不振蕩,我們有足夠的相位裕度。同樣地,如果βA0小于單位但具有-180°的相移,該電路不振蕩,我們有足夠的增益裕量。
因此,現在我們可以看到,我們具有相關的開環增益,閉環增益,環路增益,增益裕度和相位裕度,并在控制理論領域和電路理論領域對此進行了解釋。
那么這與電源電路有什么關系呢?大多數電源系統都可以建模為運算放大器電路。圖6顯示了LT1086線性穩壓器。我們可以看到該電路有兩個反饋電阻,它們為ADJ引腳(內部運算放大器的反相輸入)提供一部分輸出電壓。同相端連接到內部參考電壓。
圖6.傳統線性穩壓器(LT1086)
如上所述,放大器增益的精度取決于放大器的環路增益:放大器中的環路增益越高,則意味著增益精度越高。
增加LT1086的輸出電壓等同于增加運算放大器的閉環增益。圖7顯示了將閉環增益從20dB增加到80dB的效果。如果環路增益由開環增益曲線和閉環增益曲線之間的差異表示,則增加LT1086的輸出電壓會降低環路增益,從而降低輸出電壓的絕對精度。增加輸出電壓的另一個缺點是降低了電路的頻率響應(在這種情況下,從100kHz降至100Hz),因此負載瞬態響應會受到影響。
圖7.電壓增益與頻率的關系
線性穩壓器LT308x系列將傳統的LDO架構更改為圖8所示的架構。
圖8. LT3080線性穩壓器使用非常規架構來提高精度和瞬態響應
LT3080使用一個內部電流源在一個外部電阻RSET兩端產生一個電壓。然后將此電壓施加到單位增益緩沖器以產生輸出電壓。這具有許多含義。
內部運算放大器以恒定的單位閉環增益工作,輸出電壓由運算放大器“輸入”處的RSET電阻值設定。
將圖7中所示的LT3080與圖6中所示的傳統運算放大器電路進行比較。圖6中LT1086的輸出電壓是通過改變LT1086的反饋電阻器(從而改變了閉環增益)來改變的。將其與以恒定閉環增益工作的LT3080相比,在LT3080上,通過RSET兩端的電壓來設置放大器的“輸入”電壓。如果閉環增益保持不變,則環路增益保持不變,因此即使在高輸出電壓下,該電路也具有良好的絕對精度。順便提及,這就是為什么DC / DC轉換器中的環路補償組件始終具有串聯電容的原因。誤差放大器的輸出為電流源,直流電的串聯電容為高阻抗,因此在補償環路的直流電時產生高環路增益。
保持環路增益不變的另一個結果是,頻率響應保持不變,并且在高輸出電壓下不會犧牲,因此該器件能夠快速響應負載瞬變。
考慮到不斷降低的電源電壓,另一個好處是,LT308x部件可以產生低至0V的輸出電壓。傳統的LDO不能將其輸出電壓設置為低于內部基準電壓,而通過將LT308x上的RSET短路,可以將輸出電壓設置為低至0V。
結論
LT308x系列LDO由于具有恒定的高環路增益,因此具有比傳統LDO更高的高輸出電壓精度和瞬態響應。它們還可以以傳統LDO無法使用的方式使用,例如將輸出設置為0V,或使其并聯以實現更高的電流工作。
-
增益
+關注
關注
3文章
377瀏覽量
36855 -
模擬控制
+關注
關注
1文章
32瀏覽量
15109
原文標題:5G真的要來了,這一次,別輸在起跑線上
文章出處:【微信號:hbrchinese,微信公眾號:哈佛商業評論】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
控制系統的三種信號_控制系統的三個指標
TPS546D24/A輸出電容選取以及布局對環路增益的影響

AMC7891高集成,低功率,完全模擬監控和控制系統數據表





 環路增益以及它對模擬控制系統的影響
環路增益以及它對模擬控制系統的影響

















評論