鑒于直接轉子磁場定向矢量控制系統較為復雜、磁鏈反饋信號不易獲取等缺點,而轉差頻率矢量控制方法是按轉子磁鏈定向的間接矢量控制系統,不需要進行磁通檢測和坐標變換,并具有控制簡單、控制精度高、具有良好的動、靜態性能等特點。在分析其控制原理的基礎上,應用 Matlab/Simulink軟件構建了轉差頻率矢量控制的異步電機調速系統仿真模型,并通過各模塊閩的參數配合調節與優化,對其進行了仿真分析。仿真結果驗證了,采用轉差頻率矢量控制的調速系統具有良好的控制性能。
引言
基于轉差頻率控制的矢量控制方式是在進行U/f恒定控制的基礎上,通過檢測異步電動機的實際速度n,并得到對應的控制頻率f,然后根據希望得到的轉矩,分別控制定子電流矢量及兩個分量間的相位,對輸出頻率f進行控制的。采用這種控制方法可以使調速系統消除動態過程中轉矩電流的波動,從而在一定程度上改善了系統的靜態和動態性能,同時它又具有比其它矢量控制方法簡便、結構簡單、控制精度高等特點。
Simulink仿真系統是Matlab最重要的組件之一,系統提供了標準的模型庫,能夠幫助用戶在此基礎上創建新的模型庫,描述、模擬、評價和細化系統,從而達到系統分析的目的。
1 轉差頻率矢量控制系統
1.1 數學模型
轉差頻率矢量控制是按轉子磁鏈定向的間接矢量控制系統,不需要進行復雜的磁通檢測和繁瑣的坐標變換,只要在保證轉子磁鏈大小不變的前提下,通過兩相同步旋轉坐標系(M-T坐標系)上的數學模型運算就可以實現間接的磁場定向控制。其控制的基本方程式如下:
電壓方程:

式中:usm,ust,urm,urt為定、轉子在M-T軸上的電壓分量;Ls為定子自感;Lr為轉子自感;Lm為定、轉子互感;ω1為定子角頻率、ωs為轉差角頻率;P為微分算子;Rs,Rr為定、轉子電阻。
磁鏈方程為:
?

式中:ψsm,ψrm為定、轉子磁鏈勵磁分量;ψst,ψrt為定、轉子磁鏈轉矩分量;
M-T坐標上的電磁轉矩方程:
?

式中:np為轉子極對數;Te為電磁轉矩。
當按轉子磁鏈定向時,應有ψrm=ψr,ψrt=0,代入以上3個方程中,即得:
?

式中:M為定、轉子互感系數;ψr為轉子總磁鏈;Tr為轉子電磁時間常數,Tr=Lr/Rr。異步電動機轉矩為:

??? 當電機穩態運行時,S很小,因此很小,轉矩的近似表達式為:
?

由
由式(9)可見,只要能保證φm不變,控制ω。即可控制Te,從而間接地控制電機的轉速。
1.2 轉差頻率矢量控制系統結構
基于轉差頻率控制的異步電動機矢量控制調速系統原理如圖1所示。主電路采用SPWM電壓型逆變器,即異步電動機定子角頻率ω1由轉子角頻率ω和轉差角頻率ωs組成(ω1=ω+ωs)。
矢量控制技術自從上世紀60、70年代開始,國內外眾多專家學者就已經進行了潛心的研究,因此,矢量控制技術發展至今,內容已經非常豐富。本文只討論基于轉子磁場定向的矢量控制原理。
該控制系統所檢測的兩相定子電流經Clarke與Park變換后可產生轉矩電流分量和勵磁電流分量,然后結合檢測轉速并通過電流模型計算坐標變換所需的磁鏈角。檢測轉速與給定轉速誤差經PI調節后將生成轉矩給定值。轉矩電流分量與勵磁電流分量的誤差經PI調節可產生u小M。給定值,并在通過旋轉坐標變換后輸入SVPWM模塊以產生6路PWM波,從而控制逆變器。
?
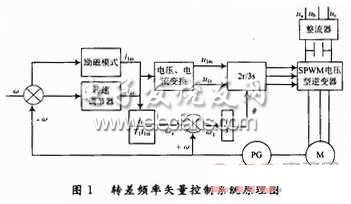
圖1中:ω、-ω分別為轉子角頻率給定和轉子角頻率負反饋;i1m、i1t分別為定子電流的轉矩分量和勵磁分量;ω1、+ω分別為定子角頻率和轉子角頻率正反饋;u1m、u1t分別為定子電壓的轉矩分量和勵磁分量;
根據基本方程,以及圖1可以看出,在保持轉子磁鏈ψr不變的情況下,電動機轉矩直接受定子電流的轉矩分量ist控制,并且轉差角頻率ωs可以通過定子電流的轉矩分量ist計算。如果采用磁通不變的控制,則Pψr=0,由式(7)可得ψrm=Lmirm,代入式(6),得 ωs=ist/(Trism)。
由于矢量控制方程得到的是定子電流的勵磁分量和轉矩分量,而本系統采用電壓型逆變器,需要將電流的控制方式轉換為電壓控制。由于 ψrm=Lmirm,ψrt=0,而變頻調速時電動機轉子短路即urm=urt=O,將其代入式(1),并展開可得定子電壓的勵磁分量usm和轉矩分量 ust,其變換關系為:
?

2 轉差頻率矢量控制調速系統仿真與研究
2.1 仿真模型的建立
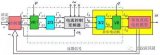
根據轉差頻率矢量控制系統的原理框圖,采用Matlab/Simulink軟件構建轉差頻率矢量控制調速系統模型如圖2所示。圖中控制部分由給定、PI轉速調節器、函數運算、兩相/三相坐標變換、PWM脈沖發生器等環節組成。
?

2.2 仿真與結果分析
2.2.1 模型參數
模型參數主要有電機模型參數、控制系統放大器參數、給定值模塊參數、限幅模塊參數等,其中電機參數設定為:額定電壓UN=380 V;頻率fN=50 Hz;極對數P=2;定子電阻Rs=O.435 Ω;額定功率PN=25 kW;轉子電阻Rr=O.435 Ω;定、轉子互感Lm=O.069 H;轉動慣量J=O.19 kg·m2;轉矩給定值;逆變器直流電壓510 V;定子繞組自感Ls=0.071 H;轉子繞組自感Lr=0.071 H;漏磁系數;轉子時間常數Tr=Lr/R=O.087。其它參數:勵磁電流給定值;額定轉速n*=1400r/min。仿真時間設定為0.6 s。
將參數代入式(6),式(10),式(11)中可得Usm,Ust和ωs函數表達式為:
?

?
式中:u(1)、u(2)、u(3)為模塊參數變量,分別代表ism,ist,ω1。
2.2.2 仿真結果分析
在此采用ODE5算法對系統進行仿真。在啟動O.5 s時加載TL=65 N·m,其仿真波形如圖3所示。
?

從仿真結果中可以得到電機在起動和加載過程中,轉速、電流、電壓和轉矩的變化過程。圖3(a)中可以看到,轉速隨時間的變化逐漸增大。當t=O.361 s時,轉速達到額定轉速1400 r/rain左右,而當t=O.5 s時,由于此時電動機開始加載,隨后趨于穩定。圖3(e)與圖3(f)分別反映了電動機在起動過程中定子繞組產生的旋轉磁場和電動機的轉矩一轉速特性,圖3(e)可以看出,定子磁鏈的軌跡一開始并不規則,而且在不斷變化,但是隨著時間的變化,磁鏈軌跡開始呈現規則圖形,保持穩定,這是因為電動機在零狀態起動時,電動機磁場有一個建立過程,在建立過程中磁場變化是不規則的,隨著時間的推移,磁場逐漸規則如圖3(e)所示。而磁場的變化則會影響轉矩的變化,圖3(f)所示轉矩在一開始即電動機零狀態起動時,大幅度變化,當磁場變化逐漸規則時,轉矩變化也開始在小范圍內波動,幾乎保持穩定。電動機的轉矩一轉速特性反映了通過矢量控制能使電動機保持恒轉矩起動,并且調節ASR的輸出限幅可以改變最大輸出轉矩。
3 結語
系統中PI調節器的比例系數K1、積分系數K2與坐標變換模塊輸出信號的放大系數需要配合調節,當偏差較大時,調節K1,以快速減少偏差;當偏差達到要求后,調節K2,以消除穩態誤差。同時要配合調節坐標變換模塊輸出信號的放大系數,這樣才能保證PWM發生器輸出正確的三相調制信號波形。
 電子發燒友App
電子發燒友App












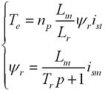











評論