在計算機中,需要對小數進行計算,因此需要相應的電路支持。支持小數計算的電路有兩種:定點部件和浮點部件。定點部件與整數部件沒有本質區別,只是要假設有一個小數點存在于某兩位數之間,計算時需要把小數點對齊[1]。本文首先介紹浮點數標準IEEE754,為后續浮點部件的電路設計做好理論基礎。
一、名詞解釋
IEEE(Institute of Electrical and Electronics Engineers)[2]:電氣和電子工程師協會。作為一個電子類工程師,必須對其有所了解,可以說對她的了解是基本的行業素質。話說:一流的企業做標準,二流的企業做品牌,三流的企業做產品,IEEE致力于電氣、電子、計算機工程和與科學有關的領域的開發和研究,在太空、計算機、電信、生物醫學、電力及消費性電子產品等領域已制定了900多個行業標準,現已發展成為具有較大影響力的國際學術組織。
IEEE754[3]:IEEE 754標準IEE浮點數算術標準(IEEE Standard for Floating-Point Arithmetic)的標準編號,等同于國際標準ISO/IEC/IEEE 60559。該標準由美國IEEE計算機學會旗下的微處理器標準委員會(Microprocessor Standards Committee, MSC)發布。IEEE 754 標準規定了計算機程序設計環境中的二進制和十進制的浮點數自述的交換、算術格式以及方法。
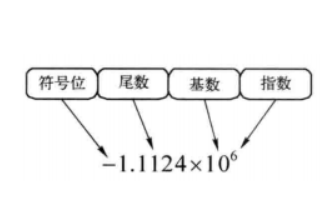
浮點數[4]:浮點數是屬于有理數中某特定子集的數的數字表示,在計算機中用以近似表示任意某個實數。具體的說,這個實數由一個整數或定點數(即尾數)乘以某個基數(計算機中通常是2)的整數次冪得到,這種表示方法類似于基數為10的科學計數法。
二、單精度浮點數標準
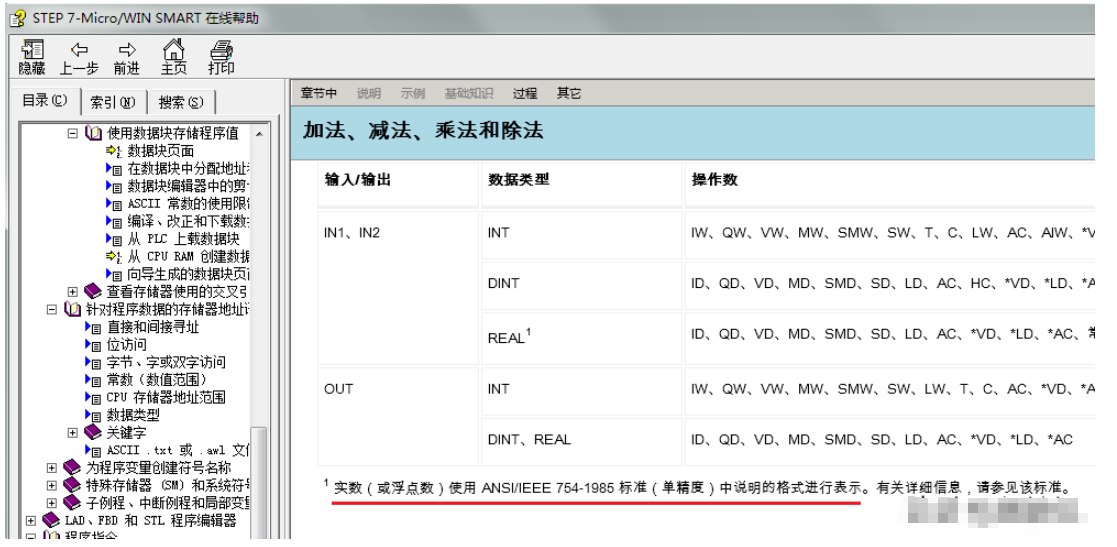
IEEE754標準[5]主要定義了單精度和雙精度這兩種浮點數的格式。單精度浮點數用32位二進制數來表示,而雙精度浮點數則用64位,雙精度浮點數相對于單精度浮點數主要的作用在于提高了精度。由于單精度浮點數和雙精度浮點數標準定義基本相同,這里只介紹單精度浮點數格式。
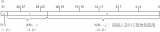
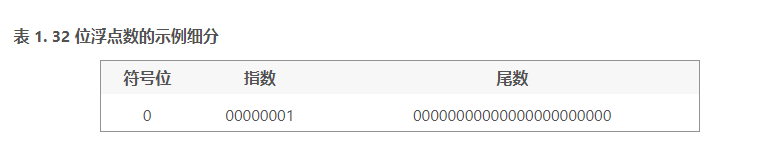
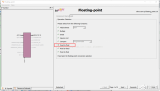
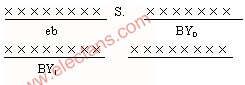
IEEE754標準32位單精度浮點數格式由三部分組成:第31位是符號位s(Sign),0表示正數,1表示負數;第30~23位是8位階碼位e(Exponent),用移碼表示,其偏移量為127;第22~0位是23位尾數f(Fraction),用原碼表示。如下圖1所示:
圖1.IEEE754單精度浮點數格式
如果0 < e < 255,單精度浮點數的值為(-1)s×2e-127×1.f,我們稱其為規格化數。需要注意的是1.f中的1稱為隱藏位,其并不占用32位中的任何一位。例如下面這個浮點數:
1_01111111_11000000000000000000000
該浮點數值為(-1)1×2127-127×1.11 = -(1+0,5+0,25) = -1.75。
上述是規格化浮點數格式,以下有幾種非規格化浮點數格式標準:
1. e = 0,且f != 0:單精度浮點數的值為(-1)s×2-126×0.f
2. e = 0,且f = 0:單精度浮點數的值為(-1)s×0
3. e = 255,且f != 0:單精度浮點數的值為NaN(Not a Number),例如∞-∞ = NaN
4. e = 255,且f = 0:單精度浮點數的值為(-1)s×∞
雙精度浮點數格式與單精度浮點數格式定義類似,這里就不再贅述了。
三、參考資料
[1]?李亞民.?計算機原理與設計——Verilog?HDL版.?北京:清華大學出版社.?2011
[2]??fromtitle=IEEE&fromid=150905&type=syn.?2015年02月15日
[3]?.?2015年02月15日
[4]??url=bp2fjdfgSOP8-PJwnDgzUbqqpnKxIq4GOnkKZFWnMqWVlHVi2gAUbSeXV8dy2oVjwQ0AARKgQ9DukmhpFBrXcq.?2015年02月15日
[5]?IEEE.?IEEE?Standard?for?Binary?Floating-Point?Arithmetic.?1985
 電子發燒友App
電子發燒友App











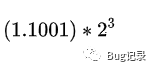


















評論