多用戶環境下陣列響應的閉式盲估計方法
本文通過剖析多徑多用戶環境下陣列輸出信號二階統計量的數據結構,提出了一種基于特征分解的閉式陣列響應盲估計方法.該方法適用于任何幾何形狀的陣列和未校準的陣列,且對信號特性和傳播參數(散射源分布和入射角散布范圍)的約束極少.理論分析與仿真結果表明,該方法能夠有效地進行陣列響應估計和信號分離,在空分多址(SDMA)的實現方面具有較強的實用性.
關鍵詞:陣列天線;盲估計;智能天線;空分多址
Blind Closed-Form Array Response Estimation in Multiuser Scenarios
JIN Liang,WANG Yi-lin,YIN Qin-ye
(Information Engineering Institute,Xi'an Jiaotong University,Xi'an 710049,China)
Abstract:A closed-form array response estimation (CARE) technique for blind source separation in wireless communication is developed by exploiting the data structure of second-order statistics of the array output in the presence of multipath.The proposed method achieves array response estimation with little constraint on signal property and propagation environment such as scatters or angular spread.Moreover,the array considered here can be of arbitrary geometry and even uncalibrated.
Key words:antenna array;blind estimation;smart antenna;SDMA
一、引 言
近年來,為了降低無線通信中的同信道干擾、增加系統容量和提高小區覆蓋范圍,人們開始將陣列天線技術應用于無線基站,所謂的智能天線系統成為目前研究的熱點[1~8].即使在多徑環境下,由于陣列對每個用戶信號的響應各異,因此在同一頻道、同一時隙或同一碼道中的用戶只要空間位置不同就可以通過空域濾波對其進行盲分離[3、4].在時分雙工(TDD)系統中,還可以利用收發信道的互易性,通過上行時估計得到的陣列響應進行下行波束成形,完成下行選擇性發送[5],即保證每個移動用戶只接收到基站發給自己的下行信號而不受同一信道中基站發給其它用戶信號的干擾.顯然,陣列響應中包含了豐富的用戶位置信息,反映了非頻率選擇性衰落環境中用戶與天線陣之間的信道特征,在空分多址(SDMA)的實現方面起著重要作用,所以有時也被稱為用戶的“空間特征(Spatial Signature)”.不僅如此,陣列響應的估計在雷達、聲納等領域也有重要意義.
在傳統方法中均假設陣列響應是到達波方向(DOA)的已知函數,進而可以利用高分辨率DOA估計方法如MUSIC、ESPRIT等進行陣列響應的估計[3,6].然而在多徑條件下信號是相干的,而且DOA與陣列響應之間的關系通常無法確知,因此傳統方法很難適用于實際系統.近來,人們開始利用信號的一些先驗知識如數字通信中的有限碼集(Finite-Alphabet)特性、常用調制方式下的恒模特性等來進行陣列響應估計和信號分離,取得了較好的效果.然而這些方法也存在一些局限,如要求所有信號在碼元上是嚴格同步的[4],或有時會收斂到局部最優點[7]等.另一方面,基于對某些具體應用環境下電磁傳播特性的研究,人們提出了一些近似的信道模型以及相應的陣列響應估計方法,如在用戶本地散射(Local Scattering)模型[8]中假設每組相干信號的DOA分布僅局限于某一很小的角度范圍內.這類方法通常要求陣列是嚴格校準的,并且在多徑DOA散布較大的場合(如微蜂窩和室內無線通信)近似模型并不適用.
本文中重點研究上行信號的陣列響應估計及相關的信號盲分離問題.通過剖析陣列輸出信號二階統計量的數據結構,提出了一種新的閉式陣列響應估計(Closed-form Array Response Estimation)算法,即CARE算法.與上述方法相比,該方法對信號特性和傳播參數(散射源分布和入射角散布范圍)的約束極少,且適用于各種幾何形狀的陣列和未校準的陣列,因此具有較強的實用性.另外,該方法通過特征分解可以得到陣列響應的閉式解,因此計算量較小,穩健性較好,不存在收斂問題.
二、問題的模型
考慮d個窄帶源{sk(t)|k=1,2,…,d}及其多徑信號入射于一個任意的M元天線陣,并假設信道參數和陣列響應在觀測時間內是時不變的.則第i個陣元的輸出為:
![]() (1)
(1)
其中:
Lk是第k個信號sk(t)的多徑數目;
αkl和τkl分別是對應于第l條多徑的衰減和時延;
gi為第i個陣元的復增益,這里假設陣列是未校準的,即gi未知;
ai(θkl)為對應于波達方向角θkl的導向矢量a(θkl)=[a1(θkl),…,ad(θkl)]T的第i個元素(例如對于均勻線陣ai(θkl)=![]() ,其中D為陣元的間距,λ為信號波長);
,其中D為陣元的間距,λ為信號波長);
ni(t)表示均值為零方差為σ2的加性高斯白噪聲,且各陣元間的噪聲互不相關,噪聲與信號互不相關,即:
Rninj(τ)=E{ni(t+τ/2)n*j(t-τ/2)}=σ2.δ(τ)δ(i-j)
Rnisk(τ)=E{ni(t+τ/2)s*k(t-τ/2)}=0 (2)
其中δ(.)為Dirac函數.
這里假定信道為平衰落的(Flat Fading,也稱為非頻率選擇性衰落信道),即多徑造成的時延散布遠小于信號帶寬BWk的例數,
![]()
因此可以利用窄帶條件
sk(t-τkl)=sk(t)ejωcτkl
將陣元輸出表示為:
![]() (3)
(3)
其中aik為信號sk(t)的空間特征ak的第i個元素,
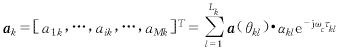 (4)
(4)
上式中ωc為載波頻率.式(3)的矢量形式為:
![]() (5)
(5)
s(t)=[s1(t),…,sd(t)]T,
n(t)=[n1(t),…,nM(t)]T
k被稱為對應于sk(t)的“陣列響應”矢量:
k=[1k,…,ik,…Mk]T,ik=aik.gi (6)
并且A=[1,…,d].在下文中,將討論當s(t)中不含導行信號(Pilot Signal)時如何從唯一的已知條件——陣列輸出x(t)中估計出陣列響應矩陣A.顯然,這是一個全盲估計問題.在估計出A后,可以進一步得到s(t)的估計[2,3],即實現多用戶信號的盲分離.
實際上,從式(5)可以看出,A中的列矢量{1,…,d}張成了整個信號空間,因此可看作是信號空間的原始基底,所以對A的估計實際上是對信號空間原始基底的估計,而且這些基底通常是非正交的.在傳統子空間方法(如MUSIC)中,通過對陣列協方差矩陣的特征值分解我們只能得到信號空間的一組正交基底而不是原始基底,因此直接用傳統方法無法估計陣列響應.在下一節中,將構造一個“特征矩陣(Signature Matrix)”,可以證明,該矩陣非零特征值對應的特征向量即為信號空間的原始基底,從而可以得到陣列響應矩陣A的閉式解.
三、閉式陣列響應估計(CARE)算法
本文選擇陣列中的任意兩個陣元作為“導引陣元(Guiding Sensor)”,不失一般性,假設#1和#2陣元為導引陣元.由于{sk(t)}彼此互不相關,{sk(t)}與ni(t)不相關,且ni(t)為加性高斯白噪聲,根據式(2)、(3)和(6)可以得到一般陣元輸出xi(t)與導引陣元輸出x1(t)的互相關函數如下:
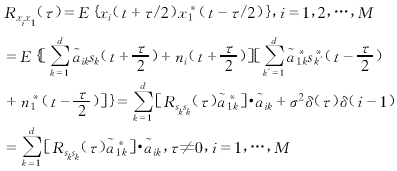 (7)
(7)
其中Rsksk(τ)=E{sk(t+τ/2)s*k(t-τ/2)}.類似地,陣元輸出xi(t)與另一導引陣元輸出x2(t)的互相關函數為:
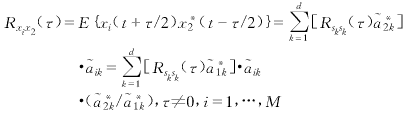 (8)
(8)
式(7)、(8)的矢量形式為:
R1(τ)=ARs(τ) (9)
R2(τ)=AΦRs(τ) (10)
其中 R1(τ)=[Rx1x1(τ),Rx2xl(τ),…,RxMx1(τ)]T
R2(τ)=[Rx1x2(τ),Rx2x2(τ),…,RxMx2(τ)]T
Rs(τ)=[Rs1s1(τ).a*11,Rs2s2(τ).a*21,…,RsDsD(τ).a*D1]T
Φ為對角矩陣:
Φ=diag[a*21/a*11,a*22/a*12,…,a*2d/a*1d]
與對陣列輸出進行快拍類似,對R1(τ),R2(τ)在N個(N>M)τ(τ=Ts,2Ts,…,NTs)上進行均勻采樣,得到“偽快拍”矩陣:
X1=[R1(Ts),R1(2Ts),…,R1(NTs)] (11)
X2=[R2(Ts),R2(2Ts),…,R2(NTs)] (12)
由式(9)、(10)有:
X1=AS,X2=AΦS (13)
其中S=[Rs(Ts),Rs(2Ts),…,Rs(NTs)].由上式可以看出偽快拍矩陣X1和X2與傳統ESPRIT方法[10]及DOA-MATRIX方法[11、12]中的矩陣束在形式上十分相似.但ESPRIT方法只能解出對角陣Φ而無法得到A矩陣.為此,與文獻[11]類似,定義“特征矩陣”如下:
R=X2[X1]- (14)
其中[.]-表示偽逆,即X1[X1]-=I.下列定理給出了本文中陣列響應估計方法的理論基礎.
定理1 若陣列響應矩陣A為滿秩的,則特征矩陣R的d個非零特征值等于矩陣Φ的d個對角元素,這些非零特征值對應的d個特征向量等于矩陣A的d個列矢量,即:
RA=AΦ (15)
證明:由式(13)得到:
S=(AHA)-1AHX1 (16)
將式(16)代回式(13),則x2可表示為:
X2=AΦ(AHA)-1AHX1
所以,RA=X2[X1]-A=AΦ(AHA)-1AHX1[X1]-A=AΦ(AHA)-1AHA=AΦ
證畢
因此,可以通過對矩陣R的特征值分解得到矩陣A的閉式估計,該方法稱為CARE方法.顯然,當陣列具有M個陣元時,CARE方法可以估計出分別對應于M個用戶的M個陣列響應.在得到矩陣A的估計![]() 后,可以有多種方法對這M個用戶信號進行分離和估計,如極大似然(ML)方法:
后,可以有多種方法對這M個用戶信號進行分離和估計,如極大似然(ML)方法:
![]() (17)
(17)
需要指出的是,在陣列響應估計中存在尺度模糊現象,因為
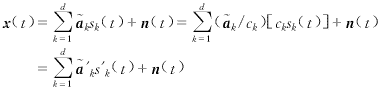
對于任意復常數ck,k和′k均為陣列響應的有效解.然而這種尺度模糊可以通過歸一化的辦法解決,并不影響上行空間濾波和下行波束形成.
綜上,CARE方法的步驟可歸納如下:
(1)選擇陣列中的任意兩個陣元作為導引陣元.
(2)對陣元輸出xi(t)與導引陣元輸出x1(t)、x2(t)的互相關函數Rxix1(τ)、Rxix2(τ)在N個(N>M)τ(τ=Ts,2Ts,…,NTs)上進行均勻采樣,得到式(11)、(12)“偽快拍”矩陣X1和X2.
(3)根據式(14)構造特征矩陣R.
(4)對R進行特征值分解,由上述定理從R的特征向量中得到陣列響應矩陣A.
四、仿真結果
為簡單起見,在仿真實驗中采用陣元數M=7的均勻線陣,盡管CARE方法實際上適用于任意幾何形狀的天線陣.假設線陣是未校準的,因此實驗中隨機選取每個陣元的復增益.進行Nt=100次獨立的Monte-Carlo實驗,在每次實驗中采用100次實際快拍和30次偽快拍.為體現SDMA的特點,各個用戶信號均設為同信道信號,即具有相同的中心頻率(載波).
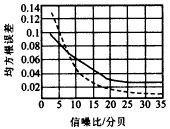
實驗1:假設有d=2個信號源,每個信號源各自有Lk=4條多徑分別從[40°,60°,35°,15°]和[50°,75°,30°,12°]入射,注意這時多徑的DOA散布較大.為定量描述估計的精度,定義陣列響應k(k=1,2)的均方根誤差(RMSE)如下[13]:
![]()
![]() nk為第n次實驗中k的估計.圖1給出了各種信噪比SNR下RMSE的實驗曲線,實線與虛線分別對應1和2估計的RMSE.從中可以看出即使在低信噪比和角度散布較大的情況下CARE方法也能較好的估計k.
nk為第n次實驗中k的估計.圖1給出了各種信噪比SNR下RMSE的實驗曲線,實線與虛線分別對應1和2估計的RMSE.從中可以看出即使在低信噪比和角度散布較大的情況下CARE方法也能較好的估計k.
|
圖1 CARE估計的均方根誤差(RMSE)與信噪比(SNR)的關系.其中實線與虛線分別對應d=2個用戶信號 實驗2:在本實驗中研究CARE方法用于多用戶信號盲估計時的性能,即首先估計出陣列響應,再根據式(17)進行信號分離.假設存在強弱兩個用戶信號,其中信號s1(t)的信噪比SNR=20dB,從DOA為30°、10°的兩條路徑徑入射;另一個信號s2(t)的信噪比SNR=30dB,從DOA為30°+Δθ、10°的兩條路徑入射.兩信號對應路徑的衰減和時延設為相同,即式(1)中的α1l=α2l,τ1l=τ2l(l=1,2).因此,Δθ越小,兩用戶的陣列響應(即空域差異)就越接近,通過空域濾波將兩用戶信號分離的難度就越大.定義信干噪比SINR以度量信號分離的效果,
其中k(t)為信號sk(t)的估計.
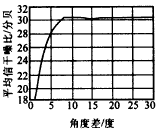
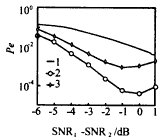
圖2 CARE方法用于兩用戶信號盲估計時的性能曲線.圖中顯示的是兩信號中弱信號的SINR曲線隨Δθ變化的情況 五、結 論 |
 電子發燒友App
電子發燒友App






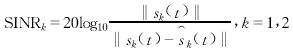




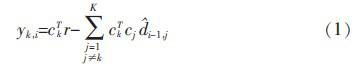














評論