上一篇推文中,我們聊了拉氏變換的物理意義和收斂域,那么單邊拉氏變換、雙邊拉氏變換,有什么區(qū)別和聯(lián)系呢?
2018-06-14 08:51:10 60550
60550 
Z變換和傅里葉變換之間有存在什么樣的關(guān)系呢?傅里葉變換的物理意義非常清晰:將通常在時(shí)域表示的信號,分解為多個正弦信號的疊加。
2019-09-29 07:05:00 5548
5548 1.FFT變換的基本原理 傅立葉變換是數(shù)字信號處理領(lǐng)域一種很重要的算法,可以將一個信號從時(shí)域變換到頻域。傅立葉原理表明:任何連續(xù)測量的時(shí)序或信號,都可以表示為不同頻率的正弦波信號的無限疊加。 根據(jù)
2020-11-09 16:52:40 12476
12476 
UPS是如何把市電的380V交流電變換成逆變器輸出的380V交流電,并在這一變換過程中保持輸出電壓基本不變,是很多數(shù)據(jù)中心UPS用戶經(jīng)常疑惑的問題。
2023-11-04 15:53:10 1286
1286 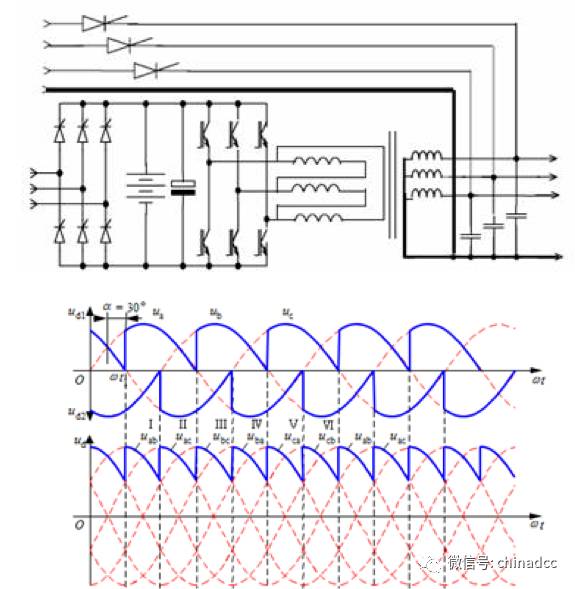
如題,最近在做一個信號與系統(tǒng)的演示程序,但是Z變換這感覺無從下手啊,怎么實(shí)現(xiàn)輸入公式序列然后得到其Z變換的結(jié)果。
2017-04-17 16:42:57
Z變換與拉氏變換、傅氏變換的關(guān)系:一.Z變換與拉氏變換的關(guān)系1.理想抽樣信號的拉氏變換設(shè)為連續(xù)信號, 為其理想抽樣信號,則
2.Z變換與拉氏變換的關(guān)系( S、Z平面映
2009-07-25 10:32:44 40
40
Z變換/Z Transform課件教程:Z變換和傅立葉變換之間的關(guān)系
序列x[n] 的z變換X(z) 為 :
2009-07-25 10:42:50 39
39 1)付里葉變換的四種形式(2)離散付里葉級數(shù)(3)離散付里葉變換(4)離散付里葉變換的有關(guān)性質(zhì)(5)頻率抽樣理論(6)離散付里葉變換的應(yīng)用(7)DFT逼近連
2009-07-25 11:42:30 14
14 快速付里葉變換:一、快速付里葉變換FFT有 限 長 序 列 通 過 離 散 傅 里 葉 變 換 (D F T) 將 其 頻 域 離 散 化 成 有 限 長 序 列 . 但 其 計(jì)算 量 太 大, 很 難 實(shí) 時(shí) 地 處
2009-07-25 11:43:24 76
76 單鍵變換走線層面1. 前言走線中變換層面的快速鍵.2. 說明當(dāng)add connect 命令執(zhí)行中,pop swap將工作層(Act)與變換層對調(diào).subclass top指定工作層(Act)為Top
2009-09-06 11:17:11 0
0 序列的傅里葉變換(DTFT) :DTFT:Discrete-time Fourier transform為研究離散時(shí)間系統(tǒng)的頻率響應(yīng)作準(zhǔn)備,從抽樣信號的傅里葉變換引出:二.傅氏變換、拉氏變換、z變換的關(guān)系1. 三
2009-09-30 19:38:25 0
0 z變換與拉普拉斯變換的關(guān)系:一.z平面與s平面的映射關(guān)系二.z變換與拉式變換表達(dá)式之對應(yīng)
2009-09-30 19:40:36 0
0 反激變換器
基本原理反激變換器斷續(xù)模式反激變換器連續(xù)模式RCC變換器
2010-04-24 08:59:56 29
29 什么是傅里葉變換
傅里葉變換(Transformée de Fourier)是一種積分變換。
因其基本思想首先
2007-11-29 12:46:55 8527
8527 
matlab坐標(biāo)變換
坐標(biāo)變換
cart2pol 笛卡兒坐標(biāo)變換為極坐標(biāo)或圓柱坐標(biāo) cart2sph 笛卡兒坐標(biāo)變換為球坐標(biāo)
2008-06-18 14:47:50 2210
2210 丘克變換器的電壓關(guān)系及Cuk變換器電路拓補(bǔ)結(jié)構(gòu)
2009-05-12 20:54:10 3333
3333 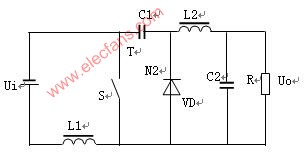
全橋變換器電路
全橋式變換電路當(dāng)S1、S3和S2、S4兩兩輪流導(dǎo)通時(shí),
2009-05-12 21:03:53 3546
3546 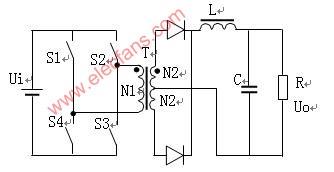
什么是拉普拉斯變換
拉普拉斯變換:拉普拉斯變換(英文:Laplace Transform),是工程數(shù)學(xué)中常用的一種積分變換。如果定義: f(t),是一個關(guān)于t,的函數(shù),使得當(dāng)t<0
2009-07-08 11:42:30 5528
5528 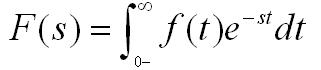
升壓變換器基本電路
圖 升壓變換器基本電路
升壓變換器是將
2009-07-20 16:04:42 1310
1310 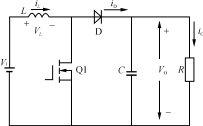
圖 正激型變換電路正激型變換器電路如圖所示,它是采用變壓器耦合的
2009-07-25 08:57:52 1895
1895 Z變換定義:序列x(n)的Z變換定義如下:
Z變換存在的充要條件是上面的
2009-07-25 10:47:58 7633
7633 z變換表
2009-07-25 10:50:00 5900
5900
電光變換原理
2009-07-31 11:52:09 895
895 boost變換器是從BUCK變換器進(jìn)行對偶變換后得到的,其原理如下:
2009-09-23 18:33:42 2784
2784 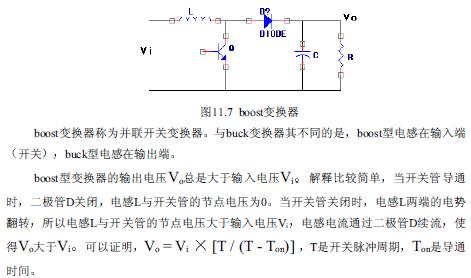
什么是RCC變換器
RCC(RINGING CHOKE CONVERTER)是一種非定頻電源,在國內(nèi)有很多場合應(yīng)用。
RCC變換器的原理
2009-10-12 18:47:51 3474
3474 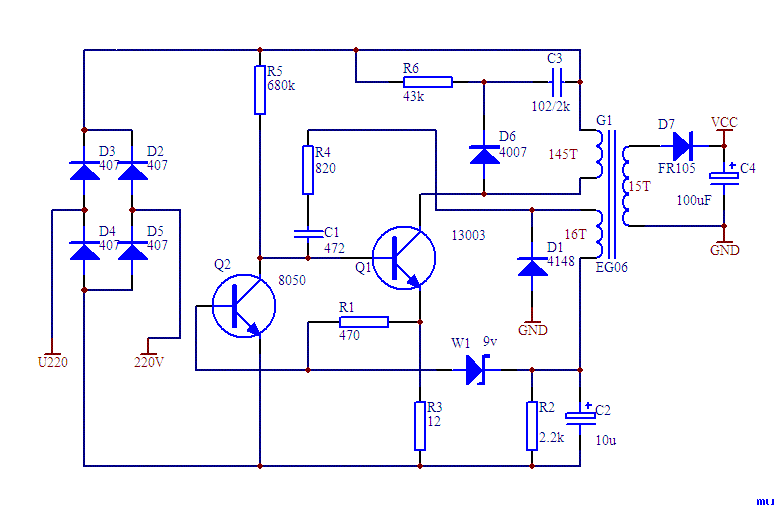
諧振變換器,什么是諧振變換器
諧振變換器由開關(guān)網(wǎng)絡(luò)Ns、諧振槽路NT、整流電路NR、低通濾波器NF等部分組成,其結(jié)構(gòu)框圖由圖1所示。
2009-10-18 10:30:06 10478
10478 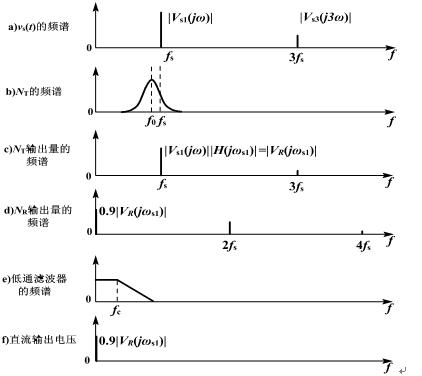
雙輸出SEPIC變換器
雙輸出SEPIC(Single-Ended Primary Inductance Converter- 單端初級電感變換器)變換器電路示于圖1,在此電路中采用Linear公司降壓變換器 LT1767。
2009-11-01 08:42:54 2347
2347 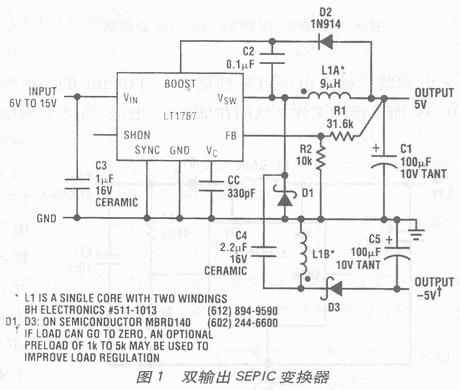
8位串-并變換器電路
串-并變換器是把若干位串行二進(jìn)制編碼變成并行二進(jìn)制編碼的電路。并-串變換器則剛剛相反。
2010-01-12 14:09:07 3411
3411 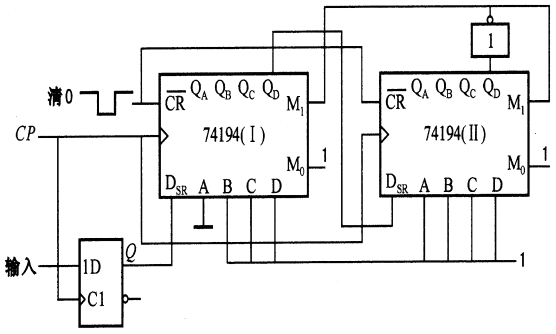
8位并-串變換器
2010-01-12 14:10:04 1661
1661 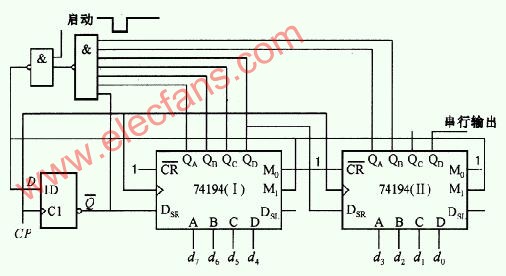
離散傅里葉變換是一種在時(shí)域和頻域均離散的傅里葉變換.
2011-02-23 09:30:10 49
49 對于高頻信號和高頻噪聲干擾相混疊的信號,采用小波變換去除噪聲可以避免用傅里葉變換去噪帶來的信號折損。對于噪聲頻率固定的平穩(wěn)信號,在對信號進(jìn)行傅里葉變換后使用濾波器
2011-03-18 16:47:24 426
426 V/I變換器是一種可以用電壓信號控制輸出電流的電路。兩線制V/I變換器與一般V/I變換電路不同點(diǎn)在:電壓信號不是直接控制輸出電流,而是控制整個電路自身耗電電流
2011-05-11 12:00:46 4385
4385 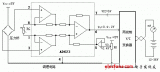
本文介紹了 小波變換 理論, 系統(tǒng)地研究了小波變換在信號處理尤其是信號濾波去噪方面的應(yīng)用。根據(jù)不同類型的噪音, 給出了基于不同小波變換的濾波算法并且基于小波變換的濾波原理
2011-08-03 17:46:46 56
56 傳統(tǒng)的信號理論,是建立在Fourier分析基礎(chǔ)上的,而Fourier變換作為一種全局性的變化,其有一定的局限性。在實(shí)際應(yīng)用中人們開始對Fourier變換進(jìn)行各種改進(jìn),小波分析由此產(chǎn)生了。小波
2011-12-29 10:52:54 121
121 小波變換 金字塔模型 基于變分和小波變換的圖像放大算法
2015-11-24 16:38:42 12
12 時(shí)頻變換工具_(dá)小波變換及其工程應(yīng)用,參考下。
2016-01-15 15:17:24 12
12 (半橋)三電平變換器的優(yōu)點(diǎn)是其開關(guān)管的電壓應(yīng)力為輸人電壓的一半,本文從另一個角度提出它的推導(dǎo)思路,從中提出兩種三電平開關(guān)單元。 將(半橋)三電平變換器的推導(dǎo)思路推廣到所有的直流變換器.提出了三電平
2016-05-11 15:26:21 7
7 本文論述了在基本 DC-DC 開關(guān)變換器中應(yīng)用抽頭扼流圈擴(kuò)展其變換性能,推導(dǎo)了基本關(guān)系式,并對兩種不同型式的變換器的變換性能進(jìn)行了比較。
2016-05-11 15:26:21 5
5 第二章-反z變換
2016-12-28 14:23:30 0
0 Z反變換
2016-12-28 14:23:30 0
0 第3章z變換
2016-12-28 14:23:30 0
0 逆z變換和留數(shù)法
2016-12-28 14:23:30 0
0 反Z變換
2016-12-28 14:23:30 0
0 項(xiàng)目中驗(yàn)證可用的FFT變換傅里葉變換,C語言,帶頭文件。
2017-09-08 20:21:27 15
15 坐標(biāo)變換和矩陣變換的原理放在交流電機(jī)里頭介紹比較容易理解,所以下面介紹的坐標(biāo)變換和變換矩陣都以交流電機(jī)模型來說明。
2017-09-05 10:49:26 329
329 矩陣變換在圖形學(xué)上經(jīng)常用到。基本的常用矩陣變換操作包括平移、縮放、旋轉(zhuǎn)、斜切。每種變換都對應(yīng)一個變換矩陣,通過矩陣乘法,可以把多個變換矩陣相乘得到復(fù)合變換矩陣。
2017-09-06 08:54:16 7
7 深度理解PQ變換與DQ變換
2017-09-14 10:03:58 34
34 為了優(yōu)化雙級矩陣變換器輸出性能,提高其電壓利用率,本文在分析雙級矩陣變換器的拓?fù)浣Y(jié)構(gòu)的基礎(chǔ)上,提出在整流級采用有零矢量的空間矢量調(diào)制策略;在新的調(diào)制策略的思想下,通過對整流級和逆變級的解析變換,推導(dǎo)
2017-11-23 14:39:41 3
3 傅立葉變換,表示能將滿足一定條件的某個函數(shù)表示成三角函數(shù)或者它們的積分的線性組合。在不同的研究領(lǐng)域,傅立葉變換具有多種不同的變體形式,如連續(xù)傅立葉變換和離散傅立葉變換。最初傅立葉分析是作為熱過程的解析分析的工具被提出的。
2017-11-24 10:01:15 23029
23029 
有些情形下一個實(shí)變量函數(shù)在實(shí)數(shù)域中進(jìn)行一些運(yùn)算并不容易,但若將實(shí)變量函數(shù)作拉普拉斯變換,并在復(fù)數(shù)域中作各種運(yùn)算,再將運(yùn)算結(jié)果作拉普拉斯反變換來求得實(shí)數(shù)域中的相應(yīng)結(jié)果,在經(jīng)典控制理論中,對控制系統(tǒng)的分析和綜合,都是建立在拉普拉斯變換的基礎(chǔ)上的。
2017-12-05 18:30:31 247925
247925 
一種積分變換,它來源于函數(shù)的傅里葉積分表示。積分稱為? 的傅里葉積分。拉普拉斯變換是工程數(shù)學(xué)中常用的一種積分變換,又名拉氏變換。拉氏變換是一個線性變換,可將一個有參數(shù)實(shí)數(shù)t(t≥ 0)的函數(shù)轉(zhuǎn)換為一個參數(shù)為復(fù)數(shù)s的函數(shù)。
2017-12-05 19:10:02 85313
85313 
關(guān)于傅里葉變換變換?答:fourier變換是將連續(xù)的時(shí)間域信號轉(zhuǎn)變到頻率域;它可以說是laplace變換的特例,laplace變換是fourier變換的推廣,存在條件比fourier變換
2017-12-25 17:06:49 32133
32133 
本文為大家?guī)韇uck變換器設(shè)計(jì)介紹。
2018-01-10 10:46:28 8509
8509 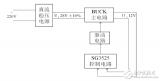
三種灰度變換常用的有圖像反轉(zhuǎn)、對數(shù)變換和伽馬(冪律)變換,灰度變換是指根據(jù)某種目標(biāo)條件按一定變換關(guān)系逐點(diǎn)改變源圖像中每一個像素灰度值的方法。目的是為了改善畫質(zhì),使圖像的顯示效果更加清晰。
2018-01-12 19:22:13 34897
34897 小波變換(wavelet transform,WT)是一種新的變換分析方法,它繼承和發(fā)展了短時(shí)傅立葉變換局部化的思想,同時(shí)又克服了窗口大小不隨頻率變化等缺點(diǎn),能夠提供一個隨頻率改變的“時(shí)間-頻率”窗口,是進(jìn)行信號時(shí)頻分析和處理的理想工具。
2018-01-13 09:42:37 25519
25519 小波變換與傅里葉變換有什么區(qū)別嗎?小波變換與傅里葉變換哪個好?我們通過小波變換與傅里葉變換的詳細(xì)解讀、小波變換與傅里葉變換的區(qū)別、傅里葉變換缺點(diǎn)方面來解析。
2018-01-13 11:02:22 14343
14343 
小波變換(wavelet transform,WT)是一種新的變換分析方法,它繼承和發(fā)展了短時(shí)傅立葉變換局部化的思想,同時(shí)又克服了窗口大小不隨頻率變化等缺點(diǎn),能夠提供一個隨頻率改變的“時(shí)間-頻率”窗口,是進(jìn)行信號時(shí)頻分析和處理的理想工具。
2018-01-15 09:53:07 44373
44373 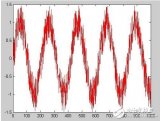
詳細(xì)講述傅里葉變換和小波變換原理
2018-01-16 14:34:42 9
9 文章通過 Buck 變換器推導(dǎo)出移相全橋變換器的小信號電路模型 , 利用解析理論的方法求得變換器運(yùn)行特性的解析表達(dá)式 , 使之成為能對變換器進(jìn)行定性和定量分析的建模方法。
2018-05-30 09:58:21 36
36 大家好,又到了每日學(xué)習(xí)的時(shí)間了,今天我們來聊一聊基于fpga設(shè)計(jì)9/7小波變換原理。 9/7小波變換包括行變換,列變換。 期中行變換包括第一步行變換,第一步行更新,第二步行變換,第二步行更新
2018-08-17 09:52:06 4774
4774 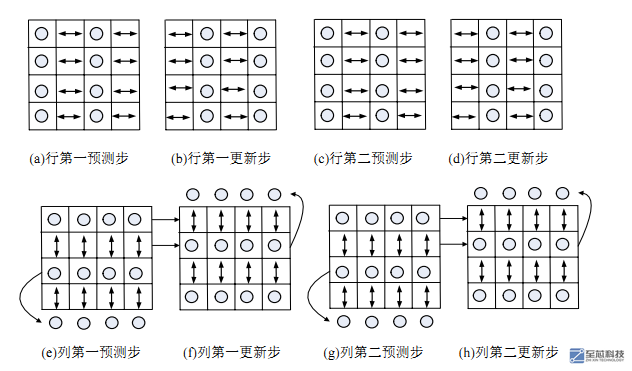
拉普拉斯變換是工程數(shù)學(xué)中常用的一種積分變換,又名拉氏變換。拉氏變換是一個線性變換,可將一個有引數(shù)實(shí)數(shù)t(t≥ 0)的函數(shù)轉(zhuǎn)換為一個引數(shù)為復(fù)數(shù)s的函數(shù)。
2018-09-17 08:02:00 11830
11830 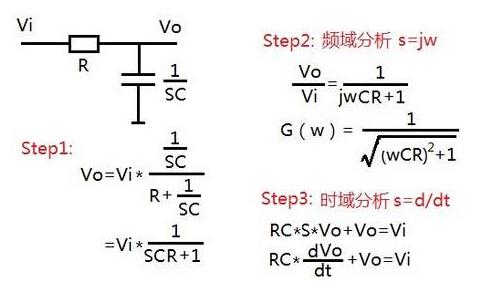
投影就是用一束光線將物體照射后在平面內(nèi)留下的影子,這個影子是物體的一個輪廓。變換指的是傅里葉變換、小波變換等用于分析信號時(shí)頻特性的數(shù)學(xué)工具。變換在工程應(yīng)用中具有非常重要的意義,但其理解往往讓人感覺
2018-11-27 08:00:00 29
29 傅里葉變換是數(shù)字信號處理領(lǐng)城種很重要的算法。傅里葉表明:任何連續(xù)測量的時(shí)序或信號,都可以表示為不同頻率的正弦波信號的無限疊加。而根據(jù)該原理的傅里葉變換算法利用直接測量到的原始信號,以累加方式來計(jì)算
2019-04-30 08:00:00 2
2 opencv的傅里葉變換及逆變換實(shí)現(xiàn)。傅里葉變換需要將數(shù)據(jù)表示為復(fù)數(shù)形式,通過一個兩通道矩陣來記錄復(fù)數(shù)的實(shí)部和虛部,然后通過cvDFT來實(shí)現(xiàn)變換。對于圖片變換也是一樣,只是矩陣換成IplImage格式,用兩個單通道圖片來分別表示實(shí)部和虛部,用兩通道圖片來存放變換結(jié)果。
2019-10-11 14:27:00 3
3 本文檔的主要內(nèi)容詳細(xì)介紹的是如何使用LabVIEW實(shí)現(xiàn)小波變換包括了:小波變換的基本理論,在LabVIEW中實(shí)現(xiàn)小波變換,基于LabVIEW與MATLAB的小波去噪算法實(shí)現(xiàn)
2020-04-20 08:00:00 49
49 在知乎上看到一個問題,傅里葉變換、拉普拉斯變換、Z 變換的聯(lián)系是什么?為什么要進(jìn)行這些變換?我覺得這是一個非常好的問題,貌似一下子也回答不上來,所以整理學(xué)習(xí)并分享一下。
2021-02-15 11:59:00 8430
8430 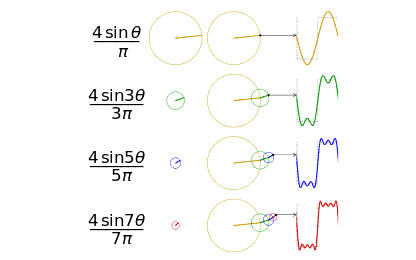
數(shù)學(xué)變換是指數(shù)學(xué)函數(shù)從原向量空間在自身函數(shù)空間變換,或映射到另一個函數(shù)空間,或?qū)τ诩蟈到其自身(比如線性變換)或從X到另一個集合Y的可逆變換函數(shù)。
2021-01-18 16:13:41 3205
3205 
1 hilbert變換 希爾伯特變換是以著名數(shù)學(xué)家大衛(wèi)·希爾伯特(David Hilbert)來命名。在數(shù)學(xué)與信號處理的領(lǐng)域中,一個實(shí)值函數(shù)的希爾伯特變換(Hilbert transform
2021-06-04 15:08:53 26702
26702 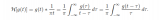
從傅里葉級數(shù)、傅里葉變換推出拉普拉斯變換。
2021-06-23 16:25:27 6160
6160 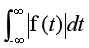
雙向DC變換電源設(shè)計(jì)(監(jiān)控電源最低工作溫度)-雙向DC變換電源設(shè)計(jì)雙向DC變換電源設(shè)計(jì)雙向DC變換電源設(shè)計(jì)
2021-07-26 14:10:28 34
34 關(guān)于傅立葉變換,無論是書本還是在網(wǎng)上可以很容易找到關(guān)于傅立葉變換的描述,但是大都讓人很難理解太過抽象,盡是一些讓人看了就望而生畏的公式的羅列。 要理解傅立葉變換,確實(shí)需要一定的耐心,別一下子想著
2021-08-25 11:25:24 4202
4202 數(shù)學(xué)變換是指數(shù)學(xué)函數(shù)從原向量空間在自身函數(shù)空間變換,或映射到另一個函數(shù)空間,或?qū)τ诩蟈到其自身(比如線性變換)或從X到另一個集合Y的可逆變換函數(shù)。
2022-07-23 17:45:10 2181
2181 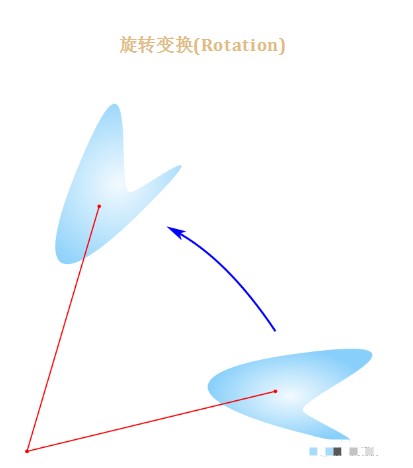
傅里葉變化只能對能量有限的信號進(jìn)行變換(也就是可以收斂的信號),無法對能量無限的信號進(jìn)行變換(無法收斂),因此,拉普拉斯應(yīng)運(yùn)而生,在原先的傅里葉變換公式中乘以一個衰減因子,使得無限能量的信號也能進(jìn)行時(shí)頻變換。
2022-11-28 11:00:23 1564
1564 在正式進(jìn)入小波變換之前,我們不妨來討論一下傅里葉變換的局限性和為什么我們需要引入小波變換。
2023-06-27 11:30:48 699
699 
磁場定向控制中使用到的坐標(biāo)變換主要有Clark變換、Park變換、Anti-Park變換。
2023-07-07 15:41:42 1189
1189 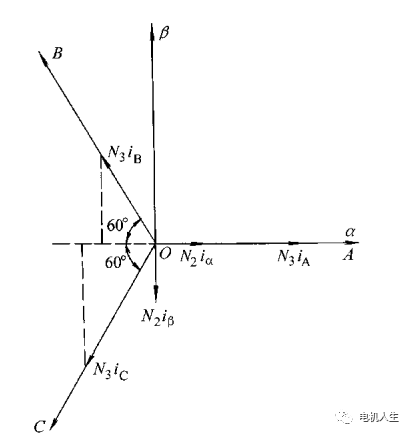
本文主要給定一小段音頻,通過短時(shí)傅里葉變換和小波變換制作時(shí)頻圖。音頻的采樣率為44100
2023-07-19 17:44:25 1069
1069 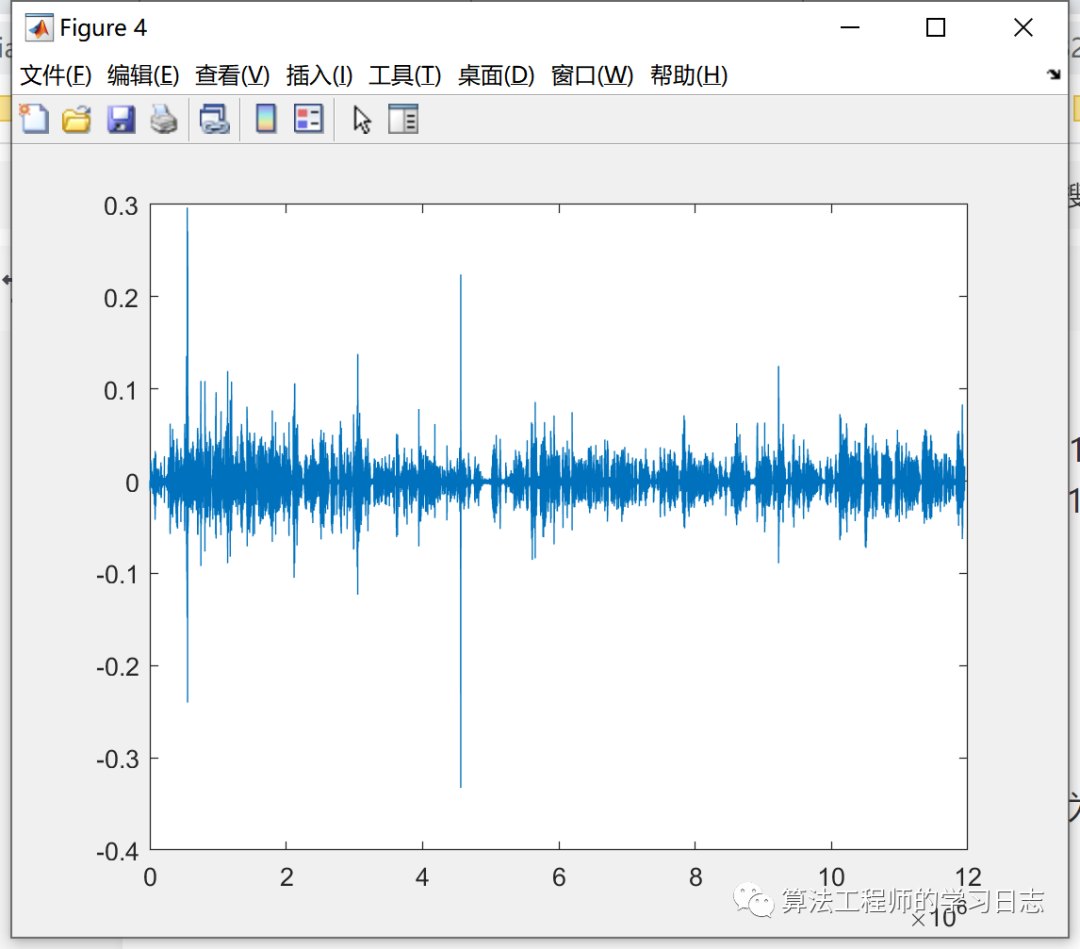
傅里葉變換十大公式 傅里葉變換的十大性質(zhì)? 傅里葉變換是一種重要的數(shù)學(xué)工具,在許多領(lǐng)域中都有廣泛的應(yīng)用。傅里葉變換可以將一個時(shí)域信號轉(zhuǎn)化為頻域信號,分析不同頻率成分在信號中的占比情況。由于傅里葉變換
2023-09-07 16:14:36 8619
8619 傅里葉變換基本性質(zhì) 傅里葉變換本質(zhì) 傅里葉變換的應(yīng)用 傅里葉變換是現(xiàn)代數(shù)學(xué)、物理學(xué)、工程學(xué)等領(lǐng)域中非常重要的一種數(shù)學(xué)工具和基本理論。在信號處理、圖像處理、通信技術(shù)、音樂分析、光學(xué)、醫(yī)學(xué)、天氣預(yù)報(bào)
2023-09-07 16:18:49 5494
5494 傅氏變換和傅里葉變換的區(qū)別聯(lián)系 傅氏變換和傅里葉變換是信號處理中常用的兩種變換方法,它們有著不同的作用和特點(diǎn)。傅氏變換主要應(yīng)用于連續(xù)時(shí)間信號的頻域分析,而傅里葉變換則主要用于離散時(shí)間信號的頻域分析
2023-09-07 16:35:05 863
863 傅里葉變換拉普拉斯變換和z變換的區(qū)別聯(lián)系 傅里葉變換、拉普拉斯變換和z變換是信號處理中重要的數(shù)學(xué)工具。傅里葉變換用于將一個連續(xù)時(shí)間信號轉(zhuǎn)換為頻域表示;拉普拉斯變換則用于將一個連續(xù)時(shí)間信號轉(zhuǎn)換為復(fù)平面
2023-09-07 16:38:58 1408
1408 傅里葉變換和傅里葉逆變換的關(guān)系? 傅里葉變換和傅里葉逆變換是信號處理領(lǐng)域中極具重要性的數(shù)學(xué)工具,它們被廣泛應(yīng)用于很多領(lǐng)域,例如音頻、圖像處理、通信等。 傅里葉變換是將一個信號在時(shí)域(即時(shí)間或空間
2023-09-07 16:43:47 3080
3080 傅里葉變換和反變換公式? 傅里葉變換和反變換在信號處理領(lǐng)域中被廣泛應(yīng)用。傅里葉變換是將一個時(shí)域信號轉(zhuǎn)換為頻域信號的過程,而傅里葉反變換則是將一個頻域信號轉(zhuǎn)換為時(shí)域信號的過程。這篇文章將詳細(xì)講解
2023-09-07 16:53:04 9123
9123 傅里葉變換公式理解 傅里葉變換是一種在數(shù)學(xué)、物理、工程和其他科學(xué)領(lǐng)域中常用的工具,它是一種將一個函數(shù)從時(shí)域轉(zhuǎn)換到頻域的方法。傅里葉變換可以將一個復(fù)雜的函數(shù)表示成一個頻域上各種周期函數(shù)的疊加,從而
2023-09-07 16:53:06 2625
2625 為什么有四種形式的傅里葉變換? 傅里葉變換是一種十分重要的數(shù)學(xué)工具,它可以將函數(shù)從時(shí)域(即時(shí)間域)轉(zhuǎn)換到頻域,從而能夠幫助人們更好地理解信號的特性。在傅里葉變換的研究過程中,出現(xiàn)了幾種不同的變形方式
2023-09-07 17:04:04 838
838 小波變換與傅里葉變換的區(qū)別和聯(lián)系? 1. 傅里葉變換和小波變換的定義 傅里葉變換(Fourier Transform,簡稱FT)是一種將信號在時(shí)域上的函數(shù)轉(zhuǎn)變?yōu)轭l域上的函數(shù)的方法,對于連續(xù)時(shí)間信號
2023-09-07 17:04:07 1636
1636 如何由傅里葉變換推出傅里葉反變換? 傅里葉變換和傅里葉反變換是信號處理和通信領(lǐng)域中的兩個重要概念,是數(shù)字信號和連續(xù)信號的重要數(shù)學(xué)分析方法之一。傅里葉變換可以將時(shí)間域信號轉(zhuǎn)化為頻率域信號
2023-09-07 17:04:09 1267
1267 短時(shí)傅里葉變換和小波變換差別 短時(shí)傅里葉變換(short-time Fourier transform,STFT)和小波變換(wavelet transform)是兩種常見的信號處理技術(shù),它們在頻域
2023-09-07 17:04:12 1547
1547 傅里葉變換和離散傅里葉變換的關(guān)系 傅里葉變換(Fourier Transform)是一種將時(shí)間域(或空間域)的信號轉(zhuǎn)換為頻率域(或波數(shù)域)的信號的數(shù)學(xué)工具。而離散傅里葉變換(Discrete
2023-09-07 17:04:15 1419
1419 小波變換是如何定義的? 小波變換是一種多尺度分析方法,它可以將信號分解成不同頻率下的小波基函數(shù)。小波基函數(shù)可以表示信號的局部特征,如局部振幅和頻率,而且可以提供更好的時(shí)頻局部化信息。小波變換不同于
2023-09-07 17:04:17 1135
1135 傅里葉變換的定義 傅里葉變換的意義? 傅里葉變換,表示能將滿足一定條件的某個函數(shù)表示成三角函數(shù)(正弦和/或余弦函數(shù))或者它們的積分的線性組合。 在不同的研究領(lǐng)域,傅里葉變換具有多種不同的變體
2023-11-30 15:32:49 731
731 傅里葉變換和拉普拉斯變換是兩種重要的數(shù)學(xué)工具,常用于信號分析和系統(tǒng)理論領(lǐng)域。雖然它們在數(shù)學(xué)定義和應(yīng)用上有所差異,但它們之間存在緊密的聯(lián)系和相互依存的關(guān)系。 首先,我們先介紹一下傅里葉變換和拉普拉斯
2024-02-18 15:45:38 344
344
 電子發(fā)燒友App
電子發(fā)燒友App

 硬聲App
硬聲App

 60550
60550
 5548
5548 12476
12476
 1286
1286
 40
40 39
39 14
14 76
76 0
0 0
0 0
0 2210
2210 3333
3333
 5528
5528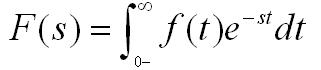
 3474
3474
 10478
10478
 2347
2347
 426
426 4385
4385
 56
56 121
121 7
7 5
5 329
329 7
7 3
3 23029
23029
 247925
247925
 85313
85313
 32133
32133
 34897
34897 25519
25519 14343
14343
 44373
44373
 36
36 4774
4774
 11830
11830
 29
29 2
2 3
3 49
49 8430
8430
 3205
3205
 26702
26702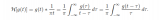
 34
34 4202
4202 2181
2181
 1564
1564 1189
1189
 1069
1069
 8619
8619 5494
5494 863
863 1408
1408 3080
3080 9123
9123 2625
2625 838
838 1636
1636 1267
1267 1547
1547 1419
1419 1135
1135 731
731 344
344
評論